אינטרפרומטר פברי-פרו
אינטרפרומטר פברי-פרו (מכונה לעיתים "אטלון") הוא מכשיר אופטי המורכב משני מישורים (מראות) מקבילים, בעלי מקדמי החזרה גבוהים, הממוקמים במרחק קטן זה מזה.
המישורים יכולים להיות ממוקמים במרחק d אחד מהשני, הנע באופן טיפוסי בין מספר מילימטרים למספר סנטימטרים בודדים. אם המרווח d יכול להשתנות על ידי תזוזה מכנית של אחת המראות, אזי זהו האינטרפרומטר; אך אם זוג המראות המקבילות מקובעות במקום, מכונה המכשיר בשם "אטלון".
מכשיר זה נבנה לראשונה על ידי שארל פברי ואלפרד פרו בסוף המאה ה-19. מלבד היותו מכשיר המשמש לספקטרוסקופיה עם כושר הפרדה גבוה (נתח תדרים), הוא משמש גם כחלל תהודה עבור הלייזר הבסיסי (מהוד אופטי).
תיאור כללי[עריכת קוד מקור | עריכה]

אינטרפרומטריה היא תחום המתבסס על תופעת ההתאבכות בין גלים. תבנית ההתאבכות נוצרת למשל על ידי פיצול קרן אור אחת לשתי אלומות אור כאשר כל אחת מהן עוברת דרך אופטית שונה ואיחוד הקרניים המפוצלות חזרה.
מהוד אופטי (אינטרפרומטר) מורכב מזוג מראות מישוריות מקבילות המחזירות חלקית והמרוחקות במרחק של מילימטרים עד סנטימטרים בודדים זו מזו. ההארה מושגת על ידי הצבת מקור אור נקודתי במישור מוקד של עדשה מרכזת הגורמת לקרני האור להיות מקבילות זו לזו. לאחר מכן קרני האור עוברות דרך המהוד האופטי ודרך עדשה מרכזת לקבלת תבנית ההתאבכות הנוצרת בצורת טבעות מעגליות. חדות הטבעות הללו תלויה במידת ההחזרה של המראות המישוריות במהוד, ככל שמידת ההחזרה גבוהה יותר כך החדות ויכולת ההבחנה בין טבעות ההתאבכות גבוהה יותר.
יישומים[עריכת קוד מקור | עריכה]
- פילטרים דו צבעיים בנויים ממערך של סדרת אינטרפרומטרים (אטלון) על משטח אופטי. לפילטרים הללו לרוב יש פסי העברה והחזרה מדויקים יותר מאשר לפילטרים אחרים בעלי יכולת בליעה. בתכנון נכון, הפילטרים הדו-צבעיים יכולים להחזיר אורכי גל לא רצויים ולכן הם בעלי יתרון על פני פילטרים בעלי יכולת בליעה. השימוש בפילטרים דו-צבעיים הוא נרחב, ומצוי במכשור אופטי רב כגון מקורות אור, מצלמות, ציוד אסטרונומי ומערכות לייזר.
- מכשירי מדידה אופטיים עושים שימוש באינטרפרומטרי פברי פרו בעלי תחום ספקטרלי חופשי (Free Spectral Range) מסוגלים לקבוע את אורך הגל של האור בדיוק רב.
- מהודי לייזר מתוארים לרוב כמהוד פברי פרו, על אף שלרוב אחת המראות של מהוד הלייזר היא מראה מחזירה באופן מלא (100% החזרה).
- אטלונים המצויים במהודי לייזר משמשים לרוב ליצירת לייזרים חדי אופן.
- ניתן לעשות שימוש באינטרפרומטר פברי פרו ליצירת ספקטרומטר המסוגל להבחין באפקט זימן, כאשר הקווים הספקטראליים בספקטרומטר רגיל קרובים מדי ולא ניתנים להבחנה.
- באסטרונומיה עושים שימוש באטלון כדי לברור מעבר אטומי יחיד בהדמיה, למשל המעברים H-alpha בשמש ו-Ca-K בשמש.
- בזיהוי גלי כבידה נעשה שימוש במהוד פברי פרו על מנת לשמור את הפוטונים במשך כמילי-שנייה אחת בין שתי המראות, ובמשך זמן זה וניתן להבחין בתגובה בין גלי הכבידה לגלי האור.
מהלך הקרניים[עריכת קוד מקור | עריכה]

קרן אור (גל אלקטרומגנטי) נכנסת לאינטרפרומטר ומתקדמת ימינה לאורך ציר המהוד.
חלק מהקרן מועבר החוצה דרך מראה 2 וחלק אחר מוחזר ממראה 2 ומתקדם חזרה למראה 1, ומשם מוחזר שוב לכיוון מראה 2 וחוזר חלילה (איור 1).
כתוצאה מכך מתקבלות קרניים מקבילות ביציאה מהאינטרפרומטר, שאותן ניתן לרכז באמצעות עדשה, ולקבל את תבנית ההתאבכות.
המערכת נמצאת באוויר: , וכמו כן מחוק שימור האנרגיה מתקיים: , כאשר , הם מקדמי החזרת השדה והעברת השדה בהתאמה.
מייצג את הפסדי האנרגיה שלרוב ניתנים להזנחה, הפסדים אלו נגרמים כתוצאה מהפסדי בליעה לפי חוק בר-למברט וכתוצאה מפיזורים וכתוצאה מהפסדי עקיפה הנגרמים בגלל חוסר האידיאליות של המראות וגודלם הפיזי המוגבל.
עבור מצב בו אין הפסדי אנרגיה נקבל: . נוכל תמיד להתייחס אל מקדמי ההחזרה כממשיים חיוביים.
השדה של הגל האלקטרו-מגנטי[עריכת קוד מקור | עריכה]
השדה הנכנס הוא , כאשר הוא התדר הזמני של הגל המתקדם, ובאופן כללי .
השדה השקול במוצא נתון על ידי חיבור סקלארי של השדות החלקיים העוברים: .
לפי סכום סדרה הנדסית נקבל:
כאשר הוא וקטור הגל, וגודלו .
מקדם העברת ההספק[עריכת קוד מקור | עריכה]
היחס בין העוצמה העוברת לבין העוצמה הפוגעת, כלומר מקדם העברת ההספק, הוא:
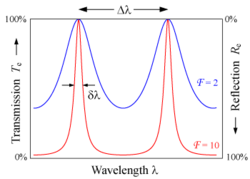
נגדיר: וכמו כן נגדיר את מקדם העידון (Finesse): ונקבל:
העברת הספק מקסימלית תתרחש כאשר יתקיים:
,כאשר מספר ממשי שלם.
כלומר כאשר המרחק בין המראות הוא כפולה שלמה של חצי אורך גל מתקבל רזוננס (כלומר כל הגלים היוצאים באותו כיוון בעלי אותה פאזה).
העברת הספק מינימלית תתרחש כאשר יתקיים :

לעיתים נוח להשתמש במונחים של התדר האופטי ולכן נגדיר: ,כאשר הוא מקדם השבירה.
אז ניתן לרשום:
ונקבל:
לפיכך קיבלנו כי , נקרא גם (Free Spectral Range (FSR, הוא המחזור של .
מקסימום מתקבל עבור כאשר הוא מספר ממשי שלם
ומינימום מתקבל עבור .
חצאי הגובה המקסימלי יתקבלו עבור .
עבור נקבל: , לכן נקבל שמלוא הרוחב בחצי הגובה הוא:
עוצמת האור העובר תלויה בפאזה היחסית הנוצרת בין הגלים היוצאים ומשפיעה על ההתאבכות ביניהם. הפאזה היחסית הזו פרופורציונית לתדר האופטי . העוצמה היא פונקציה מחזורית של , ומקבלת ערך מקסימום כאשר . ככל שמקדם העידון גבוה יותר כך מקבלים פיקים צרים יותר וסף מינימום נמוך יותר. כך ניתן להשתמש באינטרפרומטר פברי פרו לצורך פילטר צר סרט.
כניסת האור בזווית וכושר הפרדה כרומטי[עריכת קוד מקור | עריכה]
כאשר מקור ההארה רחב והקרניים נכנסות בזווית אל האינטרפרומטר (אטלון) אז נוצרות תבניות התאבכות טבעתיות המאפשרות יכולת הפרדה כרומטית עבור אורכי גל שונים. לרוב משתמשים בעדשות לפני המהוד ולאחריו, על מנת שהקרניים היוצאות יתמקדו באזור מסוים.
התנאי למקסימה בהעברה הוא: , וכל הנקודות המצויות על המעגל מקיימות אותו. כאשר מקור האור אינו מונוכרומטי נוצרת מערכת של מעגלי התאבכות לכל אורך גל בנפרד, ויהיה ניתן להבחין בין שתי טבעות התאבכות בסדר השייכות לאורכי גל שונים אם הן רחוקות אחת מהשנייה כך שלפחות הן משיקות החל ממחצית מעוצמתן:
נגדיר: ונקבל, בדומה לפיתוח הקודם:
לכן מקדם העברת ההספק, כלומר היחס בין העוצמה העוברת לעוצמה הפוגעת יהיה:
כאשר נגדיר בשנית ונניח שימור אנרגיה ללא בליעה נוכל לרשום:
הגודל מוגדר כפונקציית איירי (Airy function) ומייצג למעשה את העוצמה העוברת היחסית. ניתן לראות כי נקודות המקסימום מתקבלות עבור ,
כלומר כאשר: ,
והן הולכות ונעשות צרות יותר ככל ש- גדל, כלומר גדל.
כושר ההפרדה הכרומטי (Chromatic Resolving Power) מוגדר לפי: וניתן לראות כי ככל שמקדמי ההחזרה גדלים כך משתפרת הרזולוציה הכרומטית, כיוון שהטבעות נעשות צרות יותר, אך יחד עם זאת עוצמת האור העובר נחלשת.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Eugene Hecht, OPTICS Fourth Edition, Addison Wesley-Pearson Education, 2002
- Bahaa E. A. Saleh, Malvin Carl Teich, Fundamentals of Photonics, A Wiley-Interscience Publication - John Wiley & Sons, INC, 1991







![{\displaystyle E_{in}=U_{in}\exp[jwt]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e39861c8c90a7588386c9c5ef15813774f56e9d)


![{\displaystyle E_{out}=\left[\sum _{i=0}^{\infty }U_{out,i}\right]\exp[jwt]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2af7153c8b333cee9b81c83c7130a1438dd50f76)
![{\displaystyle U_{out}=\sum _{R}U_{R}=\left[t_{1}t_{2}\exp[-jkd]+t_{1}t_{2}\exp[-jkd]r_{1}r_{2}\exp[-2jkd]+...\right]U_{in}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d0b8575d69c5830f9c2571acd2af6827d86342c)
![{\displaystyle U_{out}={\frac {t_{1}t_{2}\exp[-jkd]}{1-r_{1}r_{2}\exp[-2jkd]}}U_{in}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2765acd9f9aab6175b3e7cff741ec69758f3063c)


![{\displaystyle T_{out}=\left|{\frac {U_{out}}{U_{in}}}\right|^{2}={\frac {I_{t}}{I_{i}}}={\frac {|t_{1}|^{2}|t_{2}|^{2}}{|1-r_{1}r_{2}exp[-2jkd]|^{2}}}={\frac {|t_{1}|^{2}|t_{2}|^{2}}{\left[1+{\frac {4r_{1}r_{2}\sin ^{2}(kd)}{(1-r_{1}r_{2})^{2}}}\right](1-r_{1}r_{2})^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdbe2598b75bebe2156fe81ce1a4b350be11823d)


^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16bdf97e1d9741c43d4de3e29b172069ea33acb3)










^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0382481794225db1f4080fd725c023e8495b27b)















![{\displaystyle \left|{\frac {U_{out}}{U_{in}}}\right|=\left|{\frac {t_{1}t_{2}}{1-r_{1}r_{2}\exp[-j\delta ]}}\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f3395d7473216ef66e8e563dfa9120e7406c09c)





![{\displaystyle [1+F\sin ^{2}({\frac {\delta }{2}})]^{-1}\equiv A(\theta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d3a92669f274c0ee3910b409f373c4626f1e660)




