בנייה בסרגל ובמחוגה


בגאומטריה האוקלידית של המישור, בנייה בסרגל ובמחוגה היא בנייה של עצמים גאומטריים, כגון קטעים בעלי תכונות מוגדרות, הנעזרת בסרגל ובמחוגה בלבד. לעניין זה, הסרגל והמחוגה אינם הכלים הפיזיים המשמשים בשרטוט, אלא הפשטות גאומטריות, המממשות את שלוש האקסיומות הראשונות מבין חמש האקסיומות של אוקלידס בספרו "יסודות":
- הסרגל הגאומטרי הוא כלי, המאפשר יצירת קו ישר או קטע ארוך כרצוננו, העובר דרך שתי נקודות נתונות. הסרגל אינו מכויל ואינו בעל יכולת מדידה (לא מסומנות עליו שנתות, המציינות יחידות אורך), וההנחה היא שאי-אפשר ליצור עם הסרגל לבדו שני ישרים מקבילים במרחק נתון זה מזה.
- המחוגה הגאומטרית מאפשרת להתוות מעגל, שמרכזו הוא נקודה נתונה, ורדיוסו נתון או שווה למרחק בינה לבין נקודה אחרת.
אוינופידיס היה הראשון שהתחיל לחקור את הנושא.
פעולות אפשריות[עריכת קוד מקור | עריכה]
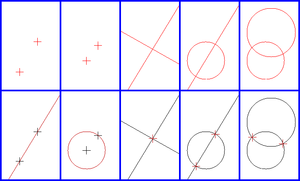
סרגל ומחוגה מאפשרים לבצע שתי פעולות יסודיות:
- שרטוט ישר (ארוך כרצוננו) שעובר דרך שתי נקודות נתונות
- שרטוט מעגל שמרכזו בנקודה נתונה, והוא עובר דרך נקודה נתונה אחרת.
בנוסף לזה אפשר למצוא את:
- נקודת החיתוך של שני ישרים (שאינם מקבילים)
- נקודות החיתוך של ישר ומעגל (אם קיימות)
- נקודות החיתוך של שני מעגלים (אם קיימות)
בניה במחוגה וסרגל היא שרשרת של פעולות כאלו, המגיעה אל התוצאה המבוקשת.
דוגמאות לבניות פשוטות[עריכת קוד מקור | עריכה]

ניתן לבנות בעזרת הסרגל והמחוגה בניות רבות ומגוונות. דוגמאות לבעיות בנייה אלמנטריות:
- בניית אנך אמצעי לקטע: משרטטים שני מעגלים שמרכזיהם קצות הקטע ורדיוסיהם גדולים מאורך חצי הקטע ושווים זה לזה. מעבירים ישר דרך נקודות החיתוך של המעגלים וזהו האנך האמצעי.
- בניית אנך לישר דרך נקודה נתונה על הישר או מחוצה לו: משרטטים מעגל שמרכזו הנקודה הנתונה והוא חותך את הישר. האנך האמצעי לקטע שנקודות החיתוך מקצות הוא האנך המבוקש.
- העברת ישר מקביל לישר נתון, דרך נקודה שמחוץ לישר: מעבירים אנך לישר דרך הנקודה, ולאחר מכן אנך נוסף לאנך דרך הנקודה.
- הקצאת קטע על ישר (כלומר - מציאת נקודה על ישר L שמרחקה מנקודה A שעל הישר שווה למרחק בין שתי נקודות C ו- D)
- הקצאת זווית (כלומר, בהינתן הנקודות A,B,C,D,E, מציאת נקודה X כך שהזווית ABX שווה לזווית CDE)
- בניית חוצה זווית (כלומר חלוקת זווית נתונה לשתי זוויות שוות): מעבירים מעגל כלשהו שמרכזו בקודקוד הזווית, מחברים את נקודות החיתוך של המעגל עם שוקי הזווית ומעבירים לקטע שנוצר אנך אמצעי.
- בניית משולש שנתונים אורכי צלעותיו: משרטטים את אחת הצלעות, ומעבירים שני מעגלים שמרכזיהם בקצות הצלע ורדיוסיהם שווים לאורך שתי הצלעות האחרות. מחברים את קצות הקטע עם אחת מנקודות החיתוך של המעגלים ונוצר המשולש המבוקש.
- בניית מעגל חוסם למשולש (כלומר מעגל העובר דרך שלושת קודקודי המשולש): בונים אנכים אמצעיים לשתיים מצלעות המשולש. נקודת החיתוך שלהם היא מרכז המעגל, ומרחקה מהקודקודים זהו הרדיוס.
- בניית מעגל חסום במשולש (כלומר מעגל המשיק לכל צלעות המשולש): בונים חוצי זווית לשתיים מזוויות המשולש. נקודת החיתוך שלהם היא מרכז המעגל. בונים ממנה אנך לאחת הצלעות ואורכו הוא רדיוס המעגל.
פעולות נפוצות נוספות הן: חיבור וחיסור של אורכי קטעים, כפל וחילוק שלהם במספרים רציונליים, חיבור וחיסור זוויות ועוד.
בעיות בנייה מפורסמות[עריכת קוד מקור | עריכה]
פרט לבעיות הקלות שנמנו בסעיף הקודם, בעיות בנייה היו אחד הכוחות שהניעו את התקדמות הגאומטריה לאורך השנים. בין הבעיות הנודעות יותר נמנות:
- בעיית אפולוניוס: להעביר מעגל שישיק לשלושה מעגלים נתונים. בעיה זו הוצגה על ידי אפולוניוס מפרגה, 260-170 לפני הספירה, שספרו "חתכי חרוט" פרץ דרכים חדשות בגאומטריה שמעבר לישרים ומעגלים. אפולוניוס פתר, ככל-הנראה, את הבעיה, אלא שפתרונו (בספר De Tactionbus) אבד. הבעיה נפתרה על ידי פרנסואה וייט, המתמטיקאי הצרפתי בן המאה השש-עשרה, ואחר-כך, בדרכים פשוטות יותר, על ידי אחרים, בהם על ידי גאוס.
- בעיית הביליארד של אל-חסן: לחסום משולש שווה-צלעות במעגל נתון, באופן ששתיים מצלעות המשולש יעברו דרך נקודות נתונות. הבעיה הוצגה על ידי המתמטיקאי הערבי אבן אל-היית'ם, שחי בין השנים 965 ל-1039, לערך, וכתב ספר חשוב באופטיקה. בעיה זו אפשר לנסח גם כך: מצא, על מעגל נתון, את הנקודה שסכום מרחקיה משתי נקודות נתונות הוא הקטן ביותר. את הבעיה פתר אל-חסן, עקרונית, על ידי חיתוך המעגל הנתון עם היפרבולה מתאימה.

- בעיית קסטיליון, המבקשת להעביר משולש החסום במעגל נתון דרך שלוש נקודות נתונות. הבעיה הוצגה על ידי גבריאל קרמר, ונפתרה ב-1776 על ידי G.F. Salvemini, שנטל לעצמו את השם קסטיליון על-שם מקום הולדתו בעיירה קסטיליון פלורנטינו שבחבל טוסקנה.
- בעיית מלפאטי: לשרטט במשולש נתון, שלושה מעגלים שיהיו משיקים לצלעות המשולש ומשיקים זה לזה. את הבעיה הציג ופתר המתמטיקאי האיטלקי ג'אן פרנצ'סקו מלפאטי (אנ'), 1731-1807.
- בעיית מונג: בהינתן שלושה מעגלים, למצוא מעגל החוצה את שלושתם בניצב. בעיה זו הוצגה על ידי הצרפתי Monge, 1746-1818. כדי לפתור בעיה זו, הראה מונג שהמקום הגאומטרי של מרכזי המעגלים החוצים בניצב שני מעגלים נתונים, הוא קו ישר.
הבעיות הגאומטריות של ימי קדם[עריכת קוד מקור | עריכה]
 ערך מורחב – הבעיות הגאומטריות של ימי קדם
ערך מורחב – הבעיות הגאומטריות של ימי קדם
היוונים הקדמונים ניסחו ארבע בעיות, אשר במשך כ-2,000 שנה היו בעיות פתוחות:
- הכפלת הקובייה: בניית קובייה שנפחה כפול מהנפח של קובייה נתונה
- תרבוע המעגל: בניית ריבוע השווה בשטחו למעגל נתון
- שילוש זווית: חלוקת זווית נתונה לשלושה חלקים שווים
- בנייה של משובע משוכלל
כל ארבע הבעיות הוכחו כבלתי פתירות, באמצעות יישום אלמנטרי של התורה המתמטית העוסקת בהרחבת שדות.
בניית מצולעים[עריכת קוד מקור | עריכה]
 ערך מורחב – מצולע בר-בנייה
ערך מורחב – מצולע בר-בנייה
כדי לבנות מצולע משוכלל בן n צלעות, צריך לבנות את הזווית בת מעלות, כלומר לבנות קטע שאורכו . מספר זה נמצא בתוך שדה ההרחבה מעל הרציונליים של שורש היחידה מסדר n, המכונה גם השדה הציקלוטומי ה-n-י. גאוס הוכיח באמצעות השיטות של תורת גלואה ומחקריו על שורשי יחידה, שאפשר לבנות מצולעים משוכללים שמספר הצלעות שלהם הוא מכפלה של חזקת 2 וראשוני פרמה שונים. בפרט אפשר לבנות את המצולע המשוכלל בן 17 צלעות (גאוס הציג בנייה אלגברית מפורשת למצולע כזה ב-1801), ואת המצולע המשוכלל בן 65,537 צלעות. לעומת זאת, לא ניתן לבנות את המצולע המשוכלל בן 9 צלעות (משום שזה יצריך בניית זווית של 20 מעלות, בנייה שאינה אפשרית בסרגל ומחוגה).
בניית מספרים[עריכת קוד מקור | עריכה]
אם נתון קטע היחידה, כלומר קטע שאורכו 1, אז ניתן להגדיר "מספר חיובי הניתן לבנייה". כיוון שאפשר לחבר קטעים, אפשר לקבל כל מספר טבעי. ניתן גם לבצע פעולות נוספות:
כדי לכפול קטעים u ו-v, יש לבנות את הקטע OA שאורכו 1, ו-AC שאורכו u באופן ששלוש הנקודות על אותו ישר. אחר כך בונים OB שאורכו v כך ש-B לא על אותו ישר. בונים מ-C ישר מקביל ל-AB וקוראים לנקודת החיתוך שלהם D. על פי משפט תאלס מתקיים:
- , כלומר ומכאן BD=uv כמבוקש.
כדי לחלק קטעים יש למצוא מספר הופכי, כלומר אם נתון u יש למצוא את . ניתן לעשות זאת באותה דרך, כאשר הפעם בונים כך ש-OA=u, AC=1 ו-OB=1 ואז: ומכאן BD=1\u כמבוקש. מה שהוסבר עד כה מספיק כדי לבנות כל מספר רציונלי חיובי.
פעולה נוספת שניתן לעשות היא הוצאת שורש ריבועי. כדי לעשות זאת יש לבנות קטע AB באורך a (ממנו רוצים להוציא שורש) וקטע BC שאורכו 1 כך ששני הקטעים על אותו ישר. לאחר מכן לבנות מעגל שקוטרו AC, ואז לבנות אנך ל-AC מהנקודה B ולקרוא לנקודת החיתוך שלו עם המעגל D. מתקיים , ולכן על פי תכונות דמיון משולשים מתקיים או ומכאן כמבוקש.
מספרים מרוכבים[עריכת קוד מקור | עריכה]
לאחר שנתונות זוג נקודות, להן אפשר להתייחס כנקודות 0 ו- 1, מגדירים מספר מרוכב כנקודה שהוא מציין על המישור המרוכב. קבוצת המספרים הניתנים לבנייה בצורה כזאת מהווים שדה הנקרא שדה המספרים הניתנים לבנייה. ניתן לבנות מספר a+bi אם ורק אם ניתן לבנות את |a| ואת |b|, אותם בונים כמוסבר לעיל.
למספרים הניתנים לבנייה תכונות נוספות. כך למשל, מספר ניתן לבנייה אם ורק אם הוא שייך לשדה הנמצא בקצה של מגדל הרחבות ריבועיות (הרחבות מממד 2) של שדה המספרים הרציונליים.
הכללות[עריכת קוד מקור | עריכה]
אף על פי שבבעיות הבנייה הקלאסיות מקובל היה להשתמש בשני הכלים, הסרגל והמחוגה, ידוע שאפשר להסתפק בהרבה פחות. בשנת 1797 פרסם הגאומטרן האיטלקי לורנצו מסקרוני ספר, שבו הראה שכל בעיה שאפשר לבנות בסרגל ומחוגה, אפשר לבנות גם באמצעות המחוגה לבדה[1]. כדי להראות זאת, הוכיח מסקרוני שבמחוגה ניתן לחבר ולחסר ארכי קטעים, וגם להכפיל ולחלק אורכים זה בזה. (לא ניתן לבנות ישרים, אך ניתן למצוא שתי נקודות המתוות את הישר, ולמעשה לשרטט נקודות כרצוננו הנמצאות על הישר).
כבר ב-1759 עסק ד'אלמבר בפתרון בעיות בנייה בסרגל בלבד. בעיות אלה מטבען מוגבלות יותר מאשר הבניות במחוגה ובסרגל, משום שהסרגל אינו מאפשר אלא פתרון של משוואות ליניאריות. עבודתו של ד'אלמבר המריצה מתמטיקאים צרפתיים אחרים לעסוק בנושא, שהעניין בו גבר אחרי פרסום ספרו של מסקרוני. באותה עת הציע ז'אן-ויקטור פונסלה (Jean-Victor Poncelet; 1867-1788) שהוספת מעגל אחד קבוע במישור (יחד עם המרכז של אותו מעגל), די בה כדי לאפשר לסרגל לפתור כל בעיית בנייה במחוגה וסרגל. השערה זו הוכחה ב-1833 על ידי הגאומטרן יאקוב שטיינר, וזכתה לשם משפט פונסלה-שטיינר.
כלי נוסף שניתן להגדיר הוא "סרגל דו-צדדי" ― כלי שבהינתן ישר, מסוגל לבנות ישר מקביל במרחק קבוע (רוחב הסרגל), ובהינתן שתי נקודות שמרחקן גדול מרוחב הסרגל, מסוגל לבנות ישר דרך אחת מהן שמרחקו מהשנייה שווה לרוחב הסרגל. כל בעיה שאפשר לבנות בסרגל ומחוגה, אפשר לבנות באמצעות סרגל דו-צדדי בלבד.[2]
היפיאס הראה שבעזרת קוואדרטריקס, כלי שאיננו בארגז הכלים של הגאומטריה, ניתן לחלק זווית נתונה לשלושה חלקים, וכן הוכח שכלי זה מאפשר את תרבוע העיגול.
כלי אחר שנעשה בו שימוש בהקשר דומה, הוא "הסרגל המסומן" או ה-neusis construction (אנ'), כלי שבהינתן קטע, נקודה, ושני קווים, בונה נקודה על כל אחד מהקווים כך ששלוש הנקודות ― הנתונה ושתי החדשות ― נמצאות על ישר אחד, והמרחק בין שתי החדשות הוא כאורך הקטע הנתון. כלי זה ניתן ל"מימוש" על ידי סרגל, עליו ניתן לסמן אורך של קטע נתון, ואז להניח אותו על הנקודה הנתונה, ולאפשר לו להסתובב ולהחליק על גביה, עד ששני קצות הקטע שמסומן עליו ייגעו בשני הקווים הנתונים ― ואז לבנות את הקו שהוא מתווה.
ה-neusis construction מספק פתרון נאה לכמה מהבעיות שהוזכרו קודם לכן, כמו הבעיה של הכפלת הקובייה (אותה אפשר לפתור גם באמצעות חיתוך של פרבולות, או בעזרת העקום הקרוי קונכואיד, שבנייתו מיוחסת לניקומדס, בן המאה השנייה לפני הספירה). ארכימדס הראה שאפשר, בעזרת סרגל, מחוגה ו-neusis construction, לחלק זווית נתונה לשלושה חלקים.
ניתן להגדיר עקום שלישי זווית (אנ'), ואז בעזרת סרגל ומחוגה לחלק זוויות ל-3 חלקים שווים.
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Heinrich Dorrie, 100 Great Problems of Elementary Mathematics, (translated 1965).
- בניות גאומטריות - בעיות קלאסיות, אתגריות וממוחשבות, הוצאת שאנן. 2015.
- חידושים בגיאומטריה אוקלידית - תיאוריה של מרובע קמור ומעגל היוצר נקודות פסקל על צלעותיו, הוצאת אקדמון, 2021.
- בעיות בנייה חדשות ומתאימות לתלמידי תיכון, כנס ירושלים ה12 למחקר בחינוך מתמטי, עמ' 139-142.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- כלים לבנייה וירטואלית בסרגל ומחוגה
- גדי אלכסנדרוביץ', בניות בסרגל ומחוגה – המשחק!, באתר "לא מדויק", 23 ביוני 2014
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ בנייה באמצעות מחוגה בלבד
- ^ סנדרה קיי בירל, עבודת גמר לתואר מוסמך במכון הטכנולוגי של קליפורניה, מאי 1983. העבודה עוסקת בכלים נוספים; הפרק שנוגע לסרגל הדו צדדי מתחיל בעמוד 50.










