גאומטריה ספירית

גאומטריה ספֵירִית היא סוג של גאומטריה לא אוקלידית, העוסקת בתכונות של ישרים על ספירה, דהיינו מעטפת של כדור. כאשר רדיוס הכדור שואף לאינסוף מתקבלת הגאומטריה המישורית, האוקלידית.

בגאומטריה הספירית הקווים הישרים הם "מעגלים גדולים" - כאלה שרדיוסם שווה לרדיוס הכדור (אלו הם הקווים הגאודזיים במטריקה הסטנדרטית של הספירה). משום כך, כל שני ישרים נחתכים, והגאומטריה אינה אוקלידית. היחס "בין", המשחק תפקיד מרכזי באקסיומטיקה של הילברט לגאומטריה האוקלידית, אינו קיים בגאומטריה הספירית.

השוואה לגאומטריה האוקלידית[עריכת קוד מקור | עריכה]

גאומטריה אוקלידית	גאומטריה ספירית
אקסיומת המקבילים: דרך כל נקודה עובר ישר אחד ויחיד המקביל לישר נתון.	כל שני ישרים נחתכים.
סכום הזוויות במשולש שווה ל 180⁰	סכום הזוויות במשולש גדול מ 180⁰
קיימים מלבנים.	לא קיימים מלבנים.
קיימים משולשים דומים שאינם חופפים	שני משולשים השווים בשלוש זוויותיהם הם חופפים.
לכל שלוש נקודות על אותו ישר, בדיוק אחת מהן נמצאת בין שתי האחרות.	היחס "בין" לא קיים.

שטח מצולע[עריכת קוד מקור | עריכה]

כאמור, במשולש ספירי מתקיים: $\ \alpha +\beta +\gamma >180^{\circ }$ וברדיאנים: $\ \alpha +\beta +\gamma >\pi$ . ההפרש $\ E=\alpha +\beta +\gamma -\pi$ נקרא מגרעת המשולש. שטח המשולש נתון על ידי הנוסחה: $\ E\cdot R^{2}$ .

באופן כללי, אם נסמן את המגרעת של מצולע בעל n צלעות: $\ E=\alpha _{1}+...+\alpha _{n}-(n-2)\pi$ כאשר $\ \alpha _{1},...,\alpha _{n}$ הן זוויות המצולע, אזי שטח המצולע שווה ל $E\cdot R^{2}$ .

טריגונומטריה ספירית[עריכת קוד מקור | עריכה]

ערך מורחב – טריגונומטריה ספירית

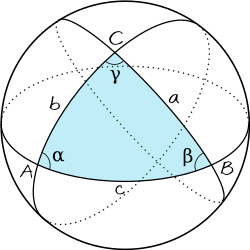
המשפטים המוכרים מהגאומטריה ומהטריגונומטריה האוקלידית, אינם מתקיימים בגאומטריה הספירית, אך קיימים להם משפטים מקבילים בטריגונומטריה זו:

משפט פיתגורס - $\cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\,\cos \left({\frac {b}{R}}\right)$ .
משפט הקוסינוסים - $\,\cos {\frac {c}{R}}=\cos {\frac {a}{R}}\cdot \cos {\frac {b}{R}}+\sin {\frac {a}{R}}\cdot \sin {\frac {b}{R}}\cdot \cos \gamma$ .
משפט הסינוסים - ${\frac {\sin {\tfrac {a}{R}}}{\sin \alpha }}={\frac {\sin {\tfrac {b}{R}}}{\sin \beta }}={\frac {\sin {\tfrac {c}{R}}}{\sin \gamma }}$ .