קוואזי-גביש
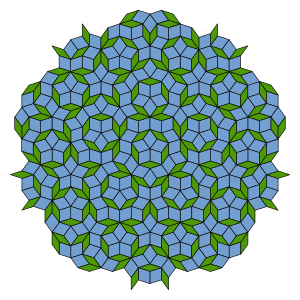
קוואזי-גביש, גביש כמו-מחזורי,[1] גביש קווזיפריודי הוא גביש שבניגוד לגבישים רגילים, שהם בעלי סריג מחזורי, הוא בעל סימטריה שאיננה מסתדרת עם מחזוריות. סימטריה משולשת, מרובעת או משוּשָה מאפשרת מחזוריות במישור, ואילו לגבישים כמו-מחזוריים ישנה סימטריה שאינה מתיישבת עם מחזוריות במישור (כמו למשל סימטריה מחומשת או מתומנת), וניתן להסבירה על ידי הדוגמה של ריצוף פנרוז. היא יוצרת כמו-מחזוריות במישור אך מחזוריות במישור הניצב לו. גבישים אלו התגלו לראשונה על ידי פרופסור דן שכטמן מהטכניון ב-1982, באמצעות התאבכות של קרני רנטגן בסריג גבישי ויצירת תבנית פיזור בראג. על תגלית זו זכה שכטמן בפרס נובל לכימיה לשנת 2011.
גילוי וחקר גבישים כמו-מחזוריים[עריכת קוד מקור | עריכה]
בשנת 1984 התחוללה מהפכה זוטא בתחום הפיזיקה של חומר מעובה. דן שכטמן מהטכניון פרסם את תגליתו – קיום גביש בעל סימטריה איקוֹסהדרית (של עשרימון), הכוללת סימטריה גבישית מחומשת. שכטמן גילה אותו כבר באפריל 1982, אך הממצא נחשב אז לחריג ביותר ופרסומו התעכב למעלה משנתיים בגלל חוסר האמון של הממסד המדעי. עד אז סדר גבישי נחשב לנרדף לסדר מחזורי (ראו סריגי בראבה). חודש אחד אחרי פרסומו של שכטמן ושותפיו, פרסמו לוין ושטיינהארדט (Levin, Steinhardt) הסבר לתופעה, לפיה אפשר היה להבין את הגבישים החדשים באמצעות הריצוף הקווזיפריודי של רוג'ר פנרוז.
לא ניתן לרצף את המישור במחומשים משוכללים, ועובדה זו הייתה ידועה מזמן. בשנות השבעים של המאה העשרים מצא האסטרופיזיקאי פנרוז, ריצוף בעל סימטריה מחומשת שאינו מחזורי, אלא כמו-מחזורי בלבד. ריצוף זה מבוסס על שתי מרצפות מעוינות, הנגזרות ממחומש משוכלל. ליישום במדעי הטבע מעדיפים לרוב את גרסת שתי המרצפות המעוינות.
לאחר תגליתו של שכטמן והופעת כמה הצעות להסבר תאורטי לתופעה, נפתחה הדלת לגילויים חדשים. נמצאו גבישים נוספים שקיומם נחשב לבלתי אפשרי. אישימאסה ושותפיו (Ishimasa) מצאו גבישים בעלי סימטריה דוֹדֶקאגוֹנאלית (מתורסרת). בנדרסקי (Bendersky) מצא גבישים פּנטגוֹנאליים/דֶקאגוֹנאליים, דהיינו בעלי סימטריה מחומשת, שהיא בעצם מעושרת. כעבור כשנה מצאו ואנג ושותפיו מקבוצת פרופסור קוּאוֹ בבייג'ינג (Wang) גבישים אוֹקטאגוֹנאליים (מתומנים). אחרי גילויים אלה התפשט והתעמק חקר הגבישים הקווזיפריודיים, והתגלו מאות סוגים של גבישים חדשים.
באפריל 2006, חוקרים מהפקולטה לפיזיקה בטכניון, בהנחיית פרופסור מוטי שגב, יצרו גביש כמו-מחזורי פוטוני, המגיב בצורה דינמית לאור העובר דרכו. הם הכניסו פגם באופן מכוון לגביש, והראו, בזמן אמת, כיצד הגביש מתקן את עצמו באמצעות אינטראקציה דינמית עם האור. תופעה ייחודית זו נוטעת תקווה שפיתוחים עתידיים בתחום יוכלו לרתום את התכונות החדשות ליצירת טכנולוגיות ושימושים נוספים לגבישים מסוג זה.
ההבדל בין גביש קלאסי לגביש קווזיפריודי[עריכת קוד מקור | עריכה]
הגביש הקלאסי[עריכת קוד מקור | עריכה]
 ערך מורחב – קריסטלוגרפיה
ערך מורחב – קריסטלוגרפיה
במשך מאות שנים נחשב גביש לגוף מוצק, אשר צורתו החיצונית דומה לפאון. דוגמאות מובהקות היו אבנים טובות כמו יהלום ואמטיסט מחד, ומאידך גבישי מלח בישול וסוכר. קפלר ואַאִי שיערו שהצורה החיצונית היא תולדה של המבנה הפנימי, אשר הוא מערך מסודר של יחידות בסיס זהות. בתחילת המאה העשרים הוכיחו את ההשערה הזאת פֿרידריך, קניפּינג ופֿוֹן לַאוּה על ידי הניסויים הראשונים של קריסטלוגרפיה בקרני רנטגן. מאז הוסכם כי גביש הוא מערך מחזורי של אטומים. ההגדרה הפורמלית של מבנה גבישי מחזורי מתבססת על סריג בראבה והיא כדלקמן:
- סריג n-ממדי הוא קבוצת הנקודות באשר הם וקטורים בלתי-תלויים ליניארית.
- המקבילון הפרוס על הווקטורים נקרא תא יחידה. מתמטיקאים מעדיפים לכנותו "תחום יסודי". מן ההגדרה ברור שתא היחידה נשנה מחזורית במרחב כולו.
- מוטיב (לעיתים נקרא גם "בסיס") הוא דוגמה הממלאת את תא היחידה. בטבע זהו מערך האטומים.
- מבנה גבישי הוא צירוף של סריג בראבה ומוטיב. התוצאה היא מערך אטומים מחזורי (ולכן אינסופי).

הגביש הקווזיפריודי[עריכת קוד מקור | עריכה]
הגביש הקווזיפריודי בממד אחד[עריכת קוד מקור | עריכה]
המודל הראשון לגביש קווזיפריודי נזקף לזכות פיבונאצ'י, אף שהוא לא ידע כי הוא מפתח מודל. בספרו ספר החשבונייה (Liber abbaci) שפרסם בשנת 1202, שאל פיבונאצ'י את השאלה הבאה: "כמה זוגות ארנבות יהיו בחלוף שנה, אם בתחילתה ישנו זוג בודד של ארנבות בוגרות, ובחלוף כל חודש נולד לכל זוג בוגר זוג ארנבות צעיר, אשר מתבגר כעבור חודש?". אם נסמן זוג ארנבות בוגר באות L וזוג צעיר באות S, נוכל ליצור את סדרת האותיות המופיעות בטבלה שלהלן וכך לענות על שאלתו של פיבונאצ'י. נקודת ההתחלה היא זוג ארנבות בוגר L, ועבור כל חודש שעובר תוחלף כל הופעה של האות L ברצף האותיות LS, וכל הופעה של האות S באות L. נבצע אפוא את ההצבה:
S→L
L→LS
מספר הארנבות בכל חודש שווה למספר הארנבות שהיו חודש קודם לכן, ועוד מספר הארנבות שנוספו. בצורה כזאת תתקבל סדרת פיבונאצ'י הידועה: ...,13 ,8 ,5, 3 ,2 ,1, 1.
אם נמשיך בתהליך החלפת האותיות הזה אינסוף פעמים, תתקבל שרשרת אינסופית של שתי האותיות L ו-S בעלת סדר ארוך-טווח, העונה על הגדרת הקווזיפריודיות שצוינה לעיל. נחוץ להדגיש שסדרת האותיות איננה מחזורית – לא ניתן להסיט אותה במספר סופי של אותיות לימין או לשמאל, כך שהיא תתלכד עם עצמה. עם זאת, ישנם קטעים רבים של אותיות, בעלי אורך סופי, שחוזרים על עצמם במקומות שונים לאורך השרשרת. השרשרת היא מסודרת אך איננה מחזורית.
כדי לקבל מודל לגביש קווזיפריודי חד-ממדי, עלינו להניח אטומים לאורך ישר אינסופי כאשר המרחקים ביניהם נקבעים על פי סדרת האותיות: מרחק ארוך (מסומן ב-L) או קצר (S), לפי הכללים שתוארו. אפשר לבנות בפועל חומר כזה באמצעות אפיטקסיה בקרן מולקולרית (Molecular beam epitaxy), שהיא הנחת שכבה גבישית דקה על גביש אחר. באופן זה יוצרים שכבות עוקבות של שני סוגי אטומים. אם נבצע בדיקה קריסטלוגרפית על הגביש שיצרנו, נקבל שיאי בראג מושלמים, המעידים על קיומו של סדר ארוך-טווח. מספר וקטורי הבסיס הנחוץ כדי לאפיין את השיאים בעלי אינדקסים שלמים הוא שניים, כלומר גדול ממספר הממדים שהוא אחד. זה אופייני לקווזיפריודיות, וזאת להבדיל ממבנה מחזורי, אשר מספר וקטורי הבסיס שלו שווה לממד.
גביש קווזיפריודי במישור[עריכת קוד מקור | עריכה]
עם גילוי גבישים בעלי סימטריה מחומשת, נוצר המושג גביש קווזיפריודי. גביש בעל סימטריה מחומשת אינו יכול להסתדר בצורה מחזורית במישור, מכיוון שלא ניתן לסדר מחומשים משוכללים במישור מבלי שייווצרו חפיפות או פערים. גילוי זה הוסבר במאמר של לוין ושטיינהארדט (Levine, Steinhardt). לדבריהם יכולה להתקיים סימטריה מחומשת במישור, על ידי שימוש בריצוף פנרוז.
קיומם של גבישים מסוג זה סותר את ההגדרה הקלאסית של הגביש, מכיוון שגבישים אלה אינם מחזוריים. אי לכך היה צורך להגדיר מחדש את מושג הגביש. כיום אין עדיין הסכמה מוחלטת על הגדרת המושג "גביש", אך לפי ההגדרה הרשמית התקפה, גביש הוא מוצק אשר תמונת דיפרקציית קרני ה-X שלו היא בעיקרה בדידה, כלומר שניתן לקבל נקודות בראג בדיפרקציית קרני רנטגן.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- רון ליפשיץ, קווזי-גבישים: מקפלר ועד שכטמן, פיזיקהפלוס, גיליון 3, 2004
- ריצוף פנרוז וריצופים קווזי-מחזוריים: באתר זה ניתן למצוא מידע נוסף על ריצוף פנרוז שהמציא הפיזיקאי רוג'ר פנרוז, שהוא הכרחי להבנת הגבישים הכמו-מחזוריים.
 דן שכטמן, הגדרה חדשה מהו גביש, הרצאה בסדרת ההרצאות "בכור המהפכה", 23 באפריל 2012
דן שכטמן, הגדרה חדשה מהו גביש, הרצאה בסדרת ההרצאות "בכור המהפכה", 23 באפריל 2012- קוואזי-גביש, באתר אנציקלופדיה בריטניקה (באנגלית)
- ^ גדי אלכסנדרוביץ', גבישים כמו-מחזוריים וריצופים כן-מחזוריים, באתר "לא מדויק", 10 באוקטובר 2011
