זרימה טורבולנטית
יש לערוך ערך זה. הסיבה היא: הסברים בגוף הערך לא נהירים ואינם מספקים, המשוואות אינן מוסברות דיין אף לא לקורא בעל רקע מדעי.
| ||
| יש לערוך ערך זה. הסיבה היא: הסברים בגוף הערך לא נהירים ואינם מספקים, המשוואות אינן מוסברות דיין אף לא לקורא בעל רקע מדעי. | |
במכניקת הזורמים, זרימה טורבולנטית (זרימה עירבולית) היא זרימת נוזל באופן לא מסודר ואקראי. על כן ניתן לחשב את התנהגותה הממוצעת לאורך הזרימה בלבד, וקשה להסיק על נתוני הזרימה בנקודה כלשהי לפי נקודה סמוכה. רוב הזרימות הטבעיות והתעשייתיות, כגון זרימה באטמוספירה, באוקיינוסים, במכוניות ובמטוסים, הן טורבולנטיות בשלמותן או במקצתן. בזרימה טורבולנטית ניתן לראות כי פרמטרים מרכזיים של הזרימה, כגון מהירות ולחץ משתנים בצורה אקראית, כתוצאה מכך יש לזרימה מגוון רחב של זמנים ומרחקים אופייניים.[1]

זרימה טורבולנטית מאופיינת בשלוש תכונות מרכזיות:
זרימה "מסודרת", שאינה טורבולנטית, נקראת זרימה למינרית.
זרימה טורבולנטית נגרמת על ידי עודפים של אנרגיה קינטית בחלקים של הזרימה, אשר גוברים על האפקט המרסן של צמיגות הזורם. מסיבה זו קל יותר לייצר טורבולנציה בזורמים בעלי צמיגות נמוכה מאשר בזורמים בעלי צמיגות גבוהה במיוחד. במילים אחרות, החל ממהירות מסוימת, מערכת הזרימה הופכת רגישה במיוחד להפרעות זעירות בזרימה (כמו בכל מערכת כאוטית), והטורבולנציה צומחת באופן מורכב מתוך הבדלים קטנים במהירות וכיוון הזרימה המקומי, זאת שכן הצמיגות האופיינית שלה אינה מסוגלת לרסן את ההפרעות הקטנות ולהחזיק את המערכת במצב היציב של זרימה למינרית סדורה.
כדי לנבא אם תתפתח בזרימה מסוימת זרימה למינרית או טורבולנטית, מקובל להסתכל על מספר ריינולדס. מספר ריינולדס מראה האם הזרימה תגביר הפרעות (במספרי ריינולדס גבוהים) ואז תיווצר זרימה טורבולנטית. כך, בזרימה בצינור מקובל להגיד שיש מעבר לזרימה טורבולנטית במספר ריינולדס של כ-2000. עם זאת, ניתן לדחות התפתחות טורבולנציה על ידי הפחתת ההפרעות (לדוגמה על ידי שינוי צורת הכניסה של הזורם למערכת).
חתן פרס נובל ריצ'רד פיינמן תיאר זרימה טורבולנטית בתור "הבעיה הלא פתורה החשובה ביותר של הפיזיקה הקלאסית."[2] כמו כן, לפי אגדה אורבנית, כאשר ורנר הייזנברג נשאל מה הוא היה שואל את אלוהים לו ניתנה לו ההזדמנות, הוא ענה: "כאשר אפגוש את אלוהים, אשאל אותו שתי שאלות: למה יחסות? ולמה טורבולנציה? ואני באמת חושב שתהיה לו תשובה לראשון."[3]
ערכים ממוצעים[עריכת קוד מקור | עריכה]

עקב האי-סדר בזרימה טורבולנטית, מקובל להסתכל במקרים רבים על הערכים הממוצעים של המהירות.
כך למשל, אם נגדיר את כרכיב המהירות הרגעית בכיוון מסוים, נקבל שהמהירות הממוצעת מקיימת את המשוואה: . הערך הרגעי מורכב משני רכיבים, ערך ממוצע וערך תונד: . כאשר ממוצע התנודות מתאפס . ניתן למדוד את עוצמת הטורבולנטיות בעזרת שורש ממוצע הריבועים של המהירות: [1] ניתן לעשות ניתוח דומה עבור מהירות ומהירות בכיוונים הניצבים.
משוואת ריינולדס הממוצעות[עריכת קוד מקור | עריכה]
אם ניקח זמן מספיק גדול כך שיכיל הרבה מערבולות אך קטן מהזמן האופייני של המערכת, נוכל לפתח את משוואת הרציפות הממוצעת:
ומכך נובע עבור החלק התונד: .
וממשוואות נאוויה-סטוקס בכיוון נקבל את הקשר:
כאשר האיבר נקרא איבר מאמצי ריינולדס.
באופן כללי נקבל מטריצת מאמצי ריינולדס:
בסך הכל יש לנו 4 משוואות (3 משוואות נאוויה-סטוקס ומשוואת הרציפות) עם 6 נעלמים, לכן מקובל לפתור את משוואות אלו בעזרת הנחות שונות, בהתאם למקרה הנחקר.
השפעת מספר ריינולדס[עריכת קוד מקור | עריכה]
מעבר למספר ריינולדס מסוים, זרימה למינרית נהיית לא יציבה. הערך של מספר ריינולדס בו מעבר זה קורה תלוי בתדירות ההפרעה, הערך ההתחלי של ההפרעה, סוג גרדיאנט הלחץ, צורת וחספוס שכבת הגבול וכו'.[1]
כאשר הזרימה טורבולנטית, קשה להבדיל בסקאלת המאקרו בין זרימה עם מספרי ריינולדס אחד למספר ריינולדס אחר (בתנאי שהזרימות כולן טורבולנטיות והגאומטריה דומה). עם זאת, בסקאלת המיקרו, ניתן לראות כי המערבולות יותר קטנות ככל שמספר ריינולדס גדל. תופעה זו נובעת מכך שאפילו במספרי ריינולדס גבוהים (בהן כוחות הצמיגות קטנות יחסית לכוחות האינרציה), כוחות הצמיגות גורמות למערבולות הגדולות להתפצל למערבולות קטנות יותר עד שמגיעים לגדלים שבהן הצמיגות שולטת.
מערבולות[עריכת קוד מקור | עריכה]
היווצרותן של מערבולות גדולות נוצרת בעקבות תנודתיות אקראית של התנועה הטורבולנטית בסקאלת המיקרו שמוגברת בנוכחות גרדיאנטי מהירות ממוצעת. המערבולות הגדולות הללו נוצרות מאי-יציבות פרופילי המהירות הממוצעת להפרעות בקנה מידה קטן של הזרימה הטורבולנטית. המערבולות הגדולות סופגות את האנרגיה של הזרימה הממוצעת. הן אחראיות בעיקרן על תהליכי דיפוזיה וערבוב ומעבירות טורבולנציה, תנע, ערבוליות, חום, חומר וחלקיקים בדידים. מערבולות גדולות אינן בעלות תכונות קבועות, אלא הן מתארכות ונמתחות בעקבות אינטראקציה אינרציאלית עם מערבולות שכנות. כאשר הן נמתחות ומתפתלות, ישנה היווצרות של צווארים צרים והן מתפצלות למערבולות קטנות. למערבולות הקטנות אנרגיה טורבולנטית ועוצמה ערבולית גבוהה יותר. כך, יש מעבר אנרגיה מהמערבולות הגדולות לקטנות. עם זאת, ישנו גבול שבו מערבולות עוד יותר קטנות כבר אינן יותר אנרגטיות מהמערבולות מהן נוצרו. כאשר המערבולות נהיות קטנות בהדרגתיות, גרדיאנט המהירות לאורך המערבולת מביא לדיסיפציה של אנרגיה טורבולנטית לחום בעזרת הצמיגות.[1]
מודל אורך הערבוב של פרנטל[עריכת קוד מקור | עריכה]
התאוריה של לודוויג פרנטל (אנ') מציגה ביטויים ל ול בעזרת אורך ערבוב וגרדיאנט מהירות כאשר זה המרחק הנורמלי ל- שנמדד לרוב מהשפה. פרנטל הניח, שבדומה לגז, בו מולקולה אחת עוברת מהלך חופשי ממוצע לפני שמתנגשת בשנייה - כך גם חלקיק בזורם עובר מרחק לפני שהתנע שלו משתנה בסביבה החדשה. בעזרת שימוש במשוואה הזו ובמשוואת הרציפות, הוא קיבל כי הקשר בין התנודתיות ו לאורך הוא: .
כלומר, השינוי במהירות תלוי בשינויים בממוצע בזמן של המהירות בשתי נקודות במרחק אחד מהשני בכיוון .
המשוואה השולטת לאורך הערבוב שהוא קיבל היא:
כאשר גורם לפילוג המהירות להפוך ליותר אחיד.
היחס בין למרחק לקיר לא ניתן בפיתוח של פרנטל. תיאודור פון קרמן הציע את הקשר: כאשר הוא קבוע אוניברסלי לזרימה טורבולנטית, שאינו תלוי בתנאי השפה או במספר ריינולדס.[4]
שכבת גבול טורבולנטית[עריכת קוד מקור | עריכה]
משוואות ריינולדס הממוצעות לשכבת גבול טורבולנטית[עריכת קוד מקור | עריכה]
למקרה דו-ממדי, בלתי דחיס ותמידי:
לא קיים פתרון מדויק למשוואות אלו, אך בעזרת אנליזה ממדית ניתן לפשט את הבעיה ולמצוא דמיון בין מקרים שונים. האנליזה הממדית מבוססת על הגדרת מהירות חיכוך , מהירות מנורמלת , ומרחק מנורמל .
המודל הלוגריתמי של פון קרמן[עריכת קוד מקור | עריכה]
תיאודור פון קרמן הציע מודל: כאשר הקבועים נקבעים על ידי ניסויים ונכונים עבור גאומטריות ומספרי ריינולדס קרובים לאלו שהיו בניסוי. בצינורות חלקים, קרוב לגבול, הקבוע (קבוע פון קרמן) הוא בקירוב 0.4, והערך הוא 5.5.[1] ובצורה ממדית המשוואה היא מהצורה:
שכבות בשכבת הגבול[עריכת קוד מקור | עריכה]
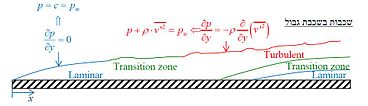
באזור הטורבולנטי של שכבת הגבול, ישנה חלוקה לתתי שכבות - אזור טורבולנטי, אזור מעבר ואזור למינרי. זאת, כיוון שממש צמוד לקיר נקבל מהירויות אפסיות ובהגדלה מספיק משמעותית, כל ערבול מורכב מקווי זרם למינריים. עבור לוח שטוח מעבר לשכבת גבול טורבולנטית מתרחשת במספרי ריינולדס של . תת-שכבת הגבול הלמינרית מוגבלת לאזור . בתוך תת-שכבת הגבול הלמינרית, הצמיגות היא האיבר המשמעותי ביותר המכתיב את הזרימה ולכן משוואת נאוויה סטוקס המתקבלת באזור זה היא: אזור המעבר מוגדר לפי: שכבת הגבול הטורבולנטית מוגדרת כאשר:
קירוב חזקות[עריכת קוד מקור | עריכה]
עבור לוח שטוח שמבחוץ זורם זרם בזווית אפס מעלות ביחס ללוח, מתקבל הקשר:
כאשר - מאמץ הגזירה, - עובי תנע שהלך לשכבת הגבול, ו- - המהירות רחוק מהלוח.
עבור לוח חלק, פול בלסיוס (אנ') פיתוח נוסחה אמפירית למאמץ הגזירה:
כמו כן, חוק פילוג החזקות של פרנטל אומר:
ולכן נקבל את הקשרים הבאים לעובי ההזזה, תנע, ואנרגיה בהתאמה:
כאשר הערך של תלוי במספר ריינולדס.[1]
צינורות[עריכת קוד מקור | עריכה]
עבור ניתוח של זרימה בצנרת מקובל להשתמש בדיאגרמת מודי המאפשר מציאת מקדם החיכוך של זרימה בצינור כתלות במספר ריינולדס ובחספוס של הצינור. הדיאגרמה מראה מספר תחומים בזרימה בצינור והם:
- זרימה למינרית, בה מתקיים כאשר הוא מקדם החיכוך ו- הוא מספר ריינולדס;
- אזור קריטי בו הזרימה אינה מוגדרת;
- אזור מעבר בו מקדם החיכוך מוגדר על ידי החיספוס היחסי ומספר ריינולדס;
- אזור הזרימה הטורבולנטית המלאה בו נראה מקדם החיכוך כקו אופקי לפי החספוס היחסי של דופן הצינור.
לקריאה נוספת[עריכת קוד מקור | עריכה]
- ד"ר רמי אורון, זרימה טורבולנטית על פני משטחים חלקים, 2020 (באנגלית)
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- זרימה טורבולנטית, באתר אנציקלופדיה בריטניקה (באנגלית)
 מערבולת, דף שער בספרייה הלאומית
מערבולת, דף שער בספרייה הלאומית
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ 1 2 3 4 5 6 Narasimhan, S. A first course in fluid mechanics. Hyderabad, India Boca Raton: Universities Press CRC Press, 2007
- ^ "Turbulence theory gets a bit choppy". USA Today. September 10, 2006. (הקישור אינו פעיל, 5.1.2024)
- ^ MARSHAK, ALEX (2005). 3D radiative transfer in cloudy atmospheres; pg.76. Springer. ISBN 978-3-540-23958-1.
- ^ Streeter, Victor (1998). Fluid mechanics. Boston: WCB/McGraw Hill. ISBN 0070625379.






![{\displaystyle {\sqrt {\overline {u{{'}^{2}}}}}={{\left[{\underset {T\to \infty }{\mathop {\lim } }}\,\int _{0}^{T}{u{{'}^{2}}dt}\right]}^{\scriptstyle {}^{1}\!\!\diagup \!\!{}_{2}\;}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a34e3465ae6e2adc63a6f66cfb329d34fff410a6)












































