טנזור מאמצים

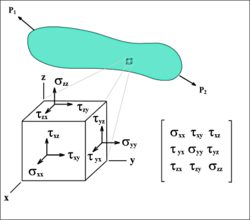
טנזור המאמצים

טנזור המאמצים בתיאור אינדקסים כללי

טנזור המאמצים הוא מטריצה בת תשעה רכיבים ( 3 על 3) המתאר את המאמצים על פני קובייה קטנה של החומר הנתון בעומס חיצוני. טנזור המאמצים מרכז את מאמצי המתיחה, הלחיצה והגזירה, הפועלים על הגוף.

טנזור המאמצים

$T = \left( \begin{matrix} \sigma_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \\ \end{matrix} \right)$

משווי משקל מקבלים מטריצה סימטרית ובה 6 רכיבים שונים. מתקיים השוויון בין הרכיבים:

• $\ \tau_{xy}=\tau_{yx}$
• $\ \tau_{zx}=\tau_{xz}$
• $\ \tau_{zy}=\tau_{yz}$

לכן:

$T = \left( \begin{matrix} \sigma_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{xy} & \sigma_{yy} & \tau_{yz} \\ \tau_{xz} & \tau_{yz} & \sigma_{zz} \\ \end{matrix} \right)$

טנזור המאמצים הוא טנזור סימטרי ותמיד אפשר להציג אותו כסכום של שני טנזורים סימטריים שהם:

• טנזור ממוצע או מאמצים הידרוסטטי הכולל מאמצי מתיחה או לחיצה בלבד
• טנזור מאמצי גזירה הכולל מאמצי גזירה בלבד.

תיאור כללי

התיאור הכללי של טנזור המאמצים נעשה באמצעות אינדקסים 1,2,3

x	→	1
y	→	2
z	→	3
σxx	→	σ11
τxy	→	σ12
τxz	→	σ13
...

ונקבל:

$T = \left( \begin{matrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \\ \end{matrix} \right)$

את חוק הוק אפשר להציג באמצעות המינוח הזה של האינדקסים בצורה הבאה:

$\sigma_{ij} = \sum_{kl} C_{ijkl} \cdot \varepsilon_{kl}$

תורת היחסות

טנזור מאמץ-אנרגיה יחסותי ורכיביו

בתורת היחסות טנזור המאמצים הוא חלק מטנזור 4 על 4 הנקרא טנזור צפיפות האנרגיה או טנזור המאמץ-אנרגיה ומסומן $\ T_{\mu \nu}$ (כאשר $\ \mu,\nu = ct, x, y, z = 0,1,2,3$): זהו טנזור סימטרי שכולל את צפיפות האנרגיה, שטף האנרגיה, תנע ואת טנזור מאמצים (תת-מערך בגודל 3 על 3). טנזור זה מופיע במשוואת השדה של איינשטיין $\ G_{\mu \nu} = \frac{8 \pi G}{c^4} T_{\mu \nu}$ (כאשר $\ G_{\mu \nu}$ הוא טנזור איינשטיין) המתארת את עקמומיות המרחב-זמן כתלות בהתפלגות צפיפות האנרגיה, המסה, התנע והלחץ במרחב-זמן.

ראו גם

• מאמץ (הנדסה)

קישורים חיצוניים

• מאמצים וטנזור מאמצים, באנגלית
• טנזור מאמצים וטנזור מעוותים, באנגלית
• טנזור המאמצים, באנגלית

לקריאה נוספת

• Timoshenko S.P, Strength of Materials, 3rd edition, Krieger Publishing Company, 1976. ISBN 0882754203
• S.P. Timoshenkoo & J.N. Goodier Theory of Elasticity, 3rd edition, International Student Edition, McGraw-Hill 1970..
• Shames I.H., Cozzarelli F.A., Elastic and inelastic stress analysis, Prentice-Hall, 1991, ISBN 1560326867
• Love, A. E. H. (4 ed.). (1944). Treatise on the Mathematical Theory of Elasticity. Dover Publications. ISBN 0486601749.
• Marsden, J. E., & Hughes, T. J. R. (1994). Mathematical Foundations of Elasticity. Dover Publications. ISBN 0486678652.

---

ערך זה הוא קצרמר בנושא פיזיקה. אתם מוזמנים לתרום לוויקיפדיה ולהרחיב אותו.