מומנט מגנטי
מומנט מגנטי או מומנט דיפול מגנטי הוא גודל פיזיקלי שמאפיין מגנט, גופים וחלקיקים בעלי תכונות מגנטיות. מידיעת המומנט המגנטי ניתן לחשב (בקירוב) את השדה המגנטי שהמגנט יוצר רחוק מעצמו (במרחק שגדול מהממדים שלו), ואת הכוחות ומומנטי הכוח העיקריים שפועלים על המגנט כשהוא נמצא בשדה מגנטי חיצוני.
מומנט מגנטי הוא גם תכונה חשובה לאפיון חלקיקים, ובחלקיקים תת-אטומיים הוא קשור לספין שלהם.
מומנט מגנטי הוא גודל וקטורי, ומסומן בדרך כלל ב- או (בעיקר עבור חלקיקים) ב-. המוסכמה היא שכיוון הווקטור מצביע מהקוטב המגנטי הדרומי אל הצפוני.
מכיוון שככל הידוע לא יכול להיות מונופול מגנטי אלא רק דיפולים, כלומר לא יכול להיות קוטב מגנטי אחד מבודד, אלא הקטבים חייבים לבוא בזוגות, מומנט הדיפול הוא התכונה הבסיסית ביותר הקשורה למגנט (בניגוד למטען חשמלי שבסיסי יותר ממומנט הדיפול החשמלי).
נוסחאות לחישוב מומנט מגנטי[עריכת קוד מקור | עריכה]
מומנט מגנטי של לולאת זרם[עריכת קוד מקור | עריכה]
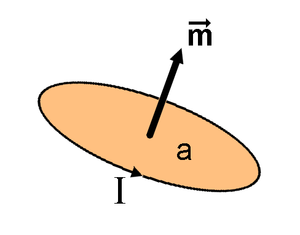
עבור לולאה שנמצאת במישור, אשר מקיפה שטח בעל גודל , ואשר על שפתה זורם זרם חשמלי , המומנט המגנטי יהיה שווה למכפלת הזרם בשטח אותו הלולאה מקיפה [1]:
כיוון המומנט המגנטי יהיה ניצב למישור הלולאה, לפי כלל יד ימין.
כאשר הלולאה אינה נמצאת במישור, אלא יש לה מבנה תלת־ממדי, אפשר להכליל את ההגדרה הזו ל:
כאשר האינטגרל הוא אינטגרל משטחי על פני כל משטח שהלולאה מהווה את שפתו (התוצאה אינה תלויה בבחירת המשטח). ניתן לראות את ההגדרה הזו כווקטור שכל אחד מרכיביו שווה למכפלת הזרם בשטח שיוצר ההיטל של הלולאה על המישור שניצב לכיוון הווקטור, כאשר יש להקפיד לחבר תרומות של משטחים שההיטל שלהם חופף.
מומנט מגנטי של התפלגות זרם כללית[עריכת קוד מקור | עריכה]
במקרה הכללי ביותר, של התפלגות זרם שרירותית במרחב, המומנט המגנטי נתון על ידי:
כאשר
- הוא אלמנט נפח, הוא וקטור המיקום של אלמנט הנפח, ו- הוא וקטור צפיפות הזרם בנקודה זו.
דיפול מגנטי[עריכת קוד מקור | עריכה]
דיפול מגנטי הוא גוף תאורטי נקודתי, שלו ניתן לייחס רק מומנט דיפול מגנטי, ואשר התכונות המפורטות להלן יהיו נכונות עבורו במדויק. עבור גופים מציאותיים תכונות אלה עשויות להיות נכונות רק בקירוב.
דיפול בשדה מגנטי חיצוני[עריכת קוד מקור | עריכה]
כאשר דיפול מגנטי בעל מומנט נמצא בשדה מגנטי אחיד , לא יפעל עליו כוח כולל, אולם השדה המגנטי יפעיל עליו מומנט כוח:
- .
מומנט הכוח יתאפס אם מומנט הדיפול הוא בדיוק בכיוון השדה (או בדיוק נגדו). בכל מקרה אחר מומנט הכוח יפעל בצורה ששואפת להביא את כיוון הדיפול להיות מקביל לכיוון השדה. כתוצאה מכך, לדיפול שנמצא בשדה תהיה אנרגיה פוטנציאלית:
- ,
כלומר המצב בו הדיפול הוא בכיוון השדה מהווה מינימום של האנרגיה, והוא מצב שיווי משקל יציב.
כאשר דיפול נמצא בשדה מגנטי בלתי אחיד, אלא תלוי במיקום, יפעל עליו כוח שרכיביו יהיו תלויים בסכום המכפלות של רכיבי מומנט הדיפול בנגזרות של רכיבי השדה המגנטי בכיוונים השונים. על עיקרון זה מבוסס למשל ניסוי שטרן-גרלך, שבו אלומה של חלקיקים בעלי ספין שונה מאפס (ולכן גם בעלי מומנט מגנטי) עוברת בשדה מגנטי לא אחיד, ומתפצלת לשתי אלומות על פי הכיוון של וקטור הספין שלהם.
השדה המגנטי הנוצר על ידי דיפול מגנטי[עריכת קוד מקור | עריכה]
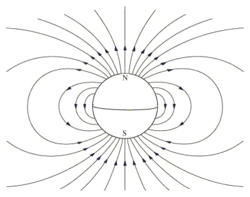
השדה המגנטי שדיפול בעל מומנט מגנטי שנמצא בראשית הצירים יוצר בנקודה במרחב ("נקודת שדה") הוא [2]:
כאשר
- הוא המרחק בין הדיפול לנקודת השדה
- הוא וקטור היחידה המצביע מהדיפול לנקודת השדה,
- הוא פרמיאביליות הריק.
גודל השדה במרחק מהדיפול, תלוי רק במרחק זה ובזווית שבין הקו המחבר את הדיפול לנקודת השדה, לבין ציר הדיפול
- ,
והוא דועך לפי .
עבור לולאת זרם ביטויים אלה יתקבלו בקירוב עבור מרחקים הגדולים מממדי הלולאה, ואז הם לא יהיו תלויים בצורתה, אלא רק במומנט הדיפול המגנטי שלה.
המומנט המגנטי של חלקיקים[עריכת קוד מקור | עריכה]
המומנט המגנטי היא תכונה חשובה שמאפיינת חלקיקים שונים, קשורה קשר הדוק לגדלים הקוונטיים של התנע הזוויתי והספין שלהם.
המומנט המגנטי של אטומים נובע ברובו מתרומה של האלקטרונים שלו. חלק מהתרומה הזו מקורה בתנועת האלקטרונים מסביב לגרעין האטום. מבחינה קלאסית ניתן לראות סיבוב של חלקיק טעון סביב נקודה מסוימת כטבעת זרם, וניתן לקשר בין המומנט המגנטי לבין התנע הזוויתי של החלקיק. המומנט המגנטי שנגרם כתוצאה מסיבוב של אלקטרון יהיה [3]:
כאשר:
- הוא התנע הזוויתי
- הוא מטען האלקטרון
- הוא מסת האלקטרון
הסיבה שכדאי לקשור את המומנט המגנטי דווקא לתנע הזוויתי, הוא שהתנע הזוויתי ממלא תפקיד חשוב בניתוח הקוונטי של מבנה האטום, והוא מקבל ערכים מסוימים בהתאם לרמות האנרגיה של האלקטרון באטום. מכיוון שערכים אלה הם כפולה של קבוע פלאנק, במספר חסר ממדים שתלוי במספרים הקוונטיים של רמות האנרגיה השונות, נוח לבטא את המומנט המגנטי של האטום בכפולות של המגנטון של בוהר [4]:
- .
גם לאלקטרון כשלעצמו יש מומנט מגנטי שנובע מהספין שלו. גם מומנט מגנטי זה פרופורציוני לספין, אולם יש לכפול אותו בעוד גודל חסר ממדים שנקרא "g-factor", ושניתן לחשבו או ניסויית, או מתוך תאוריות מתקדמות יותר ממכניקת הקוונטים הבסיסית (כגון אלקטרודינמיקה קוונטית).
המומנט המגנטי של האטום כולו מורכב ברובו מהסכום הווקטורי של המומנטים המגנטיים של האלקטרונים שבו. אולם, מכיוון שאת רובם ניתן לסדר בזוגות שבהם התנע הזוויתי הכולל של כל אלקטרון מבטל את זה של האלקטרון השני בזוג, רוב האלקטרונים לא יתרמו למומנט המגנטי הכולל. במקרים מסוימים, בהתאם לסידור האלקטרונים ברמות האנרגיה באטום, לא יהיה לאטום כלל מומנט מגנטי. במקרים אחרים רק חלק מהאלקטרונים ברמות החיצוניות יותר, שהתמלאו רק בחלקן, יתרמו למומנט הכולל של האטום. מגנט הוא חומר שבו המומנטים המגנטיים של האטומים משפיעים אחד על השני כך שהם מסתדרים באותו הכיוון, כך שלחומר כולו יש מומנט מגנטי, שהוא סכום המומנטים של כל האטומים.
לרבים מהחלקיקים התת-אטומים האחרים, כגון הפרוטון והנייטרון יש מומנט מגנטי, אולם הוא חלש בהרבה מזה של האלקטרון. לנייטרון יש מומנט מגנטי למרות שאין לו מטען חשמלי. אולם הנייטרון אינו חלקיק יסודי, והוא מורכב מחלקיקים - הקווארקים שלהם יש מטען חשמלי.
גם לגרעין האטום עשוי להיות מומנט מגנטי, שנובע בעיקר מהספינים של הפרוטונים והנייטרונים. כאמור, גם מומנט זה חלש לעומת זה שנובע מתרומת האלקטרונים, והוא אינו תורם משמעותית לתכונות המגנטיות של החומר כולו. אך גם למומנט המגנטי של הגרעין יש חשיבות, בתופעות כמו תהודה מגנטית גרעינית (NMR), ובהשפעתו על רמות האנרגיה באטום כתוצאה מהאינטראקציה בינו לבין המומנט המגנטי של האלקטרונים, השפעה שאחראית על המבנה העל-דק (Hyperfine structure) של רמות האנרגיה (ונמדדת בסדר גודל של 10-4 eV).
ראו גם[עריכת קוד מקור | עריכה]
הערות שוליים[עריכת קוד מקור | עריכה]




























