משפט נורטון

משפט נורטון למעגלים חשמליים ליניאריים קובע שכל צירוף של מקורות מתח, מקורות זרם ונגדים בעלי שני הדקים שקול חשמלית למקור זרם יחיד ונגד יחיד המחובר אליו במקביל. עבור מעגלי AC הפועלים בתדירות יחידה המשפט ניתן ליישום גם לגבי אימפדנסים כלליים, ולא רק לנגדים. שקול נורטון משמש לייצוג כל רשת של מקורות ואימפדנסים ליניאריים בתדירות נתונה. המעגל כולל מקור זרם אידיאלי במקביל לאימפדנס אידיאלי (או נגד למעגלים לא ריאקטיביים).
משפט נורטון הוא הרחבה של משפט תבנין והוא הוצג ב-1926 בנפרד על ידי שני אנשים: החוקר האנס פרדיננד מאייר (1895-1980) והמהנדס אדוארד לארי נורטון (1898-1983) ממעבדות בל.
חישוב שקול נורטון[עריכת קוד מקור | עריכה]
במציאת שקול נורטון יש להבחין במעגל המקורי בין חלק המעגל שאותו רוצים להחליף בשקול, לבין חלק המעגל המוגדר כעומס, ואותו אין מחליפים. העומס אינו משפיע על השקול המתקבל, וההשפעה היחידה שלו היא בצורת החיבור של שני הדקיו לחלק המעגל שאותו מחליפים. לעיתים (כמו בציור שלעיל), העומס אינו מופיע במפורש, אבל הדקיו חייבים להיות מוגדרים בצורה ברורה.
כדי לחשב את המעגל השקול יש לבצע את השלבים הבאים:
- חישוב זרם ההדקים בתנאי קצר, כלומר כאשר ההדקים מקוצרים - התנגדות אפס. זהו .
- חישוב מתח ההדקים בתנאי נתק, כלומר כאשר לא מחובר נגד עומס בין ההדקים - התנגדות אינסופית. זהו . מחשבים לפי:
המעגל השקול הוא מקור זרם שזורם דרכו במקביל לנגד שהתנגדותו .
את תנאי 2 ניתן גם לחשב באופן הבא:
- 2א. החלפת מקורות מתח אידיאליים בקצר ומקורות זרם אידיאליים בנתק. מקורות בעלי התנגדות פנימית מוחלפים בהתנגדות הפנימית שלהם.
- 2ב. חישוב ההתנגדות הכוללת של המעגל בין שני ההדקים. זהו .
דוגמה[עריכת קוד מקור | עריכה]
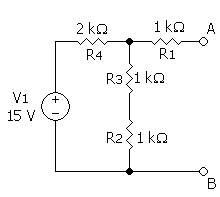
 |
 |
 |
סך הזרם נתון על ידי:
חישוב הזרם השקול, כלומר הזרם דרך העומס, תוך שימוש במחלק זרם:
חישוב ההתנגדות השקולה:
המרה משקול תבנין[עריכת קוד מקור | עריכה]
שקול תבנין כולל מקור מתח ונגד המחובר אליו בטור.
שקול תבנין קשור לשקול נורטון על ידי המשוואות הבאות:















