פוטואלסטיות

פוטואלסטיות היא שיטה פיזיקלית אופטית המאפשרת איסוף מידע אודות הפיזור או הפילוג של מאמצים ומעוותים (עיבורים) במבנה על פני שטחים, בניגוד למדידות נקודתיות באמצעות מד עיבור. השיטה מסתמכת על כך שבחומרים שקופים מסוימים מהירות האור ובהתאם גם מקדם השבירה של האור, תלויים ברמת המאמץ או המעוות (עיבור). אם המאמץ בכיוונים שונים אינו אחיד, תתקבל שבירה כפולה. תחת אור מקוטב נוצרת התאבכות בין רכיבים של גלי האור שהתקדמו במהירות שונה ומתקבלת תמונת פסים. אור לבן יוצר פסים בכל צבעי הקשת, אור מונוכרומטי ייצור פסים כהים ובהירים לסירוגין. ככל שהמאמץ בחומר הפוטואלסטי גדול יותר כן גדל מספרם של מחזורי הצבעים. הפוטואלסטיות מיישמת את התופעה הזו לצורך אנליזה ניסויית של מאמצים ועיבורים וככזו היא כלי חשוב ליישום תורת חוזק חומרים ומסייעת לתיכון מבנה שצורתו הגאומטרית מאפשרת חלוקה טובה יותר של עומסים, וכתוצאה - מבנה עמיד יותר.
השם הוא צירוף של המילים היווניות פוטו שמשמעה אור ואלסטיות.
היסטוריה[עריכת קוד מקור | עריכה]
תופעת השבירה הכפולה והקשר בינה ובין המאמצים והעיבורים נתגלתה לראשונה על ידי הפיזיקאי הסקוטי דייוויד ברוסטר[1][2]. ממצאיו של ברוסטר היו בסיס לעבודות דומות של אוגוסטן ז'אן פרנל ושל ג'יימס קלארק מקסוול[3]. החל משנות הארבעים של המאה ה-20 יושם הידע הזה כאמצעי למחקר לפיתוח תורת חוזק חומרים[4] [5] [6] [7] [8]. התפתחות בתורת חוזק חומרים יחד עם יישום נרחב של פוטואלסטיות, השפיעו במיוחד על התפתחות המטוסים בשנות ה-40 וה-50 של המאה ה-20. השיפורים הניכרים שחלו במבנה מטוסים ובביצועיהם נבעו, בין השאר משיפור בחומרי המבנה ובגאומטריה של המבנה. בשנים שלאחר מלחמת העולם השנייה הופיעו מטוסים עם מבנה קל מאוד יחסית למשקלם. מבנה כזה רגיש להעמסה מחזורית, הגורמת לעייפות החומר, יותר מאשר להעמסה סטטית, ולכן השיטות הישנות והפשוטות להוכחת העמידות של מבנה – העמסה הדרגתית עד כשל - אינן מספקות, משום שאופן הכשל ומקומו שונים. הפוטואלסטיות, בהיותה שיטה המאפשרת כיסוי שטחים שלמים, מאפשרת זיהוי האזורים שבהם צפוי כשל התעייפות. בשנות ה-60 וה-70 של המאה ה-20 שימשה הפוטואלסטיות כלי עזר לפיתוח שיטות ממוחשבות לאנליזת מאמצים ובעיקר שיטת אלמנטים סופיים [9] בשנים אלו כמעט כל מפעל מטוסים גדול החזיק מעבדה פוטואלסטית. בשנות ה-80 החלה ירידה בהיקף השימוש בפוטואלסטיות בגלל השיפור ביכולות ובזמינות של מחשבים ותוכנות לניתוח מאמצים. אולם בגוש המזרחי, בגלל נחיתות ביישומי מחשב, הייתה התפתחות ניכרת של הפוטואלסטיות. כמעט בכל בית ספר להנדסה בעולם נעזרים בפוטואלסטיות לצורך הדגמה של חלוקת מאמצים ולימוד חוזק חומרים. בישראל פעלו מספר מעבדות פוטואלסטיות. בטכניון בראשות הפרופ' אברהם בצר, באוניברסיטת תל אביב בראשות הפרופ' מירצ'ה ארקאן ובמכון ויצמן בראשות הפרופ' דניאל וגנר. כמו כן פעלו בישראל מעבדות פוטואלסטיות בתעשייה האווירית, ברפא"ל, ובסניף הישראלי של חברת וישיי.
הסבר השיטה[עריכת קוד מקור | עריכה]
האור (בתחום הנראה לעין האנושית) הוא קרינה אלקטרומגנטית בתחום אורכי הגל 0.4 עד 0.8 מיקרון. התקדמות האור כרוכה בתנודה של השדה החשמלי והשדה המגנטי, וקטורי השדה החשמלי והמגנטי מאונכים לכיוון התקדמות האור. בדרך כלל מקורות אור מפיקים תנודות לכל הכיוונים. הכנסת מקטב בציר התקדמות האור מאפשרת מעבר לרכיב אחד בלבד של התנודה – זה המקביל למישור הקיטוב.
היחס בין מהירות האור בריק c לבין מהירותו בתוך חומר כלשהו נקרא מקדם השבירה. בחומרים רבים היחס הזה תלוי ברמת המאמץ או העיבור (באנגלית strain) שבחומר. לצורך מדידות פוטואלסטיות נבחרו או פותחו חומרים שבהם היחס הזה הוא ביחס ישר לרמת המעוות.
כאשר קרן אור מקוטב מתקדמת בחומר שקוף, תנודות השדה החשמלי תהיינה בהתאמה למקדם השבירה. הרכיבים המקבילים למאמצים הראשיים x ו-y יתקדמו במהירויות ו-, בהתאמה:
ו-.
לאחר שהקרן עברה חומר בעובי נוצר הפרש פאזה בין שני הרכיבים ששיעורו
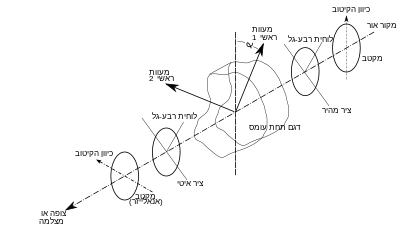
בפולריסקופ העברה כגון זה שבתרשים 1, מתקיים
כאשר K הוא תכונה פיזיקלית של החומר הנקראת מקדם המעוות (או העיבור) הפוטואלסטי (strain optical coefficient) המקיים את היחס
ובהתאם
בתרשים מופיעים אינדקסים 1 ו-2 במקום x ו-y כדי להבהיר שאין קשר למערכת צירים של מתקן הניסוי או הפולריסקופ.
בפולריסקופ החזרה, כגון זה שבתרשים 2 ו-3 נוסף פקטור 2, כי קרן האור עוברת פעמיים את עובי החומר.
פולריסקופ החזרה מיועד לדגמים שעליהם יושם ציפוי מחומר פוטואלסטי בהדבקה באמצעות דבק מחזיר אור.
עוצמת האור לאחר שעבר בחומר הפוטואלסטי ובפולריסקופ קווי:
= הזווית בין קו הקיטוב ובין כיוון המעוותים הראשיים
מתקיים כאשר שני המקטבים ניצבים זה לזה ובו-זמנית הם גם מקבילים לכיווני המעוות הראשיים בחומר. באזור יתקבל פס שחור ועל ידי סיבוב המקטבים ניתן למצוא את כיווני המעוות בחומר.
בפולריסקופ מעגלי (תרשים 1) מוכנסות שתי לוחיות גל במסלול האור, סמוך למקטבים, אחת מכל צד של הדגם הנבדק. הלוחיות הן בעלות ערך של רבע אורך גל. אור לבן מחושב כאילו היה בעל אורך גל של 0.57 מיקרון, הערך המדויק נקבע לפי ספקטרום מקור האור ולפי רגישות המצלמה. עצמת האור ביציאה מהפולריסקופ המעגלי:
ממשוואה זו רואים שעוצמת האור היא אפס בכל מקום שבו היא כפולה שלמה של אורך הגל (N הוא מספר שלם) המספר N נקרא "סדר הפס" (fringe order) ערכים לא שלמים של N ניתן למדוד בדרכים הבאות:
- לפי הגוונים האופייניים. בין סדר פס אפס לסדר פס 1 מופיעים כל צבעי הקשת, אם כי בהירותם הולכת ונחלשת עם עליית סדר הפס (ראו תצלום 1)[10]
- מדידה באמצעות לוחית גל מתכווננת (Babinet-Soleil Null Balance Compensator או Wollaston Prism - האחרון שימושי במיוחד בתחום התת-אדום)
ס# למדוד על ידי שינוי הכיוון של המקטבים ולוחית הגל (שיטת TARDY)
דגמים פוטואלסטיים[עריכת קוד מקור | עריכה]
ציפוי פוטואלסטי[עריכת קוד מקור | עריכה]
השיטה הנפוצה ביותר היא ציפוי פוטואלסטי. ציפוי של חומר מתאים מיושם לרוב על מבנה אמיתי או חלק ממנו, ואת המבנה הזה בוחנים באמצעות פולריסקופ החזרה. על המבנה מפעילים עומסים המייצגים את עומסי השרות שלו.
דגמים דו-ממדיים[עריכת קוד מקור | עריכה]
אלו מיועדים לפולריסקופ העברה. אפשר להשתמש גם בפולריסקופ החזרה ואז אחד מצידי הדגם יצופה בחומר מחזיר אור. PVA (פוליוויניל אלכוהול) מעורבב באבקת אלומיניום, מהווה ציפוי מוצלח משום שברק ההחזרה הוא מט, וקל לקלף ציפוי כזה ללא נזק לדגם.


דגמים תלת-ממדיים דקים[עריכת קוד מקור | עריכה]
ניתן במקרים רבים לייצר דגם תלת-ממדי ולבחון אותו בפולריסקופ רגיל, בהנחה שפיזור המאמצים הוא דו-ממדי, הדבר יהיה נכון עבור מבנים שצורתם היא צירוף של אלמנטים דקים, או שהמשטחים שלהם מקבילים זה לזה.
דגמים תלת-ממדיים[עריכת קוד מקור | עריכה]
יישום פוטואלסטיות למבנה תלת-ממדי בעל צורה מורכבת הוא מסובך ויקר, ולכן כמעט אינו נמצא כיום בשימוש.


יישומים ושימושים[עריכת קוד מקור | עריכה]
- לימוד והבנת התנהגותו של מבנה לצורך חישוב מאמץ בשיטות קלאסיות או הכנת מודל מתמטי ואנליזה ממוחשבת
- ניתוח ניסויי של מבנים הקשים לניתוח תאורטי
- מציאת מקדמי ריכוז מאמצים[11]
- אופטימיזציה של מבנה על מנת להשיג יחס גבוה יותר בין החוזק לבין המשקל והמחיר[12]
- בדיקה תכונות, איכות ייצור והרכבה של מבנים שקופים. בדיקה כזו היא בדרך כלל ללא הרס[13]
- בדיקת תהליכי ייצור של רכיבי מיקרואלקטרוניקה, סיליקון וגרמניום אטומים לאור נראה, ולכן משתמשים בגלאים ומקטבים המתאים לתחום התת-אדום[14][15]
- איתור מיקום אופטימלי ליישום של אמצעי מדידה אחרים, כגון : מדי-עיבור, אמצעים לזיהוי סדק, מדי-שקיעה ועוד
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Dally J.W. & Riley W.F., Experimental Stress Analysis, 2nd Ed.McGraw-Hill 1987 p. 343 ISBN 0-07-015204-7
- Hecht E., Optics, Schaum McGraw-Hill 1975, ISBN 0-07-027730-3, pp. 3-4, 93-117
- Zandman F., Redner S., Dally J.W., Photoelastic Coatings, The Iowa State University + Society for Experimental Stress Analysys, 1977. ISBN 0-8138-0035-8
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- פוטואלסטיות, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ D. Brewster, Experiments on the depolarization of light as exhibited by various mineral, animal and vegetable bodies with a reference of the phenomena to the general principle of polarization, Phil. Tras. 1815, pp.29-53
- ^ D. Brewster, On the communication of the structure of doubly-refracting crystals to glass, murite of soda, flour spar, and other substances by mechanical compression and dilation, Phil. Tras. 1816, pp.156-178
- ^ Timoshenko s.p., History of Strength of Materials, Dover 1983, p.249, 271, 351 ISBN 0-486-61187-6
- ^ Timoshenko S.P. & Googier J.N., Theory of Elasticity, 3rd Ed., Mc-Graw Hill 1970, pp.115, 150-164
- ^ Den Hartog, Advanced Strength of Materials, McGraw-Hill 1952, p.199
- ^ Timoshenko S.P. & Woinowsky-Krieger S.,Theory of Plates and Shells, McGraw-Hill 1970, p.362 ISBN 0-07-085820-9
- ^ אטינגן שלמה, עורך, מדריך לאינג'ינר, כרך ראשון מדעי היסוד, מסדה תשכ"ה, ע' 224
- ^ Young W.C., Roark's Formulas for stress and Strain, 6th ed., McGraw-Hill 1989 pp.51-58 ISBN 0-07-072541-1
- ^ Sanford R.J. & Beaubien L.A., Stress Analysis of a Complex Part: Photoelasticity V.S. Finite Element, Experimental Mechanics Dec.1977
- ^ אבי פן, צילום באור מקוטב כאמצעי לאנליזת חוזק ומבנים בשיטה הפוטואלסטית, עבודת גמר הנדסאי, מכללת קריית-אונו, המגמה לצילום, 1984
- ^ Peterson R.E.,Stress Concentration Factors, John Wiley 1974 ISBN 0-471-68329-9
- ^ Macke H.J. & Sant T.D., The Intricate Pattern of Stress, Mechanical Engineering, Dec 1982
- ^ רייס מ., מדריך להנדסה אזרחית, מסדה 1990, ע'325
- ^ Williams P.A.,Rose, Lee, Conrad, Day and Hale, Optical, thermo-optic, electro-optic and photoelastic properties of bismuth germanate, Applied Optics, Vol.35, No.19, July1996 pp.3562-3569
- ^ Anand Asundi, Recent Advances in Photoelastic Applications, Nanyang Technological University, Singapore 2008

















