פרדוקס קו החוף
פרדוקס קו החוף הוא האבחנה הלא אינטואיטיבית כי לא ניתן להגדיר היטב את אורכו של קו חוף. הפרדוקס תקף גם לגבולות גאוגרפיים אחרים בעלי אופי דומה. מקור הפרדוקס הוא באופי הפרקטלי של קווי חוף. הפרדוקס נבחן לראשונה על ידי לואיס פרי ריצ'רדסון והעסיק גם את בנואה מנדלברוט כשהחל לפתח את תורת הפרקטלים.
הבחנה ראשונה היא כי אורכו של קו חוף תלוי באורך ה"סרגל" בו משתמשים כדי למדוד. סרגל הוא ישר ולא ניתן להשתמש בו כדי למדוד פיתולים הקטנים יותר מאורכו. לכן ככל שהסרגל קצר יותר, נמדדים יותר פיתולים ובהתאם אורכו של קו החוף מתארך. אולם דבר זה כשלעצמו אינו אומר כי אין לקו חוף אורך בר הגדרה. אם ננסה לדוגמה למדוד את היקפו של מעגל מושלם עם קוטר של מטר באמצעות סרגל, תתרחש תופעה דומה. ככל שנשתמש בסרגלים קצרים יותר האורך הנמדד יתארך, אולם ההתארכות תהיה חסומה, ותלך ותתקרב להיקף האמיתי של המעגל שהוא (פאי) מטרים. תופעה דומה תתרחש בכל צורה מוכרת מן הגאומטריה האוקלידית. עם זאת, התופעה אינה קורית כאשר עוסקים בקווי חוף. הסיבה נעוצה בעובדה כי לא משנה עד כמה נבחן קו חוף מקרוב, תמיד נמצא בו פיתולים זעירים הדומים לפיתולים הגדולים בהם מבחינים בבחינה מרחוק (בשונה מכל צורה גאומטרית אוקלידית). בשל כך במקום שהאורך הנמדד ילך ויתקרב לערך מדויק ככל שהסרגלים מתקצרים, הרי שהאורך רק הולך וגדל לאינסוף. כלומר אם רק נשתמש בסרגל קטן מספיק, נוכל למדוד אורך ארוך יותר מכל מספר שנרצה. מכאן שאורך קו החוף הוא אינסופי.
בפועל יש גבול פיזיקלי להשפעתו של הפרדוקס מכיוון שהגדרת אורכים של עצמים עשויים חומר כאשר הסרגל באורך תת-אטומי בעייתית בפני עצמה.
אם רוצים למדוד אורך של קו חוף ולקבל תוצאה סופית, יש צורך לקבוע אורך מספק של סרגל כך שפיתולים קטנים ממנו לא ימדדו. במקרה כזה בעייתי להשוות בין אורכיהם של קווי חוף שונים משום שבחירת אורך הסרגל משפיעה על יחס האורכים ביניהם. למשל קו החוף המפורץ ושופע הפיורדים של נורווגיה גורם לכך שהקטנה זעירה של הסרגל, מאריכה משמעותית את האורך הנמדד. לעומת זאת אורך קו החוף הישר יחסית של ישראל גורם לכך שלהקטנה של הסרגל השפעה קטנה יותר על האורך הנמדד. בשל כך, אם נשווה את אורך קו החוף של נורווגיה לזה של ישראל, היחס ביניהם רק ילך ויגדל ככל שנקטין את הסרגל ולא ישמור על ערך קבוע.
היסטוריה[עריכת קוד מקור | עריכה]
במהלך מחקריו של לואיס פרי ריצ'רדסון על השפעת האורך של גבול בין מדינות על הסיכויים להתפתחות מלחמה ביניהן, שם ריצ'רדסון לב כי הפורטוגזים דיווחו כי אורך הגבול המשותף שלהם עם ספרד הוא 987 ק"מ, בעוד הספרדים דיווחו כי אורכו 1,214 ק"מ. ריצ'רדסון הבין כי השוני בנתונים נובע משימוש בסרגלים שונים ופרסם ב-1951 תיאור מתמטי של התארכות הגבול כפונקציה של אורך הסרגל (תוצאה הקרויה על שמו "אפקט ריצ'רדסון").
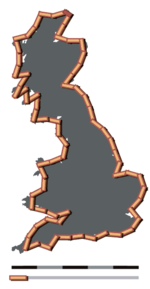
בשנת 1967 פרסם בנואה מנדלברוט מאמר במגזין Science שכותרתו How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. במאמר תיאר מנדלברוט את אפקט ריצ'רדסון והרחיב את הדיון המתמטי בו. ב-1975 טבע מנדלברוט את המונח "פרקטל" לתיאור צורות בעלי תכונות דומות.
ניתוח מתמטי[עריכת קוד מקור | עריכה]

ההתייחסות האינטואיטיבית לקו חוף היא כעקומה חד-ממדית. אולם בחינה מעמיקה תגלה כי הנחה זו שגויה. קו חוף הוא למעשה פרקטל, שיש לו ממד שברי שבין 1 ל-2. ככל שהממד של העקומה קרוב יותר ל-1, כן היא יותר חלקה ודומה לעקומות החד-ממדיות המוכרות מהגאומטריה האוקלידית. ככל שהממד קרוב יותר ל-2, העקומה "מתנודדת" יותר, וכוללת פיתולים קיצוניים בכל קנה מידה, והיא דומה לעקום פאנו שהוא למעשה פרקטל דו-ממדי. בפועל, לקווי חוף יש ממד שברי שאינו גדול בהרבה מ-1. באמצעות הגדרתו של פליקס האוסדורף לממד שברי, ניתן להעריך את הממד השברי של קווי חוף שונים. מנדלברוט השתמש בהגדרה כדי להצדיק את החישובים שערך ריצ'רדסון, וכדי להעריך קירובים לממדיהם של קווי חוף שונים. התוצאות שהתקבלו נעו בין 1.02 לקו החוף של דרום אפריקה, ועד 1.25 לקו החוף המערבי של בריטניה. בהערכה מאוחרת יותר נמדד ממד שברי מקורב של 1.52 בקו החוף של נורווגיה.
באמצעות כלים אלו מתורת הפרקטלים הוכיח מנדלברוט בכלים תאורטיים את אפקט ריצ'רדסון, אותו הסיק ריצ'רדסון על סמך אמצעים אמפיריים. אורכו של קו חוף כפונקציה של אורך הסרגל () עומד ביחס ישר לאורך הסרגל (), בחזקת אחד פחות הממד השברי של קו החוף (): .
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- פרדוקס קו החוף, באתר MathWorld (באנגלית)