גל אינרציאלי
יש להשלים ערך זה: בערך זה חסר תוכן מהותי.
| ||
| יש להשלים ערך זה: בערך זה חסר תוכן מהותי. | |
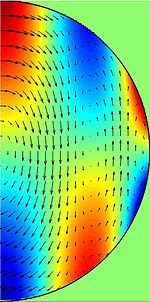
במכניקת הזורמים ומדעים פלנטריים, גלים אינרציאליים, שידועים גם בשם תנודות אינרציאליות, הם סוג של גלים מכניים שקיומם מתאפשר בזורמים מסתחררים. הם מייצגים שינויים מתקדמים בשדה הווקטורי של מהירויות פרודות הזורם כפי שאלו נצפות במערכת קואורדינטות המסתובבת ביחד עם הזורם. בשונה מגלי שטח כבידתיים הנצפים בחוף הים או באמבטיה, גלים אינרציאליים מתקדמים בתוך פנים הזורם, ולא על פני השטח שלו. כמו כל סוג גל אחר, התקדמותו של גל אינרציאלי מתאפשרת אודות לכוח מחזיר השואף להחזיר את מצבו הפיזיקלי של הזורם לקדמותו; בגלים אינרציאליים, הכוח המחזיר הוא כוח קוריוליס, כוח מדומה המורגש אך ורק במערכות ייחוס מסתובבות. גלים אינרציאליים נקראים כך משום שהכוח המניע אותם הוא כוח קוריוליס, שהוא כוח אינרצי, דהיינו כוח הנובע מהאינרציה של הזורם ומתאוצת מערכת הקואורדינטות בלבד.
גלים אינרציאליים נצפים באטמוספירה, באוקיינוסים, באגמים ובניסויי מעבדה. גלי רוסבי, זרמי ים גאוסטרופיים, ורוחות גאוסטרופיות הן דוגמאות לגלים אינרציאליים (שתי הדוגמאות האחרונות מתייחסות לגלים אינרציאליים עם תדירות אפס). קרוב לוודאי שגלים אינרציאליים מתקיימים גם בליבה המותכת של כדור הארץ המסתובב. הבנת התנהגותם של גלים אינרציאליים בתחומים סגורים עשויה לסייע גם בחקר והגברת יציבותם של כלי תחבורה אוויריים; מכיוון שנוזלים אינם מתנהגים כגוף קשיח, כאשר מכלי הדלק של אלו קרובים למלוא קיבולת הדלק שלהם כל שינוי בקצב העלרוד, הסבסוב או הגלגול (תאוצה זוויתית) של כלי הטיס גורם להיווצרותם של גלים אינרציאליים בדלק הנוזלי (הדינמיקה של נוזל בתוך כלי קיבול מכונה "Slosh dynamics"(אנ')).
סקירה היסטורית[עריכת קוד מקור | עריכה]
החקירה הראשונה של תנודות וגלים המתקדמים באמצעות היציבות הפנימית של זורם מסתובב נערכה על ידי לורד קלווין ב-1880, בעבור גאומטריה גלילית. מאוחר יותר, אנרי פואנקרה, אלי קרטן ואחרים חקרו תנועות דומות עבור גאומטריה ספרואידית. Bjerknes ושותפיו גילו מחדש באופן בלתי תלוי את התנודות תלויות הסיבוב הללו, וכינו אותן תנודות "אלסטו-אינרציאליות". חלק ניכר מהעבודות המוקדמות הללו קובץ במונוגרפיה של Harvey P. Greenspan מ-1968 - "התאוריה של זורמים מסתובבים", בה נידונים הן גלים אינרציאליים בזורמים לא חסומים והן מודי תנודה אינרציאליים בתחומים חסומים. לאחרונה נעשתה התקדמות תאורטית לא מבוטלת לקראת מציאת פתרונות מפורשים למודי תנודה אינרציאליים בעבור כלי קיבול בצורות גאומטריות אחדות.
כוח מחזיר[עריכת קוד מקור | עריכה]
תבניות וקטורי המהירות אותן מייצגים גלים אינרציאליים מוחזרות למצב שיווי משקל על ידי כוח קוריוליס, שהוא תוצאה של סיבוב המערכת. תאוצת קוריוליס (יחד עם הכוח הצנטריפוגלי) מופיעה במערכת מסתובבת כדי לפצות על העובדה שמערכת ייחוס כזאת מאיצה כל העת. גלים אינרציאליים, לפיכך, לא יכולים להתקיים ללא סיבוב. כוח קוריוליס הוא מורכב וקשה יותר להבנה ממתיחות במיתר, שכן הוא פועל תמיד בניצב לכיוון התנועה, וחוזקו תלוי בקצב הסיבוב של המערכת ובמהירות הפרודה כפי שנצפית במערכת המסתובבת. תכונות אלו של כוח קוריוליס מוליכות למאפיינים הייחודיים של גלים אינרציאליים.
מאפיינים[עריכת קוד מקור | עריכה]
העובדה שבמערכות ייחוס מסתובבות ישנו כיוון מועדף מסוים (ציר הסיבוב) מכתיבה התנהגות פיזיקלית אי-איזוטרופית לגלים אינרציאליים; מסיבה זו לגלים אלו תכונות ייחודיות, ובין היתר תדירותם תלויה אך ורק בכיוון התקדמותם. כמו כן חוק ההחזרה, לפיו גל מוחזר באופן כזה שזווית הפגיעה שווה לזווית ההחזרה, אינו תקף לגלים אינרציאליים; במקום זאת, הם מוחזרים באופן שמשמר את הזווית בין כיוון התקדמותם לציר הסיבוב.
בדומה לגלי אור, גלים אינרציאליים הם גלים רוחביים, כלומר התנודות שהם מייצגים מתחוללות בניצב לכיוון התקדמות הגל. הקיטוב שלהם הוא קיטוב מעגלי. תכונה גאומטרית ייחודית אחת של גלים אינרציאליים היא שמהירות המופע שלהם, שמתארת את ההתקדמות של נקודות השיא והשפל של הגל, היא ניצבת למהירות החבורה, שמתארת את קצב וכיוון העברת האנרגיה. ההסבר לכך הוא שתדירות הגל תלויה אך ורק בכיוונו של וקטור הגל (שהוא גם כיוון מהירות המופע) ולא בערכו המוחלט של וקטור הגל[א]; לפיכך, הנוסחה למהירות החבורה, , אינה מתאפסת רק עבור שינויים זעירים בוקטור הגל הניצבים לכיוונו הנוכחי - ולכן מהירות החבורה ניצבת לוקטור הגל!
בעוד שבגלי קול או גלים אלקטרומגנטיים כל תדירות אפשרית, תדירותם של גלים אינרציאליים יכולה לקבל ערך בטווח שבין אפס לפעמיים המהירות הזוויתית של מערכת הזורם. כפי שצוין מקודם, תדירותם נקבעת על ידי כיוון התקדמותם. לגלים הנעים לגמרי במישור הניצב לציר הסיבוב יש תדירות אפס והם מכונים מודים גאוסטרופיים. לגלים הנעים במקביל לציר הסיבוב יש תדירות מרבית (פעמיים תדירות הסיבוב), ולגלים בזוויות ביניים יש תדירויות ביניים. במרחב החופשי (ללא קצוות המכתיבים תנאי שפה), גלים אינרציאליים יכולים להתקיים בכל תדירות בין 0 ופעמיים קצב הסיבוב. מיכל סגור, לעומת זאת, מכתיב אילוצים על התדירויות האפשריות של גלים אינרציאליים, כמו בכל סוג גלים אחר[ב]. גלים אינרציאליים במיכל סגור מכונים לעיתים קרובות מודים אינרציאליים. במיכל כדורי, למשל, המודים האינרציאליים מהווים אוסף בדיד של תדירויות, מה שמותיר מרווחי תדירות אותן גלים אינרציאליים לא יכולים לקבל.
דוגמאות לגלים אינרציאליים[עריכת קוד מקור | עריכה]
כל סוג של זורם יכול לאפשר גלים אינרציאליים: מים, שמן, מתכות נוזליות, אוויר, או גזים אחרים. גלים אינרציאליים נצפים בשכיחות הגבוהה ביותר באטמוספירות פלנטריות (גלי רוסבי, רוחות גאוסטרופיות), ובאוקיינוסים ובאגמים (זרמים גאוסטרופיים), שם פעולתם אחראית למרבית הערבוב שמתרחש. באוקיינוגרפיה פיזיקלית, לגלים פנימיים (internal waves) בעלי זמן מחזור ארוך ביותר- שהוא בר- השוואה ליממה ארצית - מתייחסים כגלים שנמצאים קרוב לגבול האינרציאלי (near-inertial waves); כלומר אלו גלים שהמכניזם העיקרי המניע אותם הוא אפקט קוריוליס. גלים פנימיים עם זמן מחזור קצר יותר מושפעים הן מהכבידה והן מאפקט קוריוליס, ולכן הם נקראים גלי כבידה-אינרציאליים. כמו כן, גלים אינרציאליים המושפעים מהשיפוע של קרקעית האוקיינוס נקראים לעיתים גלי רוסבי.
גלים אינרציאליים ניתנים לצפייה בניסויי מעבדה או בזרימות תעשייתיות, ולמעשה בכל מקום בו מבצעים תהליך הכרוך בסחרור זורמים. קרוב לוודאי שהם קיימים גם בליבה הנוזלית של כדור הארץ, ובדומה לכך, התאוריה שלהם רלוונטית גם להבנת תהליכים אסטרונומיים כמו הזרימה בדיסקות ספיחה, טבעות פלנטריות, וגלקסיות.
תיאור מתמטי[עריכת קוד מקור | עריכה]
זרימת זורם בנוכחות גל אינרציאלי נשלטת על ידי משוואות נאוויה-סטוקס במערכת ייחוס מסתובבת. מהירות הזורם של זורם עם צמיגות תחת לחץ ואשר סובב בקצב , משתנה לפי הזמן בהתאם למשוואה הדיפרנציאלית:
האיבר הראשון באגף ימין הוא גרדיאנט הלחץ, השני מתייחס לדיפוזיה צמיגית והשלישי הוא איבר קוריוליס.
למען הדיוק, היא מהירות הזורם כפי שנצפית במערכת הייחוס המסתובבת. כיוון שמערכת ייחוס מסתובבת היא מערכת מאיצה (מערכת ייחוס לא אינרציאלית), שני כוחות מדומים נוספים צצים כתוצאה מטרנספורמציית הקואורדינטות הזאת: הכוח הצנטריפוגלי וכוח קוריוליס. במשוואה לעיל, הכוח הצנטריפוגלי כבר נכלל באיבר המתייחס לגרדיאנט של הלחץ המוכלל , כלומר, קשור ללחץ הרגיל על ידי המרחק מציר הסיבוב:
במקרה שקצב הסיבוב גבוה, איבר קוריוליס ואיבר הכוח הצנטריפוגלי גדולים משמעותית בהשוואה לאיברים האחרים. מכיוון שהם קטנים בהשוואה לאלו, איבר החיכוך הצמיגי ואיבר "הנגזרת ההסעתית" (האיבר השני באגף שמאל) ניתנים להזנחה. כעת ניקח את הרוטור של שני האגפים; מכיוון שאגף ימין של המשוואה הדיפרנציאלית יהיה הרוטור של גרדיאנט הלחץ (הלחץ הוא פונקציה סקלרית של המרחב), הוא חייב להתאפס. כדי לפשט את אגף שמאל, ניעזר בזהות הווקטורית הבאה לרוטור של המכפלה הווקטורית של ו-:
מכיוון שהזורם אי-דחיס, הדיברגנץ של שדה המהירויות, , מתאפס בכל נקודה. כמו כן שני האיברים המכילים פעולות גזירה של מתאפסים היות שזהו וקטור קבוע. לפיכך כל האיברים בזהות הווקטורית נופלים פרט לאחד, מה שמניב את התוצאה:
המשוואה האחרונה מתארת את ההתפתחות בזמן של ערבוליות הזורם . כעת ניקח רוטור ונגזרת לפי הזמן של שני האגפים פעם נוספת, ונקבל, תוך שימוש בעובדה ש- בעבור זרימה אי-דחיסה, את המשוואה הדיפרנציאלית החלקית הבאה:
שימוש בתוצאה הקודמת פעם נוספת מוביל למשוואת הגלים בעבור הפרעות בשדה המהירויות:
זוהי משוואת הגל האינרציאלי בזורם מסתובב.
כדי למצוא את הקשרים המתמטיים בין המאפיינים השונים של הגל, נציב במשוואת הגל האינרציאלי את הצורה המתמטית של גל מישורי, , ונקבל:
וכך נגלה כי הפתרונות נדרשים להיות בעלי תדירות שמקיימת את יחס הנפיצה
כאשר היא הזווית בין ציר הסיבוב וכיוון התקדמות הגל.
יחס הנפיצה נראה דומה מאוד לאיבר קוריוליס במשוואת נאוויה-סטוקס במערכת מסתובבת - שימו לב לקצב הסיבוב ולפקטור 2. יחס הנפיצה מגדיר מיידית את מנעד התדירויות האפשריות בעבור גלים אינרציאליים, כמו גם את תלות תדירותם בכיוון התקדמותם.
התקדמות גלים אינרציאליים במרחב[עריכת קוד מקור | עריכה]
מהירות המופע (המהירות והכיוון שבה נקודות השיא והשפל נעות) היא בכיוון וקטור הגל :
בשונה מכך, מהירות החבורה (המהירות והכיוון שבה האנרגיה מועברת) היא הנגזרת של ביחס ל-:
הנוסחה האחרונה מתקבלת מגזירה של ביחס לשינוי בוקטור הגל הניצב לוקטור הגל . נשים לב גם שבעבור k נתון, הגודל נשמר ומקיים:
מסקנה מעניינת מן הביטויים האחרונים הוא שכאשר התדירות של הגלים האינרציאליים נמוכה מאוד אז מהירות החבורה היא בקירוב מקבילה לציר הסיבוב, כך שהמידע על הפרעות איטיות מועבר בכיוון הזה. זהו המכניזם העומד ביסוד ומתווך את היווצרותם של "עמודי טיילור", תופעה במסגרתה תנועות איטיות בזורם נוטות להיות אינווריאנטיות תחת הזזה במקביל לציר הסיבוב בזורם המסתחרר במהירות.
פירוש איכותי של התיאור המתמטי[עריכת קוד מקור | עריכה]
במרחב חופשי נטול גבולות (ללא קצוות), גל אינרציאלי מתקדם מייצג תבנית של וקטורי מהירות וערבוליות (של שדה המהירות) המשתנה במרחב ובזמן. אגף ימין של המשוואה המרכזית, , הוא לא אחר מאשר כפול הנגזרת הכיוונית של השדה בכיוון ציר הסיבוב (שנתייחס אליו כאל ציר z), דהיינו . אגף שמאל של המשוואה המרכזית מייצג את קצב השינוי (הנגזרת הזמנית) של וקטור הערבוליות של שדה המהירויות, בנקודה נתונה. מכיוון ששדה המהירויות של זורם בלתי-דחיס הוא שדה וקטורי סולנואידי על פי הגדרה (אין לו מקורות או בורות), הדיברגנץ שלו מתאפס בכל נקודה, כלומר: . לפיכך ניתן לרשום מחדש את המשוואה המרכזית באופן הבא:
אגף ימין של המשוואה החדשה המסומנת ב-(*) הוא מעין גרסה דו-ממדית ולא שלמה של הדיברגנץ של ; הוא מייצג את ההתכנסות או ההתבדרות המקומית של היטלי השדה על מישור xy, בתוך מישור זה. למשוואה האחרונה ניתן לתת כעת פרשנות פיזיקלית: בנקודות התכנסות (או התבדרות) של הזרימה במישור xy, אותם ניתן לתאר בפשטנות כשדה רדיאלי הקורן מתוך נקודת ההתכנסות, תאוצת קוריוליס שואפת להסיט את הזרימה בניצב לכיוון הרדיאלי - כלומר בכיוון המשיקי, ולכן גם היא שואפת להגדיל או להקטין את הערבוליות המקומית במישור xy. במילים אחרות, היכן שיש התכנסות או התבדרות של השדה במישור xy, כוח קוריוליס שואף לשנות את הציקלוניות המקומית.
כאשר הציקלוניות משתנה בשיעור אינפיניטסימלי, גם הספיקה הנפחית לתוך אלמנט הנפח משתנה בשיעור אינפיניטסימלי; מכיוון שאנו מניחים מצב יציב, פירוש הדבר הוא שלאחר פרק זמן dt גם המהירות צריכה להשתנות. לפיכך הדבר תואם למצב של התקדמות גל בכיוון השתנות המופע המרבית (כיוון וקטור הגל ). באופן כללי, שדה המהירויות המקושר לגלים אינרציאליים מזכיר תבריג בורגי; קווי הזרם הרגעיים בנוכחותו של גל אינרציאלי דומים לסליל.







































