פונקציות זוגיות ואי-זוגיות

פונקציות זוגיות ואי-זוגיות הן פונקציות ממשיות בעלות סימטריה מוגדרת ביחס לישר $\ x=0$ (כלומר לציר ה$Y$).

פונקציה זוגית

הגדרה: ערכה זהה עבור כל מספר בתחום ההגדרה ועבור המספר הנגדי לו, כלומר $\ f(x)=f(-x)$.

סימטריה: כל פונקציה זוגית היא סימטרית ביחס לציר ה$Y$.

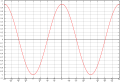
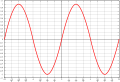
דוגמאות של פונקציות זוגיות:

• 
  $\ f(x)=a$
  פונקציה קבועה
• 
  $\ f(x)=x^{2}$
  פרבולה
• 
  $\ f(x)=\cos(x)$
  קוסינוס
• 
  $\ f(x)=|x|$
  ערך מוחלט

פונקציה אי-זוגית

הגדרה: ערכה עבור כל מספר בתחום ההגדרה הוא המספר הנגדי של ערכה עבור המספר הנגדי לו, כלומר $\ f(-x)=-f(x)$.

סימטריה: כל פונקציה אי-זוגית היא אנטי-סימטרית ביחס לציר ה$Y$ (כלומר יש לה סימטריית סיבוב של $180^{0}$ סביב לראשית).

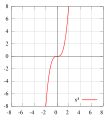
דוגמאות של פונקציות אי-זוגיות:

• 
  $\ f(x)=x$
  פונקציה לינארית
• 
  $\ f(x)=x^{3}$
  פולינום ממעלה שלישית
• 
  $\ f(x)=\sin(x)$
  סינוס
• 
  $\ f(x)=1/x$
  מספר הופכי

פונקציה כללית

הגדרה: פונקציה שאינה פונקציה זוגית ואינה פונקציה אי-זוגית הינה פונקציה כללית כלומר ש- $\ f(x)\neq f(-x)$וגם - $\ f(-x)\neq -f(x)$.

ניתן לייצג כל פונקציה באמצעות סכום של פונקציה זוגית ואי זוגית: $\ f(x)=f_{\text{even}}(x)+f_{\text{odd}}(x)$

וזאת כאשר: $f_{\text{even}}(x)={f(x)+f(-x) \over 2}$ ו $f_{\text{odd}}(x)={f(x)-f(-x) \over 2}$

יצוג זה הוא יחיד. מכאן נובע שמרחב הפונקציות כולן מהווה סכום ישר של מרחבי הפונקציות הזוגיות והאי-זוגיות (כשחיבור וכפל בסקלר מוגדרים נקודתית).

לפעמים, עבור פונקציות מרוכבות, הפונקציה הזוגיות והאי זוגית מיוצגים בהתאמה באופן הבא:
$f_{\text{even}}(x)={f(x)+f^{*}(-x) \over 2}$ ו $f_{\text{odd}}(x)={f(x)-f^{*}(-x) \over 2}$
או:
$f_{\text{even}}(x)=f_{\text{even}}^{*}(-x)$ ו $f_{\text{odd}}(x)=-f_{\text{odd}}^{*}(-x)$

בצורת כתיבה זאת ניתן להוכיח בקלות רבה תכונות של התמרת פורייה.

תכונות

• סכום פונקציות:
  • סכום של פונקציות זוגיות הוא פונקציה זוגית (בפרט, בפתוח של פונקציה אנליטית זוגית לטור טיילור יופיעו רק חזקות זוגיות ובפתוח של פונקציה זוגית מ-$L^{1}$ לטור פורייה יופיעו רק איברי הקוסינוס).
  • סכום של פונקציות אי-זוגיות הוא פונקציה אי-זוגית (בפרט, בפתוח של פונקציה אנליטית אי-זוגית לטור טיילור יופיעו רק חזקות אי-זוגיות ובפתוח של פונקציה אי-זוגית מ-$L^{1}$ לטור פורייה יופיעו רק איברי הסינוס).

• מכפלת פונקציות:
  • מכפלה של פונקציה זוגית בפונקציה זוגית היא פונקציה זוגית.
  • מכפלה של פונקציה אי-זוגית בפונקציה אי-זוגית היא פונקציה זוגית.
  • מכפלה של פונקציה זוגית בפונקציה אי-זוגית היא פונקציה אי-זוגית.
• הרכבת פונקציות:
  • הרכבה של פונקציות זוגיות היא פונקציה זוגית.
  • הרכבה של פונקציות אי-זוגיות היא פונקציה אי-זוגית.
  • הרכבה של כל פונקציה עם פונקציה זוגית היא זוגית (אך לא להפך)
• גזירת פונקציה:
  • נגזרת של פונקציה זוגית היא פונקציה אי-זוגית.
  • נגזרת של פונקציה אי-זוגית היא פונקציה זוגית.
• אינטגרל של פונקציה:
  • כל פונקציה קדומה של פונקציה אי-זוגית היא פונקציה זוגית.
  • לפונקציה זוגית יש פונקציה קדומה אחת שהיא אי-זוגית - הפונקציה שבה המקדם החופשי שווה ל-0. שאר הפונקציות הקדומות הן כלליות.
  • האינטגרל המסוים של פונקציה אי-זוגית בתחום סימטרי שווה לאפס.
  • האינטגרל המסוים של פונקציה זוגית בתחום סימטרי שווה לפעמיים האינטגרל בחצי התחום הסימטרי.
• תכונת האפס: כל פונקציה אי זוגית המוגדרת בנקודה $x=0$ חייבת לקיים $\ f(0)=0$.