סדרת מאייר-ויאטוריס (Mayer–Vietoris sequence) היא סדרה מדויקת המקשרת את חבורות ההומולוגיה של מרחב טופולוגי אל חבורות ההומולוגיה של כיסוי טוב משפט ואן קמפן בחישוב החבורה היסודית .
הסדרה נקראת על שם שני המתמטיקאים האוסטרים לאופולד ויאטוריס ווולטר מאייר , שעסקו רבות בטופולוגיה.
העתקות ההכלה יהי
X
{\displaystyle X}
מרחב טופולוגי . כעת, יהיו
U
,
V
{\displaystyle U,V}
X
{\displaystyle X}
כיסוי טוב פנימים שלהם שווה למרחב:
int
(
U
)
∪
int
(
V
)
=
X
{\displaystyle \operatorname {int} (U)\cup \operatorname {int} (V)=X}
לכל n טבעי נביט בסדרה הבאה[1]
0
⟶
C
n
(
U
∩
V
)
⟶
a
↦
(
i
#
(
a
)
,
−
j
#
(
a
)
)
C
n
(
U
)
⊕
C
n
(
V
)
⟶
(
a
,
b
)
↦
k
#
(
a
)
+
l
#
(
b
)
C
n
(
X
)
⟶
0
{\displaystyle 0\longrightarrow C_{n}(U\cap V){\overset {a\mapsto (i_{\#}(a),-j_{\#}(a))}{\longrightarrow }}C_{n}(U)\oplus C_{n}(V){\overset {(a,b)\mapsto k_{\#}(a)+l_{\#}(b)}{\longrightarrow }}C_{n}(X)\longrightarrow 0}
ממנה מתקבלת סדרה מדויקת של חבורות ההומולוגיה :
⋯
⟶
H
n
(
U
∩
V
)
⟶
H
n
(
U
)
⊕
H
n
(
V
)
⟶
H
n
U
,
V
(
X
)
⟶
H
n
−
1
(
U
∩
V
)
⟶
…
{\displaystyle \dots \longrightarrow H_{n}(U\cap V)\longrightarrow H_{n}(U)\oplus H_{n}(V)\longrightarrow H_{n}^{U,V}(X)\longrightarrow H_{n-1}(U\cap V)\longrightarrow \dots }
כאשר
H
n
{
U
,
V
}
(
X
)
{\displaystyle H_{n}^{\{U,V\}}(X)}
חבורת ההומולוגיה ביחס לכיסוי .
משפט מאייר-ויאטוריס קובע כי העתקת ההכלה
i
:
C
n
{
U
,
V
}
(
X
)
→
C
n
(
X
)
{\displaystyle i:C_{n}^{\{U,V\}}(X)\to C_{n}(X)}
איזומורפיזם טבעי של חבורות
i
∗
:
H
n
{
U
,
V
}
(
X
)
→
H
n
(
X
)
{\displaystyle i_{*}:H_{n}^{\{U,V\}}(X)\to H_{n}(X)}
סדרת מאייר-ויאטוריס :
⋯
⟶
H
n
(
U
∩
V
)
⟶
H
n
(
U
)
⊕
H
n
(
V
)
⟶
H
n
(
X
)
⟶
H
n
−
1
(
U
∩
V
)
⟶
…
{\displaystyle \dots \longrightarrow H_{n}(U\cap V)\longrightarrow H_{n}(U)\oplus H_{n}(V)\longrightarrow H_{n}(X)\longrightarrow H_{n-1}(U\cap V)\longrightarrow \dots }
לרוב נוח להשתמש בסדרת מאייר-ויאטוריס על חבורות ההומולוגיה המצומצמות :
⋯
⟶
H
~
n
(
U
∩
V
)
⟶
H
~
n
(
U
)
⊕
H
~
n
(
V
)
⟶
H
~
n
(
X
)
⟶
H
~
n
−
1
(
U
∩
V
)
⟶
…
{\displaystyle \dots \longrightarrow {\tilde {H}}_{n}(U\cap V)\longrightarrow {\tilde {H}}_{n}(U)\oplus {\tilde {H}}_{n}(V)\longrightarrow {\tilde {H}}_{n}(X)\longrightarrow {\tilde {H}}_{n-1}(U\cap V)\longrightarrow \dots }
האיזומורפיזם
i
∗
:
H
n
{
U
,
V
}
(
X
)
→
H
n
(
X
)
{\displaystyle i_{*}:H_{n}^{\{U,V\}}(X)\to H_{n}(X)}
איזומורפיזם טבעי ביחס להעתקות המכבדות את הכיסוי. כלומר, נניח שנתונים שני מרחבים טופולוגיים בעלי כיסויים טובים
int
(
A
1
)
∪
int
(
B
1
)
=
X
1
{\displaystyle \operatorname {int} (A_{1})\cup \operatorname {int} (B_{1})=X_{1}}
int
(
A
2
)
∪
int
(
B
2
)
=
X
2
{\displaystyle \operatorname {int} (A_{2})\cup \operatorname {int} (B_{2})=X_{2}}
f
:
X
1
→
X
2
{\displaystyle f:X_{1}\to X_{2}}
f
(
A
1
)
⊆
A
2
,
f
(
B
1
)
⊆
B
2
{\displaystyle f(A_{1})\subseteq A_{2},f(B_{1})\subseteq B_{2}}
f
∗
{\displaystyle f_{*}}
דיאגרמה מתחלפת:
בפרט, המעבר מ-
H
n
{
U
,
V
}
(
X
)
{\displaystyle H_{n}^{\{U,V\}}(X)}
H
n
(
X
)
{\displaystyle H_{n}(X)}
לטענה זו מספר שימושים, בעיקר בשילוב עם העובדה שהאיזומורפיזם בין ההומולוגיה הראשונה אל האבליניזציה של החבורה היסודית הוא טבעי - ניתן להבין כך העתקות לא טריוויאליות בסדרת מאייר-ויאטוריס ולחשב את החבורות (ראו בדוגמאות).
כיסוי טוב של הספירה
S
2
{\displaystyle S^{2}}
נוכיח שחבורות ההומולוגיה של הספירות הן
H
~
i
(
S
n
)
=
{
Z
i
=
n
0
i
≠
n
{\displaystyle {\tilde {H}}_{i}(S^{n})={\begin{cases}\mathbb {Z} &i=n\\0&i\neq n\end{cases}}}
נחלק את הספירה לשתי המיספרות עם קצת חיתוך:
B
=
{
x
¯
∈
S
n
:
x
n
<
−
1
10
}
{\displaystyle B=\{{\bar {x}}\in S^{n}:x_{n}<-{\frac {1}{10}}\}}
A
=
{
x
¯
∈
S
n
:
x
n
>
1
10
}
{\displaystyle A=\{{\bar {x}}\in S^{n}:x_{n}>{\frac {1}{10}}\}}
כוויצות , ולכן
H
i
(
A
)
~
=
H
i
(
B
)
~
=
0
{\displaystyle {\tilde {H_{i}(A)}}={\tilde {H_{i}(B)}}=0}
0
→
H
~
i
(
S
n
)
→
H
~
i
−
1
(
S
n
−
1
)
→
0
{\displaystyle 0\to {\tilde {H}}_{i}(S^{n})\to {\tilde {H}}_{i-1}(S^{n-1})\to 0}
כלומר יש איזומורפיזם, ומסיימים באינדוקציה.
נובעות מכך המסקנות הבאות:
השפה של דיסק איננה נסג שלו, אחרת היה מונומורפיזם
Z
=
H
~
n
−
1
(
S
n
−
1
)
↪
H
~
n
−
1
(
D
n
)
=
0
{\displaystyle \mathbb {Z} ={\tilde {H}}_{n-1}(S^{n-1})\hookrightarrow {\tilde {H}}_{n-1}(D^{n})=0}
מקרה פרטי של משפט בורסוק-אולם ).
משפט נקודת השבת של בראוור קובע כי לכל פונקציה רציפה
f
:
D
n
→
D
n
{\displaystyle f:D^{n}\to D^{n}}
נקודת שבת . מוכיחים אותו בשלילה: אחרת, ניתן להגדיר נסיגה
r
:
D
n
→
∂
D
n
{\displaystyle r:D^{n}\to \partial D^{n}}
r
(
x
)
{\displaystyle r(x)}
x
{\displaystyle x}
f
(
x
)
{\displaystyle f(x)}
שיקופים, נקודות שבת ושדות וקטוריים [ עריכת קוד מקור | עריכה ] בסעיף זה נראה טענות מגאומטריה דיפרנציאלית בעזרת הטבעיות של סדרת מאייר-ויאטוריס.
ניישם את הטבעיות למקרה לעיל של הספירות; נוכיח כי השיקוף
R
i
:
S
n
→
S
n
,
n
R
i
(
x
1
…
,
x
n
)
=
(
x
1
,
…
,
−
x
i
,
…
,
x
n
)
{\displaystyle R_{i}:S^{n}\to S^{n},^{n}R_{i}(x_{1}\dots ,x_{n})=(x_{1},\dots ,-x_{i},\dots ,x_{n})}
−
id
{\displaystyle -\operatorname {id} }
n
=
0
{\displaystyle n=0}
A
,
B
{\displaystyle A,B}
i
{\displaystyle i}
כאשר החלק האדום נכון באינדוקציה. לכן:
n
R
i
∗
(
z
)
=
Δ
−
1
(
n
−
1
R
i
∗
(
Δ
(
z
)
)
)
=
Δ
−
1
(
−
Δ
(
z
)
)
=
−
z
{\displaystyle ^{n}R{_{i_{*}}}(z)=\Delta ^{-1}(^{n-1}R{_{i_{*}}}(\Delta (z)))=\Delta ^{-1}(-\Delta (z))=-z}
מהטענה לעיל ניתן להעסיק כי כאשר
n
=
2
k
{\displaystyle n=2k}
A
:
S
n
→
S
n
,
A
(
v
)
=
−
v
{\displaystyle A:S^{n}\to S^{n},A(v)=-v}
הומוטופית לזהות
id
:
S
n
→
S
n
{\displaystyle \operatorname {id} :S^{n}\to S^{n}}
2
k
+
1
{\displaystyle 2k+1}
(
−
1
)
2
k
+
1
id
=
−
id
{\displaystyle (-1)^{2k+1}\operatorname {id} =-\operatorname {id} }
טענה טכנית נוספת היא - אם
f
,
g
:
S
n
→
S
n
{\displaystyle f,g:S^{n}\to S^{n}}
f
(
x
)
≠
g
(
x
)
{\displaystyle f(x)\neq g(x)}
x
∈
S
n
{\displaystyle x\in S^{n}}
f
∼
g
{\displaystyle f\sim g}
H
(
x
,
t
)
=
(
1
−
t
)
f
(
x
)
+
f
g
(
x
)
|
|
(
1
−
t
)
f
(
x
)
+
f
g
(
x
)
|
|
{\displaystyle H(x,t)={\frac {(1-t)f(x)+fg(x)}{||(1-t)f(x)+fg(x)||}}}
מהטענות לעיל ניתן להסיק כי כאשר
n
{\displaystyle n}
f
:
S
n
→
S
n
{\displaystyle f:S^{n}\to S^{n}}
f
(
x
)
=
x
{\displaystyle f(x)=x}
f
(
x
)
=
−
x
{\displaystyle f(x)=-x}
f
≠
id
{\displaystyle f\neq \operatorname {id} }
f
∼
−
id
=
A
{\displaystyle f\sim -\operatorname {id} =A}
f
≠
−
id
{\displaystyle f\neq -\operatorname {id} }
f
∼
id
{\displaystyle f\sim \operatorname {id} }
id
∼
A
{\displaystyle \operatorname {id} \sim A}
מטענה זו ניתן להסיק גם כי כל העתקה רציפה מהמרחב הפרויקטיבי הממשי מממד זוגי
f
:
R
P
n
→
R
P
n
{\displaystyle f:\mathbb {R} P^{n}\to \mathbb {R} P^{n}}
שדה וקטורי של הספירה מממד זוגי חייב להתאפס.
לכל הטענות יש דוגמה נגדית כאשר
n
{\displaystyle n}
n-זר של ספירות הוא איחוד נקודתי שלהן -
S
k
1
∨
⋯
∨
S
k
n
{\displaystyle S^{k_{1}}\vee \dots \vee S^{k_{n}}}
H
~
i
(
S
k
1
∨
…
S
k
t
)
=
Z
∑
j
=
1
n
δ
i
,
k
j
{\displaystyle {\tilde {H}}_{i}(S^{k_{1}}\vee \dots S^{k_{t}})=\mathbb {Z} ^{\sum _{j=1}^{n}{\delta _{i,k_{j}}}}}
כלומר, זו חבורה אבלית חופשית מסדר כמספר הממדים של הספרות ששווה לסדר החבורה.
את הסעיף הקודם ניתן להכליל ולחשב את חבורות ההומולוגיה של כל המשטחים הסגורים : ממיונם ידוע שהם כוללים את הספירות, ה-n-טורוסים וה-n-מישורים פרויקטיביים .
כדי להשתמש בסדרת מאייר-ויאטוריס, ניקח את
U
{\displaystyle U}
n
{\displaystyle n}
V
{\displaystyle V}
משפט ואן קמפן ). אז נקבל
V
≅
∗
,
U
∩
V
≅
S
1
{\displaystyle V\cong *,U\cap V\cong S^{1}}
U
{\displaystyle U}
2
n
{\displaystyle 2n}
⋯
⟶
0
H
~
3
(
U
∩
V
)
⟶
0
H
~
3
(
U
)
⊕
H
~
3
(
V
)
⟶
0
H
~
3
(
X
)
⟶
{\displaystyle \cdots \longrightarrow {\begin{matrix}0\\{\tilde {H}}_{3}(U\cap V)\end{matrix}}\longrightarrow {\begin{matrix}0\\{\tilde {H}}_{3}(U)\oplus {\tilde {H}}_{3}(V)\end{matrix}}\longrightarrow {\begin{matrix}0\\{\tilde {H}}_{3}(X)\end{matrix}}\longrightarrow }
⟶
0
H
~
2
(
U
∩
V
)
⟶
0
H
~
2
(
U
)
⊕
H
~
2
(
V
)
⟶
Z
H
~
2
(
X
)
⟶
{\displaystyle \longrightarrow {\begin{matrix}0\\{\tilde {H}}_{2}(U\cap V)\end{matrix}}\longrightarrow {\begin{matrix}0\\{\tilde {H}}_{2}(U)\oplus {\tilde {H}}_{2}(V)\end{matrix}}\longrightarrow {\begin{matrix}\mathbb {Z} \\{\tilde {H}}_{2}(X)\end{matrix}}\longrightarrow }
⟶
Z
H
~
1
(
U
∩
V
)
⟶
1
→
(
0
¯
,
0
)
Z
2
n
H
~
1
(
U
)
⊕
H
~
1
(
V
)
⟶
Z
2
n
H
~
1
(
X
)
⟶
0
{\displaystyle \longrightarrow {\begin{matrix}\mathbb {Z} \\{\tilde {H}}_{1}(U\cap V)\end{matrix}}{\overset {1\to ({\bar {0}},0)}{\longrightarrow }}{\begin{matrix}{\mathbb {Z} }^{2n}\\{\tilde {H}}_{1}(U)\oplus {\tilde {H}}_{1}(V)\end{matrix}}\longrightarrow {\begin{matrix}{\mathbb {Z} }^{2n}\\{\tilde {H}}_{1}(X)\end{matrix}}\longrightarrow 0}
כאשר את ההעתקה
H
~
1
(
U
∩
V
)
→
H
~
1
(
V
)
{\displaystyle {\tilde {H}}_{1}(U\cap V)\to {\tilde {H}}_{1}(V)}
a
↦
[
a
1
,
b
1
]
⋅
⋯
⋅
[
a
n
,
b
n
]
{\displaystyle a\mapsto [a_{1},b_{1}]\cdot \dots \cdot [a_{n},b_{n}]}
החלוקה לסביבות היא בדיוק כמו ב-
n
{\displaystyle n}
a
→
a
1
2
…
a
n
2
{\displaystyle a\to a_{1}^{2}\dots a_{n}^{2}}
H
~
i
(
n
P
)
=
{
Z
/
2
Z
×
Z
n
−
1
i
=
1
0
i
≠
1
{\displaystyle {\tilde {H}}_{i}(nP)={\begin{cases}\mathbb {Z} /2\mathbb {Z} \times \mathbb {Z} ^{n-1}&i=1\\0&i\neq 1\end{cases}}}
המתיחה של מרחב טופולוגי
X
{\displaystyle X}
S
X
=
(
X
×
I
)
/
{
(
x
1
,
0
)
∼
(
x
2
,
0
)
,
(
x
1
,
1
)
∼
(
x
2
,
1
)
for all
x
1
,
x
2
∈
X
}
{\displaystyle SX=(X\times I)/\{(x_{1},0)\sim (x_{2},0),(x_{1},1)\sim (x_{2},1){\mbox{ for all }}x_{1},x_{2}\in X\}}
H
~
n
(
X
)
=
H
~
n
+
1
(
S
X
)
{\displaystyle {\tilde {H}}_{n}(X)={\tilde {H}}_{n+1}(SX)}
V
=
X
×
[
1
2
,
1
]
/
∼
{\displaystyle V=X\times \left[{\frac {1}{2}},1\right]/\sim }
U
=
X
×
[
0
,
1
2
]
/
∼
{\displaystyle U=X\times \left[0,{\frac {1}{2}}\right]/\sim }
שניהם מרחבים כוויצים , שכן יש נסג עיוותי אל בבסיסים
X
×
{
1
}
{\displaystyle X\times \{1\}}
X
×
{
0
}
{\displaystyle X\times \{0\}}
X
×
{
1
2
}
{\displaystyle X\times \left\{{\frac {1}{2}}\right\}}
X
{\displaystyle X}
0
=
H
~
n
+
1
(
U
)
⊕
H
~
n
+
1
(
V
)
→
H
~
n
+
1
(
S
X
)
→
H
~
n
(
X
)
→
H
~
n
(
U
)
⊕
H
~
n
(
V
)
=
0
{\displaystyle 0={\tilde {H}}_{n+1}(U)\oplus {\tilde {H}}_{n+1}(V)\to {\tilde {H}}_{n+1}(SX)\to {\tilde {H}}_{n}(X)\to {\tilde {H}}_{n}(U)\oplus {\tilde {H}}_{n}(V)=0}
מתקבל איזומורפיזם.
משפט העקומה של ז'ורדן קובע כי עקומה סגורה רציפה במישור מחלקת אותו לשני חלקים, כלומר לשני רכיבי קשירות .
על אף שהוא דיי אינטואיטיבי, אין לו הוכחה פשוטה. אחת ההוכחות הקלות למשפט נתונות בעזרת הומולוגיה: למעשה, בהינתן שיכון
f
:
S
1
→
R
2
{\displaystyle f:S^{1}\to \mathbb {R} ^{2}}
R
2
∖
f
(
S
1
)
{\displaystyle \mathbb {R} ^{2}\setminus f(S^{1})}
Z
2
{\displaystyle \mathbb {Z} ^{2}}
S
1
{\displaystyle S^{1}}
A
{\displaystyle A}
B
{\displaystyle B}
U
=
R
2
∖
f
(
A
)
,
V
=
R
2
∖
f
(
B
)
{\displaystyle U=\mathbb {R} ^{2}\setminus f(A),V=\mathbb {R} ^{2}\setminus f(B)}
סדרת מאייר-ויאטוריס היא כלי חשוב העוזר בפיתוח שיטה כללית ואלגוריתמית לחישוב כל חבורות ההומולוגיה של מרחבי CW סוף-ממדיים מסוימים. יש שימושים חוזרים ונשנים בסדרת מאייר-ויאטוריס בהוכחת השיטה.



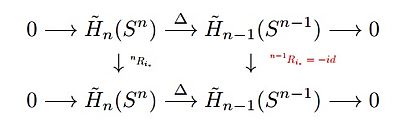

































































![{\displaystyle a\mapsto [a_{1},b_{1}]\cdot \dots \cdot [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fe86318ab4408d19ae3f1f2cbff7257da9fe0e0)




![{\displaystyle V=X\times \left[{\frac {1}{2}},1\right]/\sim }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b26191f6f2ffbf4999f76f62fd62c297a7e7a082)
![{\displaystyle U=X\times \left[0,{\frac {1}{2}}\right]/\sim }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab34dfd9cfaa358359a931b67606f642e161bf23)










