ערבוליות
יש לערוך ערך זה. הסיבה היא: ויקיזציה, חסרות משוואות.
| ||
| יש לערוך ערך זה. הסיבה היא: ויקיזציה, חסרות משוואות. | |
במכניקת הרצף, ובהידרודינמיקה בפרט, הערבוליות (באנגלית: vorticity) היא גודל וקטורי המודד את מידת הסחרור המקומית של תווך חומרי בנקודה מסוימת (נטייתו של עצם המוצב באותה נקודה להסתובב סביב עצמו), כפי שהייתה מורגשת על ידי צופה המוצב באותה נקודה ונודד ביחד עם הזרימה. זהו גודל חשוב בתאוריה הדינמית של זורמים המספק מסגרת מושגית נוחה להבנת מגוון תופעות מורכבות הקשורות בזורמים, כמו למשל היווצרותן ותנועתן של טבעות מערבולות.
מתמטית, הערבוליות מוגדרת כרוטור של שדה המהירות :
כאשר היא אופרטור דל. קונספטואלית, ניתנת להמחשה באמצעות "סימון" חלקים של הזורם בסביבה קטנה של הנקודה הנחקרת, וצפייה בשינויי המיקום היחסי שלהם כאשר הם נעים ביחד עם הזרימה. הערבוליות תהיה אז פעמיים וקטור המהירות הזוויתית של חלקיקי הנוזל בתוך הסביבה ביחס למרכז המסה שלהם, ועם כיוון הנקבע בהתאם לכלל יד ימין.
רקע[עריכת קוד מקור | עריכה]
בדינמיקה של זורמים מערבולת (Vortex) מוגדרת כאזור בזורם שמתבצעת בו רוטציה (תנועה סיבובית) ביחס לעקום מסוים היכול להיות ישר או מעוגל ונקרא ציר המערבולת. ניתן לצפות ולהבחין במערבולות במקרים רבים בחיי היום יום כגון: סופת טורנדו, מערבולות שנוצרות בים מתנועת סירות, מערבולות קצה כנף וכו'.
מערבולות מהוות רכיב מרכזי בזרימה טורבולנטית והן קיימות לרוב בזרימה זו יותר מאשר בזרימה למינרית. התפלגות שדה המהירות, וקטור הערבוליות וכמו כן עקרונות של סירקולציה משמשים כיום לאפיון של מערבולות ושל תופעת הערבוליות. במרבית המערבולות מהירות הזרימה היא מקסימלית בסמוך לציר המערבולת שביחס אליו מתבצעת הרוטציה והיא קטנה ביחס הפוך למרחק מציר זה, אולם קיימות גם מערבולות שבהן המהירות גדלה ביחס ישר למרחק מציר המערבולת.
כאשר נוצרות מערבולות הן יכולות לנוע, לגדול, להתפתל וליצור אינטראקציות שונות עם מערבולות נוספות, מערבולת שנעה נושאת עמה מסה, אנרגיה ותנע.
דוגמאות[עריכת קוד מקור | עריכה]
במסה של תווך חומרי רציף הסובב כגוף קשיח, הערבוליות היא פעמיים וקטור המהירות הזוויתית של הסיבוב הזה. זהו המצב, למשל, בליבה המרכזית של מערבולת רנקין.
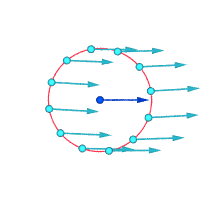
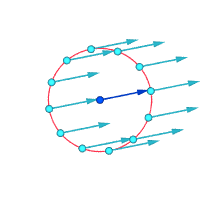
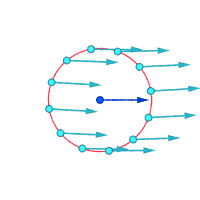
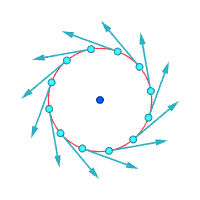
הערבוליות עשויה להיות שונה מאפס אפילו כאשר כל חלקיקי הזורם נעים לאורך קווי מסלול ישרים ומקבילים, אם קיימת גזירה (במילים אחרות, אם מהירות הזרימה משתנה כאשר נעים בניצב לקווי הזרם). לדוגמה, בזרימה למינרית בתוך צינור עם חתך רוחב קבוע, כל החלקיקים נעים במקביל לציר הצינור; אולם מהר יותר ליד הציר, ולאט מאוד (למעשה במהירות אפסית לפי כל אמת מידה) בסמוך לדפנות הצינור. הערבוליות תהיה אפס על הציר, ובעלת ערך מרבי בסמוך לדפנות, שם אפקט הגזירה הוא מרבי.
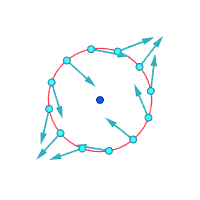
בכיוון ההפוך, לזרימה עשויה להיות ערבוליות אפס גם כאשר כל החלקיקים נעים לאורך מסלולים עקומים. דוגמה לכך היא המערבולת האי-רוטציונית האידיאלית, שבה רוב החלקיקים מסתובבים סביב לציר ישר מסוים, עם מהירויות העומדות ביחס הפוך למרחק החלקיק מהציר הזה. אלמנט קטן של הרצף שאינו חותך את ציר הסיבוב יסתובב בכיוון אחד אך יחווה גזירה בעוצמה זהה בכיוון ההפוך, באופן כזה שהמהירות הזוויתית הממוצעת של החלקיקים המרכיבים את האלמנט ביחס למרכז המסה שלהם היא בדיוק אפס.
דרך אחרת לדמיין ערבוליות היא להניח שרגעית, חלק זעיר של הרצף הופך למוצק בעוד שאר הזורם נעלם לפתע. אם החלקיק המוצק הקטן הזה מסתובב, במקום פשוט לנוע בתנועת העתקה קווית בלבד, אז ישנה ערבוליות בזורם. באיור למטה, תת-התמונה השמאלית מדגימה מצב של אפס ערבוליות, ותת התמונה הימנית מדגימה מצב בו קיימת ערבוליות.
הגדרה מתמטית[עריכת קוד מקור | עריכה]
מתמטית, הערבוליות של שדה זרימה תלת-ממדי היא פסאודווקטור, שבדרך כלל מסומן , המוגדר כרוטור של שדה המהירות המתאר את תנועת הזורם. בקואורדינטות קרטזיות:
באופן מילולי, הערבוליות מתארת כיצד וקטור המהירות משתנה כאשר נעים מרחק אינפיניטסימלי בכיוון ניצב אליו.
בזרימה דו־ממדית בה המהירות אינה תלויה בקואורדינטה ואין לה רכיב בכיוון , וקטור הערבוליות תמיד מצביע בכיוון ציר , כך שהוא יכול להיות מתואר כשדה סקלרי המוכפל בוקטור יחידה :
הערבוליות קשורה לסירקולציה (אינטגרל קווי של המהירות) לאורך מסלול סגור דרך משפט סטוקס. ביותר פירוט, בעבור כל אלמנט שטח אינפיניטסימלי C עם וקטור יחידה נורמלי ושטח , הסירקולציה לאורך ההיקף של היא המכפלה הסקלרית כאשר היא הערבוליות במרכז C.
דוגמאות ליישום ההגדרה[עריכת קוד מקור | עריכה]
נבחן את ההגדרה הזאת עבור שניים מהמקרים שתוארו מקודם (מערבולת קשיחה ומערבולת אי-רוטציונית). לשם כך נעזר בהגדרת אופרטור דל בקואורדינטות גליליות:
- מערבולת קשיחה: במקרה זה מתקיים , והצבה בביטוי לאופרטור דל בקואורדינטות גליליות מגלה שהסירקולציה מפולגת באופן אחיד בתוך חתך רוחב של המערבולת, עם ערבוליות ששווה בכל נקודה לפעמיים המהירות הזוויתית של סחרור המערבולת.
- מערבולת אי-רוטציונית: במקרה זה מתקיים , והצבה מגלה שהסירקולציה מפולגת באופן אחיד כשלמעשה הערבוליות (שהיא גם הצפיפות המשטחית של הסירקולציה) מתאפסת בכל נקודה פרט לראשית; בראשית ישנה נקודת סינגולריות של הערבוליות. מתמטית הערבוליות היא פונקציית דלתא של דיראק, כך שהסירקולציה הכוללת בכל מעגל סביב הראשית קבועה בערכה.
שימושים בתחומי מדע מסוימים[עריכת קוד מקור | עריכה]
אווירונאוטיקה[עריכת קוד מקור | עריכה]
באווירודינמיקה, פילוג העילוי על פני כנף סופית ניתן לקירוב תחת ההנחה שלכל קטע של הכנף ישנה מערבולת זנב חצי אינסופית מאחוריו. לאחר מכן ניתן למצוא את חוזק המערבולות הללו בעזרת ההנחה שאין אף זרימה דרך משטח הכנף. תהליך זה נקרא שיטת לוח הערבוליות של מכניקת הזורמים החישובית. חוזק המערבולות נסכם לאחר מכן כדי למצוא את הסירקולציה הכוללת מסביב לכנף. לפי משפט קוטה-ז'וקובסקי, העילוי הכולל יחסי למכפלת הסירקולציה, מהירות האוויר, וצפיפות האוויר.
מדעי האטמוספירה[עריכת קוד מקור | עריכה]
הערבוליות היחסית היא הערבוליות יחסית לכדור הארץ (כלומר יחסית לנקודה קבועה על הקרקע) של שדה מהירות האוויר. שדה מהירות האוויר ממודל לעיתים קרובות כזרימה דו-ממדית המקבילה לקרקע, כך שוקטור הערבוליות הוא גודל סיבובי סקלרי הניצב לקרקע. הערבוליות חיובית כאשר - כשמסתכלים מנקודת המבט של צופה על פני הקרקע - הרוח מסתחררת כנגד כיוון השעון. בחצי הכדור הצפוני, ערבוליות חיובית נקראת סיבוב ציקלוני, וערבוליות שלילית נקראת סיבו אנטי-ציקלוני; המינוח המקובל מתהפך עבור חצי הכדור הדרומי.
הערבוליות המוחלטת מחושבת דרך מהירות האוויר ביחס למערכת ייחוס אינרציאלית. היא שווה לסכום הערבוליות היחסית ואיבר ערבוליות נוסף הנקרא ערבוליות פלנטרית; האיבר האחרון למעשה מכמת את מידת הסיבוב העצמי של גושי אוויר אודות לסיבוב כדור הארץ, והוא שווה לפרמטר קוריוליס המקומי.
הערבוליות הפוטנציאלית (נקראת גם ערבוליות מוכללת) היא הערבוליות המוחלטת המחולקת במרווח האנכי בין מפלסים שווי טמפרטורה פוטנציאלית. הערבוליות המוחלטת של מסת אוויר תשתנה אם גוש האוויר נמתח (או נדחס) בכיוון האנכי, אולם היא נשמרת בזרימה אדיאבטית. כיוון שזרימה אדיאבטית היא הדומיננטית ביותר באטמוספירה, הערבוליות הפוטנציאלית משמשת כאמצעי סימון של גושי אוויר באטמוספירה בקנה מידה זמני של ימים אחדים.
משוואת הערבוליות הברוטרופית היא האמצעי החישובי הפשוט ביותר המשמש כדי לחזות את תנועתם של גלי רוסבי (את נקודות השיא והשפל של מפלס הלחץ של 50,000 פסקל) בפרק זמן מוגבל (ימים אחדים). בשנות ה-50, התוכנות המוצלחות הראשונות לחיזוי נומרי של מזג האוויר עשו שימוש ישיר במשוואה הזאת.
קשור באופן ישיר למושג הערבוליות הוא מושג הבורגיות (helicity) של שדה וקטורי, המוגדר כ-
כאשר האינטגרל נלקח על פני נפח נתון . המכפלה הפנימית מודדת עד כמה פרודות הזורם בנקודה מסוימת נעות במקביל לציר הערבול, תוך כדי שהן מסתחררות סביבו (מכפלה זו מכמתת מקומית את כמות הבורגיות ליחידת נפח). במדעי האטמוספירה, מידת הבורגיות של תנועת אוויר באזור מסוים היא חשובה לצורך חיזוי היווצרותם של תאי-על והערכת הפוטנציאל לפעילות טורנדית.











![{\displaystyle {\begin{aligned}{\vec {\omega }}=\nabla \times {\vec {v}}&={\begin{pmatrix}{\dfrac {\partial }{\partial x}}&\,{\dfrac {\partial }{\partial y}}&\,{\dfrac {\partial }{\partial z}}\end{pmatrix}}\times {\begin{pmatrix}v_{x}&v_{y}&v_{z}\end{pmatrix}}\\[6px]&={\begin{pmatrix}{\dfrac {\partial v_{z}}{\partial y}}-{\dfrac {\partial v_{y}}{\partial z}}&\quad {\dfrac {\partial v_{x}}{\partial z}}-{\dfrac {\partial v_{z}}{\partial x}}&\quad {\dfrac {\partial v_{y}}{\partial x}}-{\dfrac {\partial v_{x}}{\partial y}}\end{pmatrix}}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31ecb1ab8f776eae0702f8a1dda301fa72827def)


![{\displaystyle {\begin{aligned}{\vec {\omega }}=\nabla \times {\vec {v}}&={\begin{pmatrix}{\dfrac {\partial }{\partial x}}&\,{\dfrac {\partial }{\partial y}}&\,{\dfrac {\partial }{\partial z}}\end{pmatrix}}\times {\begin{pmatrix}v_{x}&v_{y}&v_{z}\end{pmatrix}}\\[6px]&=\left({\frac {\partial v_{y}}{\partial x}}-{\frac {\partial v_{x}}{\partial y}}\right){\hat {z}}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82ebcb73cdb66d1532f0abb182af5bfcebf88021)











