0.999...
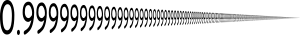
במתמטיקה, הסימון 0.999... מציין את הפיתוח העשרוני האינסופי, שבו כל הספרות שאחרי הנקודה העשרונית הן 9. על-פי ההגדרה המקובלת לפיתוח העשרוני, המספר שווה ל־1. השוויון 0.999…=1 אינו ייחודי; כל מספר ממשי בעל שבר עשרוני סופי אפשר לייצג גם באמצעות שבר עשרוני המסתיים בסדרה אינסופית של תשיעיות. כך למשל, המספר 13.412 ניתן לייצוג גם בתור המספר 13.411999…. תכונה זו בעצמה אינה ייחודית לכתיב העשרוני: לכל בסיס b, אפשר לייצג כל שבר סופי גם בעזרת רצף אינסופי שבו חוזרת הספרה b-1.
אף על פי שהשוויון מקובל ללא עוררין על הקהילה המדעית, הגדרת הפיתוח העשרוני מסתמכת על המושג "טור מתכנס" מתחום האנליזה המתמטית. ישנם אנשים שאינם מכירים, אינם מבינים או אינם מקבלים רעיונות אלה, מתנגדים לשוויון ומנסים ליצור גישות אלטרנטיביות בהן הוא לא יתקיים. קיימות מערכות מספרים ושיטות כתיבה אחרות בהן לביטוי 0.999… אין משמעות או יש משמעות שונה מ-1, אולם בכל דרך עקבית להציג את המספרים הממשיים באמצעות שברים עשרוניים שוויון זה יתקיים.
העוסקים בחינוך מתמטי מכירים את הקושי שבקבלת השוויון של המספר שבכותרת ל-1. גם בקבוצת הדיון sci.math[1], נערכו דיונים רבים בנושא השוויון, ואלו הביאו בסופו של דבר להכללת הסברים עבורו בקובץ השאלות והתשובות של הקבוצה.
קיימת הוכחה פשוטה לשוויון 0.999... = 1, המבוססת על ההנחות הבאות:
- לשבר עשרוני אינסופי יש ערך מוגדר היטב ויחיד.
- כפל של שבר עשרוני אינסופי בעשר שווה לשבר המתקבל מהזזת הנקודה העשרונית מקום אחד ימינה.
- אפשר לחסר שברים עשרוניים אינסופיים.
שלבי ההוכחה הם:
| יהי | |
| לכן, | |
| ניתן לחסר מ־ את ומתקבל: | |
| כלומר, | |
| כלומר, | |
| ולפיכך: |
מבחינה מתמטית אין עניין מיוחד בשוויון 0.999... = 1. הוא מסקנה מיידית מהגדרת הפיתוח העשרוני של מספר ממשי. אולם השוויון מושך תשומת לב רבה בהוראת המתמטיקה כיוון שהוא מקרה מבחן להבנת מושגים רבים, וביניהם: מספר ממשי, טור, סדרה, גבול, פיתוח עשרוני אינסופי ועוד. אמנם מושגים אלה יסודיים מאוד במתמטיקה המודרנית, אך הם עמוקים וקשים להבנה. בהתאם, בבית הספר הם נלמדים באופן שטחי בלבד, ולמידה מעמיקה שלהם מתבצעת רק במסגרת לימודים אקדמיים במתמטיקה.
פיתוח עשרוני[עריכת קוד מקור | עריכה]
 ערך מורחב – השיטה העשרונית
ערך מורחב – השיטה העשרונית
בשיטה העשרונית, שבה אנו משתמשים בחיי היום-יום והיא גם שיטת הספירה המקובלת במתמטיקה, מבטאים כל מספר שלם כסכום של חזקות של 10, המוכפלות בספרות 0 עד 9. בשיטה העשרונית אפשר להציג כשבר עשרוני סופי רק את המספרים השווים למנת החילוק של מספר טבעי a בחזקה שלמה של 10, . מספרים רבים, ובהם מספרים רציונליים רבים, כגון , לא ניתן להציג באופן זה (משום ש-3 אינו מחלק אף חזקה של 10). מתברר, שכל מספר רציונלי, ואף כל מספר ממשי x, אפשר להציג כסכום אינסופי של חזקות (שליליות) של 10, הנקרא "הפיתוח העשרוני" של x; אבל עובדה זו אינה מובנת מאליה, ואף אינה דרושה כאן.
פיתוח עשרוני אינסופי[עריכת קוד מקור | עריכה]
בדיוק כפי שרצף ספרות סופי מובן כסכום , שהוא לעולם מספר רציונלי, אפשר להבין את הרצף האינסופי כסכום אינסופי, . סכום כזה נקרא "טור עשרוני", המתאים לשבר העשרוני האינסופי .
בגישה זו (שהיא התפיסה המקובלת במתמטיקה, ללא עוררין), יש שתי בעיות.
- ראשית, מהי המשמעות של סכום אינסופי? מרגע שהוגדר הסכום של שני מספרים, אפשר להגדיר את הסכום של כל קבוצה סופית של מספרים באינדוקציה; אולם, הגדרה זו אינה מעניקה מובן לסכום של קבוצה אינסופית, ומושג זה דורש הגדרה חדשה. במהלך הטיפול במושג החדש מתברר עד מהרה שקל יותר לטפל בסכום של קבוצה שאיבריה ממוספרים על ידי מספרים טבעיים (1,2,3,…), במקום בסכום של קבוצה כללית. קבוצות כאלה נקראות סדרות. לסדרה שאותה מבקשים לסכם, קוראים במתמטיקה טור; בסוגיית הסיכום של טורים עוסק החשבון האינפיניטסימלי (ראו גם גבול של סדרה). בכל הגדרה מקובלת לסכום של טור, יש טורים שקיים להם סכום (אלו נקראים "טורים מתכנסים"), וטורים שלא קיים להם סכום (אלו נקראים "טורים מתבדרים"). כל הטורים העשרוניים מתכנסים.
- כאן מתעוררת הבעיה השנייה - היכן מחשבים את הסכום? כל טור עשרוני מתכנס למספר ממשי, אבל מספרים אלה בדרך-כלל אינם רציונליים. במילים אחרות, יש טורים עשרוניים שאינם מתכנסים למספר רציונלי. עובדה זו ניתן לבטא בשתי דרכים: מנקודת המבט של המספרים הרציונליים, לטור כזה אין סכום; ומנקודת המבט של המספרים הממשיים, יש לו סכום, שאינו רציונלי.
לכן כדי לתת משמעות לשבר עשרוני יש לקבוע תחילה איזה סוג מספר הוא מתאר ובאיזה מושג של התכנסות משתמשים כדי לפרש אותו. בהקשרים מסוימים יש יותר ממשמעות אחת למושג ההתכנסות. קביעת משמעות למושג ההתכנסות נעשית בדרך כלל על ידי קביעת טופולוגיה. מקובל לתאר באמצעות שברים עשרוניים אינסופיים מספרים ממשיים. על אוסף המספרים הממשיים יש טופולוגיה מקובלת אחת, לפי טופולוגיה זאת סכום של טור חיובי הוא המספר הקטן ביותר אשר גדול מכל הסכומים הסופיים של איברי הטור.
יש דרך קלה להבחין בין הטורים העשרוניים שסכומם רציונלי, לאלו שסכומם אינו כזה. בשבר עשרוני מחזורי יש קבוצת ספרות החוזרת שוב ושוב ממקום מסוים והלאה. בשבר כזה מקובל לסמן את הקבוצה החוזרת בקו עילי או בנקודות עיליות, או להמשיך את השבר בשלוש נקודות, כאשר הקבוצה החוזרת מובנת מן ההקשר. כך למשל מסמן את השבר שבו, לאחר הספרה 5, באות הספרות 90 שוב ושוב. באופן דומה, בפיתוח העשרוני , שלוש הנקודות מציינות שהפיתוח אינו מסתיים, והספרה 3 מופיעה בו בכל מקום משם והלאה. מספר זה שונה, מן השבר הסופי 0.333. מתברר שלכל טור עשרוני מחזורי יש סכום רציונלי, ולכל טור עשרוני שאינו מחזורי יש סכום שאינו רציונלי.
סיכום של שברים עשרוניים[עריכת קוד מקור | עריכה]
כדי להעניק משמעות לכל שבר עשרוני (מחזורי או שאינו מחזורי) יש להקדים ולפתח באופן מסודר את שדה המספרים הממשיים (באחת משתי השיטות המקובלות, סדרות קושי או חתכי דדקינד, או בדרך אחרת). לאחר מכן, ההגדרה המקובלת, והמתבקשת מאליה, תתאים לביטוי הפורמלי את המספר הממשי היחיד שהוא סכומו של הטור . בגישה זו יש להוכיח שהטור מתכנס (במרחב של המספרים הממשיים).
אף-על-פי-כן, אם מעוניינים לסכם רק שברים עשרוניים מחזוריים (כגון השבר 0.999…), אין בכך צורך: סכומו של הטור ההנדסי הוא , ולכן אפשר לקבל, כהגדרה, שהשבר המחזורי מסתכם למספר הרציונלי [2] לחלופין, אפשר להוכיח את נכונותה של נוסחה זו, אם מניחים שתי הנחות:
- הביטוי (המחזורי) מייצג מספר בשדה כלשהו.
- ביטויים מסוג זה מקיימים את החוק .
משתי הנחות אלה נובע, למשל, כי , ולכן .
0.999… בהגדרות שונות של שדה המספרים הממשיים[עריכת קוד מקור | עריכה]
יש מספר דרכים שקולות להגדיר את המושג של מספר ממשי.
מספרים ממשיים בתור מחלקות שקילות של ביטויים עשרוניים[עריכת קוד מקור | עריכה]
אחת הדרכים האלמנטריות לעשות זאת היא להגדיר מספר ממשי בתור ביטוי עשרוני (זאת אומרת רצף מהצורה כאשר ו- הם ספרות) עד כדי יחס השקילות הבא:
בגישה זאת השוויון נובע ישירות מההגדרה, מכיוון שעל-פי יחס השקילות שהוגדר מעלה שני ייצוגים אלה שקולים. לזכותה של הגדרה זאת ניתן לומר שהיא מפורשת ואלמנטרית. עם זאת, הקשר בינה לבין ההגדרה המקובלת למספרים ממשיים אינו מובן מאליו, וקשה גם להגדיר את פעולות החשבון הבסיסיות מתוך הגדרה זאת.
גישה אקסיומטית למספרים ממשיים[עריכת קוד מקור | עריכה]
במקום להגדיר את אוסף המספרים הממשיים מתוך "הוראות הרכבה", ניתן להגדיר אותם באמצעות רשימת תכונות שנדרשות מהם. תכונות אלה נקראות אקסיומות, ויש מספר מערכות של אקסיומות המתארות את המספרים הממשיים ביחידות עד כדי איזומורפיזם. זאת אומרת שלא יכולות להיות שתי דוגמאות שונות לקבוצות עם פעולות שיקיימו את מערכת האקסיומות. אלא אם דוגמאות אלה יהיו שקולות במובן שתהיה העתקה חח"ע ועל בין הקבוצות ששומרת על הפעולות.
אחת ממערכות האקסיומות המגדירות את המספרים הממשיים היא מערכת האקסיומות של שדה סדור שלם. בשדה סדור שלם הגבול של סדרה עולה שווה לסופרמום שלה. זאת אומרת למספר הקטן ביותר שגדול או שווה לכל איברי הסדרה. על פי גישה זאת, על מנת להוכיח את השוויון יש להסיק אותו מהאקסיומות. להלן דוגמה להוכחה כזאת:
- נסמן כאשר הספרה 9 חוזרת על עצמה פעמים.
- תחילה מוכיחים באינדוקציה ש
- לכן הסדרה עולה וחסומה מלעיל.
- לכן, לפי אקסיומת השלמות, לסדרה יש גבול
- לפי ההגדרה גבול זה הוא הערך של השבר העשרוני .
- כעת קל להסיק ש כפי שהוסבר מעלה.
היתרון הגדול של הגישה האקסיומטית היא האוניברסליות שלה. כל בנייה של המספרים הממשיים תקיים את האקסיומות וכל קבוצה עם פעולות שמקיימת את האקסיומות יכולה להיקרא קבוצת המספרים הממשיים. כמו כן האקסיומות עצמן אינטואיטיביות למדי, ומתיישבות עם הניסיון היום יומי שלנו עם מושג המספרים הממשיים. מה שלא ברור אינטואיטיבית הוא שהאקסיומות מספיקות כדי לתאר את המספרים הממשיים, ושכל עובדה שנכונה עבור המספרים הממשיים תהיה נכונה עבור כל קבוצה המקיימת את האקסיומות. טענה זאת נובעת מהיחידות (עד כדי איזומורפיזם) של קבוצת המספרים הממשיים. יחידות זאת קל יחסית להוכיח פורמלית (בהסתמך על האקסיומות של תורת הקבוצות).
החיסרון של הגישה האקסיומתית הוא שהגישה לא מספקת בנייה מפורשת לקבוצת המספרים הממשיים. היא לא נותנת באופן ישיר את התשובה לשאלה "מהוא מספר ממשי?". כמו כן היא לא מוכיחה שקימת קבוצה המקיימת את כל האקסיומות. לכן כדאי להשלים גישה זאת על ידי בנייה מפורשת של המספרים הממשיים והוכחה שהאקסיומת מתקיימות עבור בנייה זאת. בנייה מפורשת כזאת תספק גם הוכחה שמערכת האקסיומות של המספרים הממשיים היא עקבית, בהינתן העקביות של תורת הקבוצות.
ניתן להוכיח שהבנייה שמופיעה מעלה מקיימת את האקסיומות, אולם ההוכחה מסורבלת, לכן בדרך כלל מעדיפים בניות אחרות.
בניות נוספות של המספרים ממשיים[עריכת קוד מקור | עריכה]
שתי הבניות המקובלות לשדה המספרים הממשיים הן חתכי דדקינד ומחלקות שקילות של סדרות קושי. שתי הבניות מתבססות על אותו רעיון כללי:
- תחילה מניחים שהמושג "מספר ממשי" כבר קיים.
- לאחר מכן מוצאים דרך לתאר ביחידות מספר ממשי על ידי מספרים רציונליים. במילים אחרות למצוא לו מעין תעודת זהות המורכבת ממספרים רציונליים. במקרה של חתכי דדקינד, "תעודת הזהות" היא קבוצת המספרים הרציונליים הקטנים מ - . במקרה של סדרות קושי "תעודת הזהות" היא קבוצת הסדורת של מספרים הרציונליים המתכנסות ל - .
- לבסוף מאפינם מה יכול להוות תעודת זהות של מספר ממשי (לפי הגישה שניבחרה) ואז מגדירים מספר ממשי להיות "תעודת הזהות" שלו.
רעיון זה עלול להראות קונטרא-אינטואיטיבי כי נדמה שמה שאנחנו מגדירים זה לא המספר עצמו אלה משהוא שמיצג אותו. למעשה רעיון זה שימושי מאוד בכל המתמטיקה, כיוון שבמתמטיקה בדרך כלל אין משמעות למהות האובייקטים עצמם אלה רק לאוסף האובייקטים הרלוונטיים והאינטראקציות ביניהם. כך אפשר לראות, הן חתך דדקינד והן במחלקת שקילות של סדרות קושי בתור שמות שונים לאותו מספר ממשי.
כדי להוכיח את השוויון (או כל טענה אחרת) בבנייה מפורשת מסוימת, די להוכיח שהאקסיומות של המספרים הממשיים מתקיימות בבנייה זאת. העובדה שהשוויון נובע מהאקסיומות הוסברה לעליל. ניתן גם להסיק שוויון זה ישירות מכל אחת מהבניות האלה.
קשיים שמעלה הביטוי ...0.999 בהוראת המתמטיקה[עריכת קוד מקור | עריכה]
השוויון מעלה מספר קשיים אצל תלמידים רבים:
- המושג מספר ממשי, ובהתאם לכך המושגים גבול ופיתוח עשרוני אינסופי, הם מושגים מסובכים. לראיה, אף על פי שבאופן אינטואיטיבי המושג מוכר לאנושות כבר אלפי שנים, הגדרה פורמלית שלו הופיעה רק במאה ה-19.
- האגף השמאלי של השוויון הוא ביטוי אינסופי. שום "קטימה" (clipping), כלומר ביטוי סופי שלו, לא שווה בדיוק ל-1. למעשה, גם הסדרה שמתקבלת מהקטימות השונות שלו איננה המספר 1, אלא רק סידרה (אחת מני רבות) שמתכנסת למספר 1. המוסכמה ששבר עשרוני אינסופי מייצג את הגבול של הסדרה שמתקבלת מהקטימות השונות שלו - מסובכת להבנה.
- בעוד שהביטוי באגף שמאל מסובך מאוד, הביטוי באגף ימין פשוט ביותר.
- השוויון מהווה שתי דרכים שונות לכתוב את אותו המספר. בפני עצמו הדבר לא אמור להעלות קושי. גם השוויון הוא כזה. אולם איננה דרך "תיקנית" לכתוב את , אלא ביטוי חשבוני שנותן את . דוגמאות דומות יותר הן השוויונים: ו- , שגם הם מעלים קשיים מסוימים (אם כי קטנים בהרבה). אחד הדברים שמקל על ההבנה של השוויון הוא העובדה שלסימן השבר, מלבד היותו חלק מהסימון של מספרים רציונליים, יש גם משמעות של חילוק, לכן אפשר להבין גם אותו כתוצאה של פעולת חילוק, ולא רק כשתי דרכים שונות לכתוב את 1 כשבר. כמובן, שאר הקשיים שצוינו מעלה אינם קיימים בעבור השוויון . הסיטואציה עם דומה.
קשיים אלה מושכים תשומת לב רבה לנושא.[3], ולא פעם ניסו אנשים להגדיר את המספרים הממשיים באופן שבו השוויון לא יתקיים. בנוסף לעובדה שהגדרות אלה נוטות להיות בלתי-עקביות ולא מנוסחות היטב, הרי שהן נידונו לכישלון – אלא אם כן מוכנים לוותר על חלק מהתכונות הבסיסיות של המספרים הממשים ושל הפיתוח העשרוני שלהם.
עם זאת, כמו כל טענה מתמטית, שוויון זה תלוי בהגדרות שלפיהן מפרשים את שני אגפי השוויון. לדוגמה, אם מפרשים את אגף שמאל כפיתוח בבסיס גדול מ-10, אז השוויון לא נכון. גם אם מפרשים את שני האגפים כביטויים עשרוניים ולא כערכים המספריים שלהם, אז הם כמובן שונים.
תופעת היצוג כפול על ידי שבר עשרוני במתמטיקה[עריכת קוד מקור | עריכה]
אוסף הביטויים העשרוניים[עריכת קוד מקור | עריכה]
אם נסמן ב- את אוסף כל הביטויים מהצורה כך ש- ו- הם ספרות עשרוניות לכל , אז ניתן להתייחס לייצוג עשרוני של מספר בתור העתקה . העובדה שלמספרים ממשיים מסוימים יש יותר מייצוג עשרוני אחד אומרת שההעתקה הזאת איננה חד-חד ערכית. העובדה שלכל מספר ממשי יש ייצוג עשרוני אומרת שהעתקה זאת היא על. לא ניתן להגדיר מבנה של שדה על שיתאים למבנה השדה על . אולם ניתן להגדיר טופולוגיה על שתתאים לטופולוגיה על . זאת אומרת להגדיר על טופולוגיה כך ש תהיה פונקציה רציפה ופונקציה פתוחה. במילים אחרות הטופולוגיה על תתקבל כטופולוגיית מנה של . כך שכל מה "שחסר" כדי ש תהיה הומיאומורפיזם זה ש תהיה חד-חד ערכית. מאידך, הטופולוגייות על ועל מאוד שונות. למשל, בעוד ש- מרחב קשיר, הרי ש- אינו קשיר לחלוטין.
אם מתמקדים בקטע הסגור אז העתקה הופכת להיות כאשר הטופולוגיה על היא טופולוגיית המכפלה. המרחב הומיאומורפי לקבוצת קנטור.
ניתן להחליף את בסיס הספירה בכל בסיס ספירה אחר והתוצאה תהיה דומה.
תופעת היצוג הכפול בחישוב עוצמת הממשיים[עריכת קוד מקור | עריכה]
לתופעת היצוג הכפול על ידי שבר עשרוני יש השפעה (מינורית) על הוכחת העובדה שעוצמת שדה המספרים הממשיים היא . ההוכחה הסטנדרטית של עובדה זאת מתבססת על ההעתקה שהוגדרה מעלה. קל לראות ש היא מעוצמה (למעשה זה פשוט עוד יותר כשעובדים בבסיס 2) אך מכיוון ש- איננה חד-חד ערכית זה לא אומר באופן מיידי שזו גם עוצמת שדה הממשיים. קל להסיק זאת באמצעות משפט קנטור-ברנשטיין אך למעשה גם לא קשה להוכיח זאת ישירות במקרה זה.
מספרים p-אדיים[עריכת קוד מקור | עריכה]
 ערך מורחב – מספר p-אדי
ערך מורחב – מספר p-אדי
המספרים ה-p-אדיים מהווים מערכת מספרים מקבילה למספרים הממשיים. המספרים ה-p-אדיים שונים מאוד בתכונותיהם מהמספרים הממשיים אך באספקטים מסוימים הם אנלוגיים למספרים הממשיים. מספרים p-אדיים ניתן לכתוב כשברים על פי בסיס ספירה ראשוני p. גם שברים אלה אינסופיים אבל באופן שונה: יש להם מספר סופי של ספרות לאחר הנקודה ומספר אינסופי של ספרות לפניה. הסיבה לכך שהמספר p קטן מ-1 בתור מספר p-אדי. הבדל זה גורם לכך שהמספרים ה-p-אדיים מתנהגים מאוד שונה מהמספרים הממשיים הן מבחינה אריתמטית והן מבחינה טופולוגית. תופעת היצוג הכפול לא קיימת בספרים ה-p-אדיים: לכל מספר p-אדי יצוג יחיד על ידי שבר בבסיס ספירה p. זה למעשה ההבדל הטופולוגי בין המספרים ה-p-אדיים לממשיים. הדבר גורם לכך ששדה המספרים ה-p-אדיים דומה בטופולוגיה שלו לקבוצת קנטור. בפרט כדור היחידה ב-p-אדיים (תת קבוצה של מספרים p-אדיים המקבילה לקטע [0,1] בממשיים) הומיאומורפי לקבוצת קנטור.
אנליזה לא סטנדרטית[עריכת קוד מקור | עריכה]
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- sci.math FAQ: Why is 0.9999... = 1?
- גדי אלכסנדרוביץ', ...0.999 שווה 1, באתר "לא מדויק", 7 ביוני 2008
- אלון עמית, טרחנים כפייתיים במתמטיקה, באתר "האייל הקורא"
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ sci.math
- ^
- ^ ראו לדוגמה sci.math FAQ: Why is 0.9999...=1?, גדי אלכסנדרוביץ', ...0.999 שווה 1, באתר "לא מדויק", 7 ביוני 2008
| מספרים טבעיים | ||||||||||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||||||||
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |||||||||||||||
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | |||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | |||||||||||||||
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | |||||||||||||||
| 50 | 51 | 52 | 53 | 54 | ||||||||||||||||||||
| ||||||||||||||||||||||||
| אחרים | ||||||||||||||||||||||||
| שמות מספרים | ...0.999 | 666 | 1089 | 1729 | קבוע קפרקר | גוגול | גוגולפלקס | מספר גרהאם | ||||||||||||||||||||||||





















































![{\displaystyle [0,1]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/98ef6fb8c5d9b34f4ba677930a956bd62270f9a2)
![{\displaystyle \{0.\dots ,9\}^{\omega }\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4b186950ffd4697ac2455711312c8fdd34edcb0)



