משפט רול

המחשה של המשפט: הקו הירוק, שהוא המשיק לגרף הפונקציה בנקודה c, מקביל לקו האדום המחבר את הקטע [a,b] ולציר ה-x.

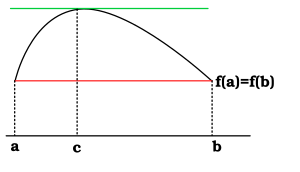
בחשבון אינפיניטסימלי, משפט רול (על שם מטר רול), הוא משפט בסיסי העוסק בתכונה של פונקציות רציפות וגזירות בקטע סגור. המשפט אומר כי אם פונקציה רציפה בקטע סגור והיא גם גזירה בו (פרט אולי לקצותיו) וערכיה בשני קצוות הקטע זהים, קיימת נקודה בה נגזרתה מתאפסת, כלומר המשיק לגרף הפונקציה בנקודה זו הוא קו מאוזן.

מבחינה לא פורמלית ניתן לתאר את המשפט כך: אם מצוירת פונקציה בין שתי נקודות באותו גובה (אותו ערך של y) בלי שהעיפרון מורם מהדף ובלי היווצרות 'שפיצים', תהיה לפחות נקודה אחת שבה העיפרון נע בדיוק במקביל למערכת הצירים, ולא בשיפוע כלשהו.

המשפט

תהי $\ f$ פונקציה רציפה בקטע הסגור $\left[a,b\right]$ וגזירה בקטע הפתוח $\left(a,b\right)$ כך שמתקיים $\ f(a)=f(b)$. אז קיימת נקודה $\ c\in (a,b)$ כך שמתקיים $\ f'(c)=0$.

הוכחה

על פי משפט ויירשטראס השני, פונקציה רציפה בקטע סגור מקבלת בו מינימום ומקסימום. אם גם המינימום וגם המקסימום מתקבלים בקצוות (אשר, לפי הנתון, שווים בערכם) הרי שהפונקציה קבועה, והנגזרת שלה היא אפס בכל נקודה. אחרת, נניח למשל שהמקסימום מתקבל בתוך הקטע. אז על פי משפט פרמה ערך הנגזרת בנקודת המקסימום הוא 0, כנדרש. עבור מינימום שמתקבל בתוך הקטע ההוכחה זהה.

הכללות

אף שהמשפט נדמה כמעט טריוויאלי, קיימות לו שתי הכללות שימושיות מאוד: משפט הערך הממוצע של לגראנז' ומשפט הערך הממוצע של קושי.