נפח – הבדלי גרסאות
מ ←פתיח |
מ בקטנה |
||
| שורה 1: | שורה 1: | ||
| ⚫ | |||
{{בעבודה מתמשכת}} |
{{בעבודה מתמשכת}} |
||
| ⚫ | |||
'''נפח''' הוא תכונת מדידה של עצם המאופיינת בהשתרעותו על פני יותר משני [[ממד (פיזיקה)|ממדים]]. מידת הנפח של עצם היא כמות המקום התפוסה על ידיו ב[[מרחב תלת-ממדי]]. בשפת הדיבור, כאשר מתייחסים לנפח של כלי קיבול (כמו [[בקבוק]], דלי, [[משורה]]), מתכוונים לקיבולת שלו ולא לנפח שתופס הכלי עצמו. ביחידות [[מערכת היחידות הבינלאומית]] ה[[פיזיקה|פיזיקליות]], הנפח נמדד ב[[מטר מעוקב|מטרים מעוקבים]]. |
'''נפח''' הוא תכונת מדידה של עצם המאופיינת בהשתרעותו על פני יותר משני [[ממד (פיזיקה)|ממדים]]. מידת הנפח של עצם היא כמות המקום התפוסה על ידיו ב[[מרחב תלת-ממדי]]. בשפת הדיבור, כאשר מתייחסים לנפח של כלי קיבול (כמו [[בקבוק]], דלי, [[משורה]]), מתכוונים לקיבולת שלו ולא לנפח שתופס הכלי עצמו. ביחידות [[מערכת היחידות הבינלאומית]] ה[[פיזיקה|פיזיקליות]], הנפח נמדד ב[[מטר מעוקב|מטרים מעוקבים]]. |
||
הנפח של קובייה בעלת אורך צלע <math> |
הנפח של קובייה בעלת אורך צלע <math>L</math> הוא <math>L^3</math>. את הנפח של גופים מסובכים יותר אפשר לחשב באמצעות "שיטת המיצוי" שהמציא ארכימדס, שעל-פיה מחלקים את הגוף למרכיבים [[אינפיניטסימל]]יים שנפחם ידוע, ומחברים את הנפחים. מנקודת מבט מודרנית, זוהי [[אינטגרל|אינטגרציה]] נפחית על הגוף. |
||
[[תורת המידה]] ה[[מתמטיקה|מתמטית]] מכלילה את מושג הנפח התלת-ממדי (ואת מושג השטח הדו-ממדי) לאופנים כלליים יותר של שיוך "מידה" למקומות או עצמים במרחב. על-פי גישה זו, הנפח של גוף חד-ממדי, כגון [[ישר|קו]], או לגוף דו-ממדי, כגון [[ריבוע]], הוא [[אפס (מספר)|אפס]]. את תורת המידה מגביל [[הפרדוקס של בנך-טרסקי]], המראה שאי אפשר להגדיר באופן עקבי את הנפח של כל הגופים המרחביים. |
[[תורת המידה]] ה[[מתמטיקה|מתמטית]] מכלילה את מושג הנפח התלת-ממדי (ואת מושג השטח הדו-ממדי) לאופנים כלליים יותר של שיוך "מידה" למקומות או עצמים במרחב. על-פי גישה זו, הנפח של גוף חד-ממדי, כגון [[ישר|קו]], או לגוף דו-ממדי, כגון [[ריבוע]], הוא [[אפס (מספר)|אפס]]. את תורת המידה מגביל [[הפרדוקס של בנך-טרסקי]], המראה שאי אפשר להגדיר באופן עקבי את הנפח של כל הגופים המרחביים. |
||
| שורה 70: | שורה 70: | ||
==יחידות מידה לנפח== |
==יחידות מידה לנפח== |
||
בשימוש יומיומי נהוג להשתמש ב: |
בשימוש יומיומי נהוג להשתמש ב[[יחידת מידה|יחידות המידה]] הבאות למדידת נפח: |
||
* [[ליטר]] |
* [[ליטר]] |
||
**מיליליטר (מ"ל) - אלפית הליטר |
**מיליליטר (מ"ל) - אלפית הליטר |
||
גרסה מ־17:40, 21 בפברואר 2021
ערך זה נמצא בתהליך עבודה מתמשך.
הערך פתוח לעריכה. | ||
| ערך זה נמצא בתהליך עבודה מתמשך. הערך פתוח לעריכה. | |
נפח הוא תכונת מדידה של עצם המאופיינת בהשתרעותו על פני יותר משני ממדים. מידת הנפח של עצם היא כמות המקום התפוסה על ידיו במרחב תלת-ממדי. בשפת הדיבור, כאשר מתייחסים לנפח של כלי קיבול (כמו בקבוק, דלי, משורה), מתכוונים לקיבולת שלו ולא לנפח שתופס הכלי עצמו. ביחידות מערכת היחידות הבינלאומית הפיזיקליות, הנפח נמדד במטרים מעוקבים.
הנפח של קובייה בעלת אורך צלע הוא . את הנפח של גופים מסובכים יותר אפשר לחשב באמצעות "שיטת המיצוי" שהמציא ארכימדס, שעל-פיה מחלקים את הגוף למרכיבים אינפיניטסימליים שנפחם ידוע, ומחברים את הנפחים. מנקודת מבט מודרנית, זוהי אינטגרציה נפחית על הגוף.
תורת המידה המתמטית מכלילה את מושג הנפח התלת-ממדי (ואת מושג השטח הדו-ממדי) לאופנים כלליים יותר של שיוך "מידה" למקומות או עצמים במרחב. על-פי גישה זו, הנפח של גוף חד-ממדי, כגון קו, או לגוף דו-ממדי, כגון ריבוע, הוא אפס. את תורת המידה מגביל הפרדוקס של בנך-טרסקי, המראה שאי אפשר להגדיר באופן עקבי את הנפח של כל הגופים המרחביים.
נוסחאות נפח של גופים נפוצים
| גוף | נוסחת הנפח | משתנים |
|---|---|---|
| קובייה | 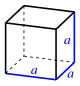
| |
| תיבה | 
| |
| מנסרה
( הוא שטח הבסיס) |
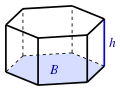
| |
| פירמידה
( הוא שטח הבסיס) |
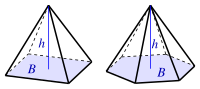
| |
| מקבילון |
|

|
| ארבעון משוכלל | 
| |
| כדור | 
| |
| אליפסואיד | 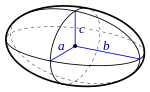
| |
| גליל | 
| |
| חרוט | 
| |
| טורוס | 
| |
| גוף סיבוב | 
|
יחידות מידה לנפח
בשימוש יומיומי נהוג להשתמש ביחידות המידה הבאות למדידת נפח:
- ליטר
- מיליליטר (מ"ל) - אלפית הליטר
- מטר מעוקב (מ"ק)
- גלון
- רגל מעוקבת
- (בהקשר של מאגרי גז טבעי): מיליארד רגל מעוקבת (BCF)
- (בהקשר של מאגרי גז טבעי): טריליון רגל מעוקבת (TCF).
















