פונקציית גמא

פונקציית גמא היא פונקציה מרוכבת מֶ‏רוֹ‏מורפית, המרחיבה את מושג ה"עצרת" לכל המישור המרוכב: לכל מספר טבעי $\ n=1,2,\dots$, הפונקציה מקבלת את הערך $\ \Gamma (n)=(n-1)!$.

הפונקציה הוגדרה לראשונה על ידי לאונרד אוילר באמצע המאה ה-18, אך הסימון של הפונקציה באות $\ \Gamma$ נכנס לשימוש בעקבות עבודתו של לז'נדר. גאוס הציע גרסה מעט שונה של פונקציית גמא, $\ \Pi (z)=\Gamma (z+1)$, לה הוא קרא "פונקציית פאי", אלא שהסימון של לז'נדר הועדף בצרפת, ובעקבות זאת גם בשאר העולם.

הפונקציה מוגדרת במחצית הימנית של המישור המרוכב באמצעות האינטגרל $\Gamma (z)=\int _{0}^{\infty }t^{z-1}\,e^{-t}\,dt$.

לפונקציית גמא קטבים (פשוטים) בנקודות $\,z=0,-1,-2,\dots$ בלבד, ואין לה שורשים. הפונקצייה מקיימת את המשוואה הפונקציונלית $\ \Gamma (z+1)=z\Gamma (z)$, המסבירה את הקשר לפונקציית העצרת, ועוד זהויות פונקציונליות רבות אחרות.

הגדרה

פונקציית גמא מוגדרת על ידי האינטגרל הבא:

$\Gamma (z)=\int _{0}^{\infty }t^{z-1}\,e^{-t}\,dt$

וזאת לכל $\ z\in \mathbb {C}$ המקיים $\,Re(z)>0$. פונקציה זו מתלכדת עם הפונקציה המוגדרת באמצעות הגבול $\ \Gamma (z)=\lim _{n\rightarrow \infty }{\frac {1\cdot 2\cdots n}{z\cdot (z+1)\cdots (z+n-1)}}(n+1)^{z-1}$, המוגדר היטב לכל $\ z\neq 0,-1,-2,\dots$. משום כך, הפונקציה השניה מהווה המשכה אנליטית של האינטגרל לפונקציה מרומורפית.

תכונות

הקשר לפונקציית עצרת

גרף של פונקציית גמא על הישר הממשי

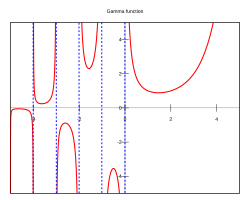
ניתן להראות שעבור מספרים טבעיים, פונקציית גמא שווה לפונקציית העצרת.

אם $\,n$ הוא חיובי ושלם, אזי $\Gamma (n)=\int _{0}^{\infty }t^{n-1}\,e^{-t}\,dt=(n-1)!$, כי על ידי ביצוע אינטגרציה בחלקים, אפשר להראות כי $\,\Gamma (n+1)=n\Gamma (n)$, ומאחר ש-$\,\Gamma (1)=1$ נקבל כי $\,\Gamma (n+1)=n\Gamma (n)=\ldots =n!\Gamma (1)=n!\,$ לכל מספר טבעי $\,n$.

זהויות אחרות

זהות חשובה אחת לפונקציית גמא היא נוסחת השיקוף: $\ \Gamma (1-z)\Gamma (z)={\pi \over \sin \pi z}$.

מכאן נובע כי $\Gamma \left({\frac {1}{2}}\right)^{2}={\pi \over \sin \pi /2}=\pi$, ולכן $\Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}$.

זהות חשובה אחרת היא נוסחת הכפל של גאוס:

$\Gamma (z)\;\Gamma \left(z+{\frac {1}{k}}\right)\;\Gamma \left(z+{\frac {2}{k}}\right)\cdots \Gamma \left(z+{\frac {k-1}{k}}\right)=(2\pi )^{(k-1)/2}\;k^{1/2-kz}\;\Gamma (kz)\,\!$

גרף של הערך המוחלט של פונקציית גמא במישור המרוכב.
באיור זה ניתן לראות בבירור את הקטבים של הפונקציה

לפונקציית גמא יש קוטב ב $\,z=-n$ לכל $\,n$ טבעי. בנקודה זאת נתון גם ש:

$\operatorname {Res} (\Gamma ,-n)={\frac {(-1)^{n}}{n!}}.$

המכפלה האינסופית הבאה, כפי שהראה ויירשטראס, נכונה לכל $\,z$ מרוכב, אשר אינו שלם אי-חיובי:

$\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n}$

כאשר $\,\gamma$ הוא "קבוע אוילר".

משפט בוהר-מולרופ

משפט בוהר-מולרופ (Bohr–Mollerup theorem) הוא משפט המאפיין את פונקציית גמא. המשפט קרוי של-שמם של המתמטיקאים הדנים הארלד בוהר ויוהאן מולרופ שהוכיחו אותו.

משפט: פונקציית גמא הממשית המוגדרת לכל $\,x>0$ על ידי $\Gamma (x)=\int _{0}^{\infty }t^{x-1}e^{-t}\,dt$ היא הפונקציה היחידה $\,f$ בקרן $(0,\infty )$ המקיימת:

1. $\,f(1)=1$
2. $f(x+1)=xf(x)\ {\mbox{for}}\ x>0$
3. $\,f$ היא פונקציה לוג-קמורה

אחת ההוכחות לנוסחת סטירלינג משתמשת במשפט זה. במסגרת ההוכחה בונים פונקציה המקיימת את שלושת התנאים במשפט בוהר-מולרפ, ולכן פונקציה זו היא בהכרח פונקציית גמא.

ראו גם

• פונקציית בטא

קישורים חיצוניים

• פונקציית גמא באתר Wolfram mathworld
• מחשבון לפונקציית גמא