רשת מיון – הבדלי גרסאות

תוכן שנמחק תוכן שנוסף

בשורה

גרסה מ־23:26, 15 במאי 2018

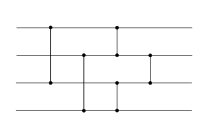
איור 1: רשת מיון פשוטה לארבעה קלטים בעלת ארבעה חוטים וחמש יחידות השוואה.

במדעי המחשב, רשת השוואה היא מבנה מתמטי הכולל רשת של "חוטים" שעליהם "זורמים" ערכים, ושל יחידות השוואה המחברות בין זוגות חוטים ומחליפות בין הערכים שבהם כדי לסדרם, אם יש צורך. כאשר רשת השוואה מסויימת מצליחה לסדר כל קבוצת ערכים המוכנסת אליה היא נקראת רשת מיון.

מיון בעזרת רשתות מיון שונה משיטות מיון אחרות בכך שכל רשת יכולה למיין מספר קבוע מראש של קלטים. כלומר אי אפשר לקחת רשת ולהשתמש בה לכל בעיית מיון. היתרון הגדול של רשת מיון הוא שהיא נוחה למיקבול - כלומר לחלוקה למשימות היכולות להתבצע במקביל. כך, כשהמיון נעשה על מחשב המאפשר בצוע מקבילי ניתן להגיע באופן מעשי לביצועים של $O(log^{2}n)$ , להבדיל מהגבול הנמוך האפשרי תאורטית עבור מיון סדרתי של $O(n\ log\ n)$ ). ישנן גם רשתות הנותנות סיבוכיות תאורטית טובה יותר (לוגריתמית) אך עם קבועים גבוהים מדי בכדי לאפשר שימוש מעשי.

רשתות מיון הוצגו לראשונה ב1954 על ידי ארמסטרונג, נלסון, ואו-קונור שהוציאו פטנט על הרעיון^[1]^[2].

הגדרה

איור 2: הדגמה של הפעלה של יחידת השוואה ברשת השוואה.

רשת השוואה כוללת שני סוגי רכיבים - חוטים ויחידות השוואה. על החוטים ניתן לחשוב כמעבירים ערכים ה"זורמים" עליהם בו זמנית משמאל לימין. כל יחידת השוואה מקשרת שני חוטים. כשזוג ערכים "מגיע" ליחידת השוואה, היחידה מחליפה את הערכים אם ורק אם הערך הגבוה גדול מהערך הנמוך (במילים אחרות, יחידות ההשוואה מעבירות ערכים גבוהים למטה וערכים נמוכים למעלה)^[3].

בעזרת נוסחה ניתן להגדיר שאם החוט העליון נושא ערך $x$ והתחתון ערך $y$ אז אחרי המפגש עם יחידת ההשוואה הערכים על החוטים יהיו $x'=min(x,y)$ ו $y'=max(x,y)$ בהתאמה. רשת השוואה כזאת שתצליח להוציא (בצד ימין) ערכים ממוינים עבור כל סדר של ערכי קלט (בצד שמאל) נקראת רשת מיון.

הפעלה מלאה של רשת מיון פשוטה מופיעה באיור להלן. קל לראות שרשת זו מצליח למיין כל קלט אפשרי של ארבעה מספרים. שימו לב שארבע יחידות ההשוואה הראשונות "ישקיעו" את הערך הגדול למטה ו"יציפו" את הערך הקטן למעלה. היחידה האחרונה פשוט ממיינת את שני הערכים האמצעיים.

עומק ויעילות

היעילות של רשת מיון יכולה להמדד ב"גודלה" - כלומר במספר יחידות ההשוואה שבה, או ב"עומקה" - כלומר במספר המקסימלי של יחידות ההשוואה שערך כלשהו עלול להזדקק לעבור דרכם. חלק מההשוואות ברשת יכולות להתבצע במקביל - כפי שמסומן על ידי יחידות השוואה הממוקמות על אותו קו אנכי. אם מניחים שכל השווה לוקחת יחידת זמן אזי ניתן לראות שעומק הרשת שווה לזמן הדרוש לבצוע המקבילי של המיון^[3].

בניית רשת מיון על ידי הוספת ערכים או על ידי בחירתם

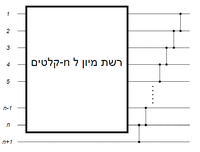
לכל מספר נתון של קלטים ניתן לבנות רשת מיון עם מספר מתאים של חוטים באופן רקורסיבי על ידי הוספת חוט לרשת קטנה יותר. נניח שנתונה רשת מיון עם $n$ חוטים (כלומר המצליחה למיין כל קלט של $n$ מספרים). ניתן להרחיב את הרשת (בהשראת מיון הכנסה) על ידי הוספת חוט נוסף ובצוע סדרה של השוואות על החוטים שמוינו על ידי הרשת הנתונה (ראו איור 4). ניתן גם להשיג את המטרה (בהשראת מיון בועות) על ידי "השקעה" מוקדמת של הערך המינימלי ואחר כך מיון שאר הערכים בעזרת הרשת הנתונה (ראו איור 5).

המבנה של שתי הרשתות המתקבלות הוא דומה. למעשה אם מסדרים את ההשוואות הניתנות לבצוע מקבילי זו מעל זו אזי ניתן לראות ששתי הרשתות למעשה זהות. ראו איורים 8-6.

איור 6: הרשת המתקבלת בהשארת מיון הכנסה.
איור 7: הרשת המתקבלת בהשארת מיון בועות.
איור 8: מיקבול הפעולות מראה ששתי הרשתות שקולות.

לרשתות האלה יש עומק של $2n-3$ . זהו שיפור על הסיבוכיות של לפחות $\ \Omega (n\log n)$ פעולות השוואה הדרושות למיון סדרתי במקרה הגרוע. למעשה ניתן לבנות רשתות מיון עם סיבוכיות טובה אף יותר ובעלות עומק של $O(log^{2}n)$ כפי שיתואר להלן.

עקרון אפס-אחד

בכמה מקרים, כמו בבניית רשת על ידי הוספת ערכים או על ידי בחירתם כפי שתורה למעלה, קל להראות שרשת ההשוואה הנוצרת היא רשת מיון. למרות זאת, לגבי רשת כללית ההוכחה שהרשת ממיינת בהצלחה כל קלט אפשר היא משימה קשה. ברשת בעלת $n$ חוטים יש לבדוק $n!$ סידורים אפשריים של ערכים על החוטים. אפשר להקטין מספר זה במידה משמעותית ל $2^{n}$ בעזרת עקרון אפס-אחד. זהו עדיין מספר אקספוננציאלי של בדיקות אך הוא קטן מ- $n!$ לכל $n\geq 4$ , וההבדל הולך וגדל עם $n$ . נראה שלא תמצא דרך יעילה יותר לבעיית הבדיקה אם רשת השוואה היא רשת מיון, אלא אם יסתבר שP=NP, כיוון שבעיה זאת ידועה כבעיה co-NP-שלמה^[4].

עקרון אפס-אחד קובע שאם רשת השוואה מצליחה למיין את כל $2^{n}$ סידורי הקלטים עם הערכים 0 ו 1, אזי היא גם תצליח למיין קלטים עם כל ערך בכלל. הוכחת העקרון בקווים כלליים מראה שאם $f$ היא פונקציה מונוטונית אזי לכל זוג ערכים $x$ ו- $y$ מתקיים $min(f(x),f(y))=f(min(x,y))$ וגם $max(f(x),f(y))=f(max(x,y))$ . מכאן נובע שאם רשת ממפה את ערכי הקלט $x$ ו- $y$ ל $x'$ ו- $y'$ , אזי היא גם תמפה את $f(x)$ ו- $f(y)$ ל $f(x')$ ו- $f(y')$ . אפשר להכליל טענה זאת באינדוקציה ללמה הטוענת שאם רשת ממפה את הקלטים $a_{1},...,a_{n}$ ל $b_{1},...,b_{n}$ , אזי היא גם תמפה את $f(a_{1}),...,f(a_{n})$ ל $f(b_{1}),...,f(b_{n})$ . המשך ההוכחה הוא בבדרך השלילה. נניח שהרשת שמצליחה למיין כל סדרת קלטים של 0 ו-1 לא מצליחה למיין את הסידרה $a_{1},...,a_{n}$ , כלומר קיימים זוג ערכים כך ש $a_{1}<a_{n}$ והרשת מחליפה את ערכיהם שלא כראוי. אם כך, הרשת גם תמיין לא כראוי את סדרת הערכים $f(b_{1}),...,f(b_{n})$ עבור הפונקציה המונוטונית:

f(x)=\left\{{\begin{matrix}1&{\mbox{if}}\ x>a_{i}\\0&{\mbox{otherwise.}}\\\end{matrix}}\right.

זאת בסתירה להנחה שהרשת ממיינת נכון כל סדרת ערכי 0 ו-1. ומכאן שההנחה שעקרון אפס-אחד לא מתקיים אינה נכונה^[3].

עקרון אפס-אחד שימושי גם לבניות של רשתות מיון כיוון שבכל שלב מספיק לוודא שהרשת מצליחה למיין קלטים של 0 או 1.

בניית רשת מיון יעילה

ישנם מספר אלגוריתמים לבניית רשתות מיון פשוטות ויעילות בעלות עומק של $O(log^{2}n)$ (ולכן גם גודל של $O(n\ log^{2}n)$ ) כמו מיון ביטוני^[5], מיון בטשר מיזוג זוגי-אי-זוגי^[6], מיון של, ורשת מיון בזוגות(אנ'). ברשתות אלה נעשה שימוש מעשי.

אפשר גם תיאורטית לבנות רשתות מיון עם עומק מעריכי (לוגריתמי) לכל מספר של קלטים, בעזרת מבנה המכונה רשת AKS, על שם מגליו Ajtai, Komlós , Szemerédi^[7]. זאת היתה תגלית חשובה אך ללא חשיבות מעשית בשל הקבועים החבויים בנוסחת הסיבוכיות שהם ב"הרבה הרבה אלפים"^[3]. זאת, בין השאר, בשל השימוש בגרף מרחיב. גירסה פשוטה יותר של רשת AKS הוצגה על ידי פטרסון^[8] אך גם כאן הקבועים מונעים כל שימוש מעשי. גודריך הציע בניה של רשת מיון בעלת עומק $O(n\ log\ n)$ ^[9]. הקבועים הפעם קטנים בהרבה מאשר ב רשתות AKS, אך עומק של $O(n\ log\ n)$ לא נותן יתרון לבצוע מקבילי.

רשתות מיון אופטימליות

עבור מספרים קטנים של קלטים ניתן לבנות רשתות מיון עם עומק אופטימלי (לבצוע מקבילי ביותר) או גודל אופטימלי (מספר יחידות ההשוואה). רשתות אלה יכולות לשמש כדי לשפר בצועים של רשתות גדולות יותר שנבנו באון רקורסיבי, למשל בשיטת בטשר (ראה מעלה) על ידי עצירה מוקדמת של הרקורסיה והכנסת הרשת האופטימלית^[10].

הטבלה להלן מסכמת את התוצאות האופטימליות המוכרות:

$n$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
עומק^[11]	0	1	3	3	5	5	6	6	7	7	8	8	9	9	9	9	10
גודל, גבול עליון^[12]	0	1	3	5	9	12	16	19	25	29	35	39	45	51	56	60	71
גודל, גבול תחתון (אם שונה) (if different)^[12]											33	37	41	45	49	53	58

שש-עשר הרשתות הראשונות מופיעות בספר "The Art of Computer Programming" של דונלד קנות' במהדורת 1973. האופטימליות של שמונה הרשתות הראשונות הוכחה על ידי פלויד וקנות' בשנות ה-1960, ושל שאר הרשתות רק ב 2014^[13] (הרשתות של 9 ו-10 קלטים הוכחו כאופטימליות ב 1991^[10]).

רשתות מיון בעלות גודל מינימלי ידועות עד 10 קלטים. עבור יותר קלטים ידוע גבול עליון של הגודל כפי שמצויין בטבלה. כל עשר הרשתות הנ"ל היו מוכרות כבר משנת 1969 ושמונה הראשונות היו ידועות כאופטימליות מאז עבודתם של פלויד וקנות', אבל האופטימליות של הרשתות של 9 ו-10 קלטים הוכחה רק בשנת 2014^[12].

נעשו גם נסיונות לבנות רשתות מיון בעזרת אלגוריתמים גנטים: קנות' מזכיר שרשתות מיון עבור 9 ו-11 קלטים נמצאו כך על ידי לורן שוויברט ב2001^[1].

הערות שוליים

^ ¹ ² Knuth, D. E. (1997). The Art of Computer Programming, Volume 3: Sorting and Searching (Second ed.). Addison–Wesley. pp. 219–247. ISBN 0-201-89685-0. Section 5.3.4: Networks for Sorting.
^ תבנית:Cite patent
^ ¹ ² ³ ⁴ Corman, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990) Introduction to Algorithms (1st edition ed.). MIT Press and McGraw-Hill. פרק 28.
^ Parberry, Ian (1991). On the Computational Complexity of Optimal Sorting Network Verification. Proc. PARLE '91: Parallel Architectures and Languages Europe, Volume I: Parallel Architectures and Algorithms, Eindhoven, The Netherlands. pp. 252–269.
^ Corman, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990) Introduction to Algorithms (1st edition ed.). MIT Press and McGraw-Hill. עמ' 650-642.
^ Corman, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990) Introduction to Algorithms (1st edition ed.). MIT Press and McGraw-Hill. עמ' 651.
^ Ajtai, M.; Komlós, J.; Szemerédi, E. (1983). An $n\ log\ n$ sorting network. STOC '83. Proceedings of the fifteenth annual ACM symposium on Theory of computing. pp. 1–9. doi:10.1145/800061.808726. ISBN 0-89791-099-0.
^ Paterson, M. S. (1990). "Improved sorting networks with $O(log\ n)$ depth". Algorithmica. 5: 75–92. doi:10.1007/BF01840378.
^ Goodrich, Michael (במרץ 2014). "Zig-zag Sort: A Simple Deterministic Data-Oblivious Sorting Algorithm Running in $O(n\ log\ n)$ Time". Proceedings of the 46th Annual ACM Symposium on Theory of Computing - STOC '14. arXiv:1403.2777. doi:10.1145/2591796.2591830. {{cite journal}}: (עזרה)
^ ¹ ² Parberry, Ian (1991). "A Computer Assisted Optimal Depth Lower Bound for Nine-Input Sorting Networks" (PDF). Mathematical Systems Theory. 24: 101–116. doi:10.1007/bf02090393.
^ Codish, Michael; Cruz-Filipe, Luís; Ehlers, Thorsten; Müller, Mike; Schneider-Kamp, Peter (2015). Sorting Networks: to the End and Back Again.
^ ¹ ² ³ Codish, Michael; Cruz-Filipe, Luís; Frank, Michael; Schneider-Kamp, Peter (2014). Twenty-Five Comparators is Optimal when Sorting Nine Inputs (and Twenty-Nine for Ten). Proc. Int'l Conf. Tools with AI (ICTAI). pp. 186–193. arXiv:1405.5754.
^ Bundala, D.; Závodný, J. (2014). "Optimal Sorting Networks". Language and Automata Theory and Applications. Lecture Notes in Computer Science. 8370: 236–247. arXiv:1310.6271. doi:10.1007/978-3-319-04921-2_19. ISBN 978-3-319-04920-5.

[knuth-1] ¹ ² Knuth, D. E. (1997). The Art of Computer Programming, Volume 3: Sorting and Searching (Second ed.). Addison–Wesley. pp. 219–247. ISBN 0-201-89685-0. Section 5.3.4: Networks for Sorting.

[2] תבנית:Cite patent

[אלג-3] ¹ ² ³ ⁴ Corman, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990) Introduction to Algorithms (1st edition ed.). MIT Press and McGraw-Hill. פרק 28.

[parberry-4] Parberry, Ian (1991). On the Computational Complexity of Optimal Sorting Network Verification. Proc. PARLE '91: Parallel Architectures and Languages Europe, Volume I: Parallel Architectures and Algorithms, Eindhoven, The Netherlands. pp. 252–269.

[5] Corman, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990) Introduction to Algorithms (1st edition ed.). MIT Press and McGraw-Hill. עמ' 650-642.

[6] Corman, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990) Introduction to Algorithms (1st edition ed.). MIT Press and McGraw-Hill. עמ' 651.

[7] Ajtai, M.; Komlós, J.; Szemerédi, E. (1983). An $n\ log\ n$ sorting network. STOC '83. Proceedings of the fifteenth annual ACM symposium on Theory of computing. pp. 1–9. doi:10.1145/800061.808726. ISBN 0-89791-099-0.

[8] Paterson, M. S. (1990). "Improved sorting networks with $O(log\ n)$ depth". Algorithmica. 5: 75–92. doi:10.1007/BF01840378.

[9] Goodrich, Michael (במרץ 2014). "Zig-zag Sort: A Simple Deterministic Data-Oblivious Sorting Algorithm Running in $O(n\ log\ n)$ Time". Proceedings of the 46th Annual ACM Symposium on Theory of Computing - STOC '14. arXiv:1403.2777. doi:10.1145/2591796.2591830. {{cite journal}}: (עזרה)

[parberry91-10] ¹ ² Parberry, Ian (1991). "A Computer Assisted Optimal Depth Lower Bound for Nine-Input Sorting Networks" (PDF). Mathematical Systems Theory. 24: 101–116. doi:10.1007/bf02090393.

[codish_end_game-11] Codish, Michael; Cruz-Filipe, Luís; Ehlers, Thorsten; Müller, Mike; Schneider-Kamp, Peter (2015). Sorting Networks: to the End and Back Again.

[codish-12] ¹ ² ³ Codish, Michael; Cruz-Filipe, Luís; Frank, Michael; Schneider-Kamp, Peter (2014). Twenty-Five Comparators is Optimal when Sorting Nine Inputs (and Twenty-Nine for Ten). Proc. Int'l Conf. Tools with AI (ICTAI). pp. 186–193. arXiv:1405.5754.

[bundala_zavodny-13] Bundala, D.; Závodný, J. (2014). "Optimal Sorting Networks". Language and Automata Theory and Applications. Lecture Notes in Computer Science. 8370: 236–247. arXiv:1310.6271. doi:10.1007/978-3-319-04921-2_19. ISBN 978-3-319-04920-5.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

@@ שורה 3: / שורה 3: @@
 מיון בעזרת רשתות מיון שונה משיטות [[מיון (אלגוריתם)|מיון]] אחרות בכך שכל רשת יכולה למיין מספר קבוע מראש של קלטים. כלומר אי אפשר לקחת רשת ולהשתמש בה לכל בעיית מיון. היתרון הגדול של רשת מיון הוא שהיא נוחה למיקבול - כלומר לחלוקה למשימות היכולות להתבצע במקביל. כך, כשהמיון נעשה על מחשב המאפשר בצוע מקבילי ניתן להגיע באופן מעשי לביצועים של <math>O(log^2n)</math>, להבדיל מהגבול הנמוך האפשרי תאורטית עבור מיון סדרתי של <math>O(n\ log\ n)</math>). ישנן גם רשתות הנותנות סיבוכיות תאורטית טובה יותר (לוגריתמית) אך עם קבועים גבוהים מדי בכדי לאפשר שימוש מעשי.
+רשתות מיון הוצגו לראשונה ב1954 על ידי ארמסטרונג, נלסון, ואו-קונור שהוציאו פטנט על הרעיון<ref name="knuth">{{cite book |first=D. E. |last=Knuth |authorlink=Donald Knuth |title=[[The Art of Computer Programming]], Volume 3: Sorting and Searching |edition=Second |publisher=Addison–Wesley |year=1997 |isbn=0-201-89685-0 |pages=219–247}} Section 5.3.4: Networks for Sorting.</ref><ref>{{cite patent |country=US |number=3029413 |title=Sorting system with {{mvar|n}}-line sorting switch |pubdate=10 April 1962 |fdate= 21 February 1957 |inventor1-first=Daniel G. |inventor1-last=O'Connor |inventor2-first=Raymond J. |inventor2-last=Nelson}}</ref>.
 ==הגדרה==
@@ שורה 58: / שורה 60: @@
 {| class="wikitable" style="text-align: center;"
 |-
-! style="text-align: left;" | {{mvar|n}}
+! style="text-align: right;" | {{mvar|n}}
 | style="width: 20px;" | 1 || style="width: 20px;" | 2 || style="width: 20px;" | 3 || style="width: 20px;" | 4 || style="width: 20px;" | 5 || style="width: 20px;" | 6 || style="width: 20px;" | 7 || style="width: 20px;" | 8 || style="width: 20px;" | 9 || style="width: 20px;" | 10 || style="width: 20px;" | 11 || style="width: 20px;" | 12 || style="width: 20px;" | 13 || style="width: 20px;" | 14 || style="width: 20px;" | 15 || style="width: 20px;" | 16
 |17
 |-
-! style="text-align: left;" | עומק<ref name="codish_end_game">{{cite conference |last1=Codish |first1=Michael |last2=Cruz-Filipe |first2=Luís |last3=Ehlers |first3=Thorsten |last4=Müller |first4=Mike |last5= Schneider-Kamp |first5=Peter |title=Sorting Networks: to the End and Back Again |year=2015}}</ref>
+! style="text-align: right;" | עומק<ref name="codish_end_game">{{cite conference |last1=Codish |first1=Michael |last2=Cruz-Filipe |first2=Luís |last3=Ehlers |first3=Thorsten |last4=Müller |first4=Mike |last5= Schneider-Kamp |first5=Peter |title=Sorting Networks: to the End and Back Again |year=2015}}</ref>
 | 0 || 1 || 3 || 3 || 5 || 5 || 6 || 6 || 7 || 7 || 8 || 8 || 9 || 9 || 9 || 9
 |10
 |-
-! style="text-align: left;" | גודל, גבול עליון<ref name="codish">{{cite conference |last1=Codish |first1=Michael |last2=Cruz-Filipe |first2=Luís |last3=Frank |first3=Michael |last4= Schneider-Kamp |first4=Peter |title=Twenty-Five Comparators is Optimal when Sorting Nine Inputs (and Twenty-Nine for Ten) |conference=Proc. Int'l Conf. Tools with AI (ICTAI) |arxiv=1405.5754 |year=2014 |pages=186–193}}</ref>
+! style="text-align: right;" | גודל, גבול עליון<ref name="codish">{{cite conference |last1=Codish |first1=Michael |last2=Cruz-Filipe |first2=Luís |last3=Frank |first3=Michael |last4= Schneider-Kamp |first4=Peter |title=Twenty-Five Comparators is Optimal when Sorting Nine Inputs (and Twenty-Nine for Ten) |conference=Proc. Int'l Conf. Tools with AI (ICTAI) |arxiv=1405.5754 |year=2014 |pages=186–193}}</ref>
 | 0 || 1 || 3 || 5 || 9 || 12 || 16 || 19 || 25 || 29 || 35 || 39 || 45 || 51 || 56 || 60
 |71
 |-
-! style="text-align: left;" | גודל, גבול תחתון (אם שונה) (if different)<ref name="codish"/>
+! style="text-align: right;" | גודל, גבול תחתון (אם שונה) (if different)<ref name="codish"/>
 |  ||  ||  ||  ||  ||  ||  ||  ||  ||  || 33 || 37 || 41 || 45 || 49 || 53
 |58
 |}
+שש-עשר הרשתות הראשונות מופיעות בספר "The Art of Computer Programming" של [[דונלד קנות']] במהדורת 1973. האופטימליות של שמונה הרשתות הראשונות הוכחה על ידי פלויד וקנות' בשנות ה-1960, ושל שאר הרשתות רק ב 2014<ref name="bundala_zavodny">{{Cite journal| doi = 10.1007/978-3-319-04921-2_19| title = Optimal Sorting Networks| journal = Language and Automata Theory and Applications| volume = 8370| pages = 236–247| series = Lecture Notes in Computer Science| year = 2014| last1 = Bundala | first1 = D. | last2 = Závodný | first2 = J. | isbn = 978-3-319-04920-5| arxiv = 1310.6271}}</ref> (הרשתות של 9 ו-10 קלטים הוכחו כאופטימליות ב 1991<ref name="parberry91">{{cite journal |first=Ian |last=Parberry |title=A Computer Assisted Optimal Depth Lower Bound for Nine-Input Sorting Networks |journal=Mathematical Systems Theory |volume=24 |pages=101–116 |year=1991 |url=http://larc.unt.edu/ian/pubs/9-input.pdf |doi=10.1007/bf02090393}}</ref>).
-שש-עשר הרשתות הראשונות מופיעות בספר "The Art of Computer Programming" של [[דונלד קנות']] במהדורת 1973. האופטימליות של
+רשתות מיון בעלות גודל מינימלי ידועות עד 10 קלטים. עבור יותר קלטים ידוע גבול עליון של הגודל כפי שמצויין בטבלה. כל עשר הרשתות הנ"ל היו מוכרות כבר משנת 1969 ושמונה הראשונות היו ידועות כאופטימליות מאז עבודתם של פלויד וקנות', אבל האופטימליות של הרשתות של 9 ו-10 קלטים הוכחה רק בשנת 2014<ref name="codish">{{cite conference |last1=Codish |first1=Michael |last2=Cruz-Filipe |first2=Luís |last3=Frank |first3=Michael |last4= Schneider-Kamp |first4=Peter |title=Twenty-Five Comparators is Optimal when Sorting Nine Inputs (and Twenty-Nine for Ten) |conference=Proc. Int'l Conf. Tools with AI (ICTAI) |arxiv=1405.5754 |year=2014 |pages=186–193}}</ref>.
+נעשו גם נסיונות לבנות רשתות מיון בעזרת [[אלגוריתם גנטי|אלגוריתמים גנטים]]: קנות' מזכיר שרשתות מיון עבור 9 ו-11 קלטים נמצאו כך על ידי לורן שוויברט ב2001<ref name="knuth"/>.
 ==הערות שוליים==