דרגה (תורת הגרפים)

בתורת הגרפים, דרגה של צומת מתארת את מספר הקשתות המקושרות לצומת מסוים. זהו המידע הבסיסי ביותר שאפשר למסור על צומת בגרף, משום שהוא מתאר את תמונת העולם המקומית של הקודקודים שלו. דרגה של צומת מסומנת כ־.
גרף שדרגות כל הצמתים בו שוות ל- נקרא גרף -רגולרי, ונהוג לומר שדרגתו של הגרף היא .
גרפים בלתי-מכוונים[עריכת קוד מקור | עריכה]
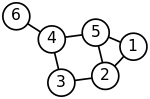
בגרף בלתי מכוון, הדרגה של צומת היא מספר הקשתות היוצאות ממנו. במקרה כזה, לולאה נספרת כשתי קשתות, כפי שרואה אותה מעגל קטן סביב הצומת. מכאן נובע, כי דרגת צומת אשר בו קיימת לולאה הנה .
הדרגות של הצמתים בגרף משמאל מתוארות בטבלה הבאה:
| צומת | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| דרגה | 2 | 3 | 2 | 3 | 3 | 1 |
גרפים מכוונים[עריכת קוד מקור | עריכה]
בגרפים מכוונים, לכל קשת יש שני קצוות שונים: ה"ראש" (המסומן על ידי ראש החץ), וה"זנב" (ממנו יוצאת הקשת). לצורך חישוב דרגה של צומת, כל סוג של קצה נספר בנפרד.
דרגת כניסה[עריכת קוד מקור | עריכה]
דרגת הכניסה (אנגלית: indegree) של צומת היא סך הקשתות אשר הקצה שלהן המשויך לצומת הוא מסוג "ראש" (כמה קשתות נכנסות לצומת).
דרגת הכניסה מסומנת ב־ .
דרגת יציאה[עריכת קוד מקור | עריכה]
דרגת היציאה (אנגלית: outdegree) של צומת היא סך הקשתות אשר הקצה שלהן המשויך לצומת הוא מסוג "זנב" (כמה קשתות יוצאות מהצומת).
דרגת היציאה מסומנת ב - .
דוגמה[עריכת קוד מקור | עריכה]

דרגות הכניסה והיציאה של הצמתים בגרף משמאל מתוארות בטבלה הבאה:
| צומת | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| דרגת כניסה | 0 | 2 | 2 | 1 |
| דרגת יציאה | 2 | 0 | 2 | 1 |
ערכי דרגה מיוחדים[עריכת קוד מקור | עריכה]

- אם לצומת יש דרגה 0, הוא נקרא צומת מבודד.
- אם לצומת יש דרגה 1, הוא נקרא עלה. בכל עץ לא טריוויאלי יש לפחות שני עלים.
- אם לצומת מתקיים , הצומת נקרא מקור. זאת מאחר שהוא מהווה מקור לכל הקשתות העוברות דרכו.
- אם לצומת מתקיים , הצומת נקרא בור.
הגדרה פורמלית[עריכת קוד מקור | עריכה]
ניתן להגדיר פורמלית את דרגתו של צומת בגרף בלתי-מכוון ללא קשתות מקבילות כש־ הוא אוסף הצמתים ו־ הוא אוסף הקשתות, באופן הבא:
כלומר, הגודל של קבוצת כל הצמתים שקיימת קשת בינם לבין .
באופן דומה ניתן להגדיר את דרגות הכניסה והיציאה בגרף מכוון ללא קשתות מקבילות:
נוסחת סכום הדרגות קובעת שסכום הדרגות של כל הצמתים בגרף שווה ל: , זאת מאחר שלכל קשת יש שני קצוות, וכך היא תורמת 2 לסכום הדרגות בגרף. מסקנה מכך (למת לחיצות הידיים) היא שבכל גרף יש מספר זוגי של צמתים מדרגה אי-זוגית.
סדרת דרגות[עריכת קוד מקור | עריכה]

סדרת הדרגות של גרף לא מכוון עם צמתים היא סדרה לא עולה של דרגות הצמתים של הגרף.
לגרפים איזומורפים יש את אותה סדרת דרגות. אבל התכונה ההפוכה לא מתקיימת, אם לשני גרפים אותה סדרת דרגות הם לא בהכרח איזומורפיים.
סדרה נקראת גרפית אם קיים גרף שהיא סדרת הדרגות שלו. בעיית סדרת הדרגות היא למצוא גרף (או את כל הגרפים) שסדרת הדרגות שלו שווה לסדרה נתונה כלשהי. קיים אפיון של הסדרות הגרפיות (אנ')[1] המוביל לאלגוריתם החלטה בזמן פולינומי האם סדרה נתונה היא גרפית והגרף הוא גרף פשוט (אם הגרף יכול להכיל לולאות וקשתות מקבילות ניתן לבנות גרף שכזה לכל סדרה לא יורדת שסכומה זוגי, ולא ניתן לבנות גרף שכזה לכל סדרה שסכומה אי-זוגי (נובע ישירות מלמת לחיצות הידיים)).
קישורים חיצוניים[עריכת קוד מקור | עריכה]
ביאורים[עריכת קוד מקור | עריכה]
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ P. Erdős, T. Gallai, Graphs with prescribed degrees of vertices, Mat. Lopak 11, 1960, עמ' 264-274
| נושאים בתורת הגרפים | ||
|---|---|---|
| הגדרות | צומת • קשת • דרגה • מסלול • מרחק | |
| מבנים | גרף • גרף ממושקל • מעגל • גרף מקרי • היפרגרף • מולטיגרף • עץ • קומפלקס | |
| בניות וטיפוסים | גרף משלים • גרף קיילי • גרף שלם • גרף תחרות • עץ פורש • רשת זרימה • שידוך | |
| תכונות | גרף n-צביע • גרף דו-צדדי • גרף מישורי • גרף מרחיב • גרף רגולרי • גרף קשיר • עץ בינומי • עץ פורש מינימלי | |

















