שחור ופתור

שחור ופתור (באנגלית: Nonogram או Griddler, ביפנית: 絵かきロジック, כלומר "ציור הגיון"; נהגה: ekaki-rojiku) היא חידת היגיון גרפית שבה יש לגלות ציור חבוי בטבלת משבצות לבנה על ידי השחרה של חלק מהן.
החידה מכונה גם תשבץ יפני, אך בישראל אינה מקובלת כתשבץ.
בראש כל טור ושורה של הטבלה, רשומות סדרות של מספרים המייצגים רצפים של משבצות צבועות באותו הטור או באותה השורה, בסדר הנתון. לדוגמה- "1 3 6" בראש שורה (ראו שורה שמינית מלמטה בדוגמה משמאל) משמעו שיש בטור שלושה רצפים נפרדים של משבצות שצריכות להיצבע, רצף אחד של שש משבצות, אחריו אך במרחק לא ידוע ממנו, רצף נוסף של שלוש משבצות ולאחריו משבצת צבועה אחת ואחרונה לשורה זו. הפתירה נעשית על ידי הצלבה של הטורים והשורות.
ישנם מספר סוגים לחידה זו, למשל תשבץ שחור לבן לעומת תשבץ צבעוני. בתשבץ שחור לבן חייב להיות רווח של לפחות משבצת אחת בין כל קבוצה מושחרת, ובתשבץ הצבעוני שתי קבוצות בצבעים שונים יכולות להיות סמוכות זו לזו. משבצותיהם של חלק מהתשבצים עשויות ממשולשים, כך שכל משבצת צריכה לענות על התנאים שקובעות שלוש סדרות של מספרים, לעומת שתי סדרות של מספרים המשפיעות על משבצות ריבועיות. חידה דומה ומעט מורכבת יותר, היא הטרידלר, המורכבת ממשולשים. חידה זו פותרים תוך הצלבה של 3 צדדים, לעומת ההצלבה בין 2 כיוונים בשחור ופתור הרגיל.
שיטות פתרון[עריכת קוד מקור | עריכה]
כדי לפתור את החידה יש לקבוע אילו תאים צבועים ואילו לבנים. קביעת התאים הלבנים חשובה כמו קביעת התאים הצבועים. פותרים משתמשים בדרך כלל בנקודה או באיקס לסימון תאים לבנים.
כמו כן, חשוב לא לנחש. תאים שצובעים או מסמלים כלבנים צריכים להיות רק תאים שאפשר להסיק את מצבם על ידי היגיון. אם מנחשים, הטעות יכולה להתפשט לכל הלוח ולהרוס את הפתרון. בדרך כלל "עולים" על הטעות בשלב שכבר קשה לתקן אותה. רק פותרים מתקדמים יכולים לתקן את הטעות ולסיים את החידה.
את החידות הפשוטות ניתן לפתור על ידי חשיבה על שורה (או עמודה) אחת בכל פעם, וקביעה איזה תאים צבועים בשורה זאת ואיזה תאים לבנים. לאחר מכן מנסים עוד שורה (או עמודה) עד לפתירת כל החידה.
חידות קשות יותר עשויות לדרוש מספר "מה אם?". שיטה הכוללת חשיבה על יותר משורה או עמודה אחת. שיטה זאת עובדת על חיפוש סתירות: אם צביעת תא מסוים גורמת לשגיאה בתא אחר ניתן להסיק שתא הנ"ל הוא לבן, ולהפך. שיטה זאת דורשת יותר זמן להתקדמות.
חפיפה[עריכת קוד מקור | עריכה]


את התשבץ מתחילים בדרך כלל מחפיפה. את החפיפה מבצעים כך: בוחרים מספר כלשהו, ובודקים עד לאן יגיע אם יהיה "מיושר" עד הסוף שמאלה, לאן יגיע אם יהיה "מיושר" עד הסוף ימינה. המשבצות החופפות בכל מקרה נצבעות. שיטת החפיפה מועילה בעיקר במקרים של מספר גדול, או של מספרים רבים.
בדוגמה הראשונה ניתן לראות שבין אם "ניישר" את ה-8 עד הסוף שמאלה, ובין אם "ניישר" את ה-8 עד הסוף ימינה, שש המשבצות המרכזיות יהיו תמיד צבועות.
בדוגמה השנייה ניתן לראות שבכל מקרה שתי משבצות של ה-4 יהיו צבועות, ומשבצת אחת של ה-3. בדרך כלל קשה לעשות זאת בצורה כזאת, אלא סופרים כל מספר לחוד.
חללים פשוטים[עריכת קוד מקור | עריכה]
בשיטה זו, מחפשים תאים שניתן לקבוע שהם לבנים בגלל שלא ניתן למלא אותם על ידי הרצפים. לדוגמה, בשורה של עשרה תאים, כאשר התאים ה-4 וה-9 צבועים והרצפים הם 3 ו-1. הרצף 3 חייב להכיל את התא ה-4 והרצף 1 חייב להיות בתא ה-9.

- הרצף 1 הוא מלא וניתן לסמן את התאים הסמוכים לו כלבנים.
- הרצף 3 חייב להיות איפשהו בין התא השישי לתא השני, כי הרצף מכיל את התא הרביעי; כך על התאים ה-1 וה-7 לא יכול להימצא שום רצף וניתן לסמנם כלבנים.
אילוצים[עריכת קוד מקור | עריכה]

לדוגמה, בשורה של 10, כאשר אנו יודעים שהתא ה-5 וה-7 הם לבנים, והרצפים הם 3 ו-2, ניתן להסיק ש:
- הרצף 3 חייב להיות בתאים 1-4, כי הוא לא נכנס בשום מקום אחר. (לאחר מכן ניתן לצבוע את התאים 2 ו-3 לפי שיטת החפיפה).
- הפער (תא 6) בין התאים שאנו יודעים שהם לבנים קטן מדי מכדי להכיל את הרצפים ולכן ניתן לסמנו כלבן.
- הרצף 2 חייב להיות בתאים 8-10. (לאחר מכן ניתן לצבוע את התא ה-9 לפי שיטת החפיפה).
הדבקה[עריכת קוד מקור | עריכה]
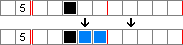
לדוגמה, בשורה של 10 משבצות, כאשר התא השלישי צבוע ויש רצף של 5, ניתן לצבוע את התאים ה-4 וה-5 בגלל הגבול.

שימו לב: ניתן להשתמש בשיטה זו גם באמצע השורה, רחוק מההתחלה, במצבים הבאים:
- תא שאנו יודעים שהוא ריק יכול לשמש כגבול של הרצף הראשון במקרה שהרצף חייב להיות מימינו.
- הרצף הנקרא "רצף ראשון" יכול להיות גם רצפים אחרים, אם אנו יודעים שרצף זה חייב להופיע ישר אחרי תא שאנו יודעים שהוא לבן.
חיבור והפרדה[עריכת קוד מקור | עריכה]
- תא לבן, אם חיבור שלו עם התאים לידו יצור רצף גדול מדי.
- תא צבוע, אם הפיכתו לתא לבן תיצור שני רצפים קטנים מדי או שאין עוד תאים.

לדוגמה, בשורה של 15 תאים, כאשר התאים ה-3, ה-4, ה-6, ה-7, ה-11 וה-13 צבועים, ויש רצפים של 5, 2 ו-2:
- בגלל הרצף הראשון של 5, ניתן לקבוע שהתא ה-5 צבוע, משום שאם הוא יהיה לבן אז הרצף הראשון יהיה רק 4.
- בגלל שני הרצפים של ה-2, ניתן לדעת שהתא ה-12 הוא תא לבן, משום שאם הוא יהיה צבוע הוא יצור רצף של 3.
שימו לב: בתמונה צורפו 2 רצפים של 2, אף על פי שאותם מצרפים על ידי טכניקת ההדבקה.
פיסוק[עריכת קוד מקור | עריכה]
כדי לפתור את החידה, חשוב בדרך כלל גם לפסק כל רצף של תאים צבועים עם תאים המסומנים כלבנים, כפי שתואר לעיל בשיטת חללים פשוטים. פיסוק מוביל בדרך כלל ליותר אילוצים ועשוי להיות חשוב לפתירת החידה.
הערה: הדוגמאות לעיל לא עשו זאת כדי לשמור על פשטות.
כספית[עריכת קוד מקור | עריכה]

כספית היא מקרה מיוחד של טכניקת חללים פשוטים. שמה של הטכניקה הגיע מהדרך שבה הכספית "נמשכת" בחזרה מצדדי המיכל.
אם יש תא צבוע בשורה שהמרחק שלו מהגבול שווה למספר התיבות של הרצף הראשון, התא הראשון יהיה לבן. הסיבה לכך היא שהתא הראשון משמאל לא יכול להיות שייך לרצף. יתר על כן, אם יש עוד תאים צבועים מימין לתא האמור, מספר התאים הלבנים יהיה כמספר התאים, דבר הנקבע על ידי שימוש בשיטה זו מספר פעמים.
סתירות[עריכת קוד מקור | עריכה]
חלק מהחידות הקשות יותר עשויות לדרוש חשיבה יותר מתקדמת מהשיטות לעיל. כאשר השיטות לעיל ממוצות, חיפוש סתירות עשוי לעזור. מומלץ להישתמש בעיפרון כדי להקל את התיקון. חיפוש הסתירות כולל:
- סימון תא מסוים כצבוע (או כלבן).
- פתירת החידה בשיטות המצוינות לעיל ככל האפשר.
- אם מוצאים שגיאה, התא שסומן כצבוע אינו צבוע אלא לבן בוודאות. (או שהוא צבוע אם סימנו בהתחלה שהתא ריק).
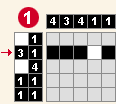
בדוגמה זו אנו מנסים לצבוע את התא השלישי בשורה הראשונה מה שמכריח את התא הראשון בשורה להיות לבן. בעקבות כך אנו צובעים את התא הרביעי בעמודה הראשונה (שיטת החפיפה). לאחר מכן אנו צובעים את התאים ה-2 וה-3 בשורה הרביעית (שיטת ההדבקה). אך צביעת התא השלישי גורמת לסתירה בעמודה השלישית, ולכן אנו מסיקים שהתא השלישי בשורה הראשונה הוא לבן.
הבעיה בשיטה זאת היא שלא ידוע באיזה תא מומלץ לנסות לנחש. בדרך כלל רק כמה תאים מובילים להתקדמות והשאר מובילים לקצוות מתים. תאים שמומלץ להתחיל לנחש בהם יכולים להיות:
- תאים שיש להם הרבה שכנים לא מסומנים.
- תאים שנמצאים בגבולות או ליד גוש של תאים שמסומנים שלבנים.
- תאים שנמצאים בשורה (או עמודה) שרוב תאיה מסומנים.
רקורסיה עמוקה יותר[עריכת קוד מקור | עריכה]
חידות מסוימות עשויות לדרוש לנחש יותר על מנת לחפש סתירות. עם זאת שיטה זו אינה פרקטית בגלל האפשרויות הרבות שיש בה. שיטה זו היא מעשית לפתרון עם מחשבים.
מספר רב של שורות[עריכת קוד מקור | עריכה]
בחלק מהמקרים, חשיבה על קבוצה של שורות עשויה להוביל לצעד הבא של הפתרון גם ללא שימוש בשיטת סתירות ורקורסיה עמוקה יותר. עם זאת, מציאת קבוצות כאלה היא בדרך כלל קשה כמו מציאת סתירות.
פתרונות מרובים[עריכת קוד מקור | עריכה]
יש חידות שיש להם כמה פתרונות אפשריים (אחד כזה הוא תמונה של לוח שחמט פשוט). בחידות אלה, בהגדרה כל הפתרונות נכונים, אך לא כולם יוצרים תמונה סבירה.
שחור ופתור במדעי המחשב[עריכת קוד מקור | עריכה]
בעיית שחור ופתור היא בעיה NP-שלמה[1]. לפיכך אין אלגוריתם פולינומי שפותר את כל בעיות שחור ופתור, אלא אם P=NP. עם זאת, עבור מחלקות מסוימות של חידות, כמו אלו עבורן בכל שורה ועמודה יש רצף יחיד של משבצות שחורות, וכל המשבצות השחורות מקושרות, ניתן למצוא פתרון בזמן פולינומי על ידי רדוקציה לבעיית 2-ספיקות[2].
- דוגמה נוספת
-
צעד 1
-
צעד 2
-
צעד 3
-
צעד 4
-
צעד 5
-
צעד 6
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Ueda, Nobuhisa; Nagao, Tadaaki (1996), NP-completeness results for NONOGRAM via Parsimonious Reductions, TR96-0008, Technical Report, Department of Computer Science, Tokyo Institute of Technology
- ^ Brunetti, Sara; Daurat, Alain (2003), "An algorithm reconstructing convex lattice sets", Theoretical computer science 304 (1–3): 35–57, doi:10.1016/S0304-3975(03)00050-1; Chrobak, Marek; Dürr, Christoph (1999), "Reconstructing hv-convex polyominoes from orthogonal projections", Information Processing Letters 69 (6): 283–289, doi:10.1016/S0020-0190(99)00025-3; Kuba, Attila; Balogh, Emese (2002), "Reconstruction of convex 2D discrete sets in polynomial time", Theoretical Computer Science 283 (1): 223–242, doi:10.1016/S0304-3975(01)00080-9.