משפט דזרג
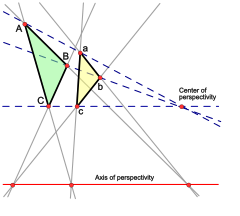
משפט דזרג הוא תכונה אפשרית במרחב פרויקטיבי: כל שני משולשים פרספקטיבים מנקודה הם פרספקטיבים גם ביחס לישר. המשפט אינו נובע מהאכסיומות של הגאומטריה הפרויקטיבית, ולמרות שהוא חל במישור הפרויקטיבי המוגדר מן המישור האוקלידי, יש מישורים פרויקטיבים שאינם מקיימים אותו. מאידך, המשפט חל בכל מרחב פרויקטיבי מממד 3 או יותר. תכונת דזרג מאפשרת להגדיר פעולות על המרחב, באופן כזה שכל מרחב פרויקטיבי המקיים אותה מוגדר על-פי קואורדינטות מעל חוג עם חילוק.
המשפט, המיוחס לז'ראר דזרג (Girard Desargues; 1591–1661), הופיע לראשונה בספר על השימוש המעשי בגאומטריה פרויקטיבית שפרסם חברו ותלמידו Abraham Bosse ב-1648.
המשפט[עריכת קוד מקור | עריכה]
יהי P מרחב פרויקטיבי. שני משולשים ו- הם פרספקטיביים מנקודה אם הישרים נפגשים בנקודה אחת. באופן אינטואיטיבי ניתן לומר, שהמתבונן מנקודת החיתוך אינו יכול להבחין בין שני המשולשים. שני המשולשים האלו יקראו פרספקטיבים ביחס לישר אם החיתוכים של המשכי הצלעות , , , נמצאים על ישר אחד.
משפט דזרג קובע שאם שני משולשים פרספקטיבים ביחס לנקודה אזי הם פרספקטיבים גם ביחס לישר.
המושגים "פרספקטיביות ביחס לנקודה" ו-"פרספקטיביות ביחס לישר" הם מושגים דואליים זה לזה. המשפט הדואלי למשפט דזרג קובע ששני משולשים שהם פרספקטיבים ביחס לישר הם בהכרח פרספקטיבים מנקודה.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- משפט דזרג, באתר MathWorld (באנגלית)
- משפט דזרג, באתר אנציקלופדיה בריטניקה (באנגלית)






