מישור פרויקטיבי
מישור פרויקטיבי הוא מערכת של נקודות וישרים, המקיימת אקסיומות מסוימות. האקסיומות, המונחות ביסודה של הגאומטריה הפרויקטיבית, דומות לאלו של הגאומטריה האוקלידית, פרט לזה שבמקום אקסיומת המקבילים מניחים שכל שני ישרים נפגשים בנקודה. המישור הפרויקטיבי הוא דו-ממדי; ההכללה לממד גבוה נקראת מרחב פרויקטיבי. מישורים ומרחבים פרויקטיביים הם בין המערכות החשובות בגאומטריית חילה.
אם מסירים ממישור פרויקטיבי את אחד הישרים, מתקבל מישור אפיני; ולהפך, אפשר להפוך מישור אפיני למישור פרויקטיבי על ידי הוספת "הישר באינסוף", שהנקודות שלו הן הכיוונים במישור האפיני.
מישורים פרויקטיביים סופיים הם אובייקט חשוב בקומבינטוריקה. הם נלמדו בכלים מתורת החבורות, בעיקר מתחילת שנות ה-60 של המאה העשרים.
הגדרה אקסיומטית[עריכת קוד מקור | עריכה]
מערכת של נקודות וישרים היא מישור פרויקטיבי אם דרך כל שתי נקודות עובר ישר יחיד, כל שני ישרים נפגשים בנקודה, וקיימות 4 נקודות שאף 3 מהן אינן על ישר אחד.
המישור הקלאסי[עריכת קוד מקור | עריכה]
מכל שדה אפשר לבנות מישור פרויקטיבי, אותו מסמנים ב-, באופן הבא. הנקודות הן תת-המרחבים החד-ממדיים במרחב הווקטורי התלת-ממדי , והישרים הם תת-המרחבים הדו-ממדיים; נקודה נמצאת על ישר אם המרחב המתאים לה מוכל במרחב המתאים לו. באופן כזה, כל נקודה אפשר להציג באמצעות שלשת קואורדינטות , המתפרשת כווקטור עד כדי כפל בסקלר. למשל, הנקודה נמצאת על הישר .
זו אמנם בלי ספק הבנייה החשובה ביותר למישור פרויקטיבי, אך יש מישורים רבים אחרים, ובעיית המיון השלמה אינה פתורה אפילו במקרה הסופי.
חבורת הסימטריות[עריכת קוד מקור | עריכה]
סימטריות של מישור פרויקטיבי נקראות קולינאציות (collineations). קולינאציה היא תמורה של הנקודות במישור, המשרה גם תמורה על הישרים (היינו התמונה של קבוצת הנקודות על ישר היא קבוצת הנקודות על ישר). קולינאציה נקראת מרכזית אם יש לה נקודת מרכז (נקודה שכל ישר העובר דרכה נשמר תחת a). תכונה זו שקולה לקיומו של ציר (ישר שכל נקודותיו נשמרות). מבדילים בין שני טיפוסי קולינאציות מרכזיות, לפי שייכותה או אי-שייכותה של נקודת המרכז לציר. אוסף הקולינאציות עם מרכז נתון וציר נתון מהווה חבורה. קולינאציה ב- נקבעת על ידי התמונה של כל נקודה שאינה ב-.
לדוגמה, חבורת הסימטריות של המישור הפרויקטיבי הקלאסי היא חבורת המטריצות . כל קולינאציה מרכזית של צמודה לאחת המטריצות או (במקרה הראשון המרכז שייך לציר , ובשני המרכז אינו שייך לציר ). חבורות הקולינאציה הן ו-, בהתאמה.
ישר במישור פרויקטיבי נקרא ישר הזזה אם יש חבורת סימטריות של המישור המייצבת את כל הנקודות ב-, ופועלת רגולרית על הנקודות מחוץ ל-. מישור שכל הישרים שלו הם ישרי הזזה נקרא מישור Moufang.
מישורים פרויקטיביים סופיים[עריכת קוד מקור | עריכה]
 ערך מורחב – מישור פרויקטיבי סופי
ערך מורחב – מישור פרויקטיבי סופי
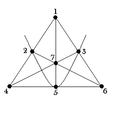
כל מישור פרויקטיבי סופי הוא מערכת שטיינר מן הצורה . למישור פרויקטיבי סופי יש סדר אם על כל ישר יש נקודות. מישור פאנו (באיור משמאל) הוא המישור הפרויקטיבי היחיד מסדר 2. יש מישור מכל סדר שהוא חזקת ראשוני.
קיומם של מישורים פרויקטיביים סופיים מסדרים אחרים היא שאלה פתוחה. ההגבלה הכללית היחידה הידועה על הסדר היא משפט ברוק-רייזר-צ'ולה שאם הסדר N משאיר שארית 1 או 2 בחלוקה ל-4, הוא חייב להיות סכום של שני ריבועים. זה שולל N = 6. המקרה הבא N = 10 נשלל על ידי חישובי מחשב מסיביים. השאלה אם קיים מישור השלכה סופי בסדר N = 12 עדיין פתוחה.
מיון המישורים הפרויקטיביים נעשה בשכבות: ככל שמניחים סימטריות חזקה יותר, כך נעשה המיון מדויק יותר. מתברר שחבורת הסימטריות פועלת על קבוצת הנקודות במישור באופן טרנזיטיבי, 2-טרנזיטיבי או רגולרי (=טרנזיטיבי בחדות) אם ורק אם היא פועלת באותו אופן על אוסף הישרים. אם הפעולה טרנזיטיבית, אפשר לתאר את המישור כקבוצת הפרֶשים בחבורה. אם חבורת הסימטריות פועלת 2-טרנזיטיבית על הנקודות, אז המישור הוא קלאסי, כלומר מוגדר על ידי שדה סופי.
מקורות[עריכת קוד מקור | עריכה]
- Finite flag-transitive projective planes: a survey and some remarks; Koen Thas, Discrete Mathematics 266 (2003), 417--429.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- מישור פרויקטיבי, באתר MathWorld (באנגלית)




![{\displaystyle [x_{1}:x_{2}:x_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6275ad5d46bfd2cd6c176d2b1ff24690840920ef)

![{\displaystyle [1:0:0]=[5:0:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46ec84ee6ce8ae7c5b8130c048e90826271560fb)


















