שפה רגולרית
בתורת השפות הפורמליות, שפה רגולרית היא שפה פורמלית שאפשר לתאר על ידי אוטומט סופי, האמור לקבוע לגבי מילה נתונה אם היא שייכת לשפה אם לאו. משפחת השפות הרגולריות היא המשפחה הראשונה בהיררכיית השפות של חומסקי.
הגדרה[עריכת קוד מקור | עריכה]
אוטומט סופי דטרמיניסטי הוא מערכת הכוללת מספר סופי של מצבים וחוקי מעבר ממצב למצב, התלויים בקלט. אחד המצבים מוגדר כמצב ההתחלה. חלק מהמצבים מוגדרים כמצבים מקבלים. האוטומט מתחיל את הריצה במצב ההתחלה וקורא את אותיות המילה הנתונה בזו אחר זו על פי הסדר. הוא עובר ממצב למצב לאחר קריאת כל אות. בכל שלב, המצב הבא נקבע על ידי המצב הנוכחי של האוטומט והאות הנקראת, על פי חוקי המעבר. הריצה מסתיימת לאחר שהאוטומט גמר לקרוא את כל האותיות במילה. אם בסוף הריצה, האוטומט הגיע לאחד מהמצבים המקבלים, המילה מתקבלת; אחרת, היא נדחית. אוסף המלים שהאוטומט מקבל, (בסימנים, ) נקרא "שפה רגולרית".
את המושג "שפה רגולרית" אפשר להגדיר בדרכים שונות:
- שפה שאפשר לתאר על ידי אוטומט סופי לא דטרמיניסטי, היא שפה רגולרית (משום שאפשר להחליף כל אוטומט כזה באוטומט דטרמיניסטי, גם אם בעל מספר גדול יותר של מצבים).
- כל שפה המתקבלת על ידי דקדוק רגולרי היא רגולרית. (ולהפך, כל שפה רגולרית ניתנת לתיאור על ידי דקדוק רגולרי)
- כל שפה רגולרית ניתנת להגדרה על ידי ביטוי רגולרי. (ולהפך, כל שפה המתוארת על ידי ביטוי רגולרי, רגולרית)
דוגמאות[עריכת קוד מקור | עריכה]
- הדוגמה הפשוטה ביותר לשפה רגולרית היא השפה הריקה. כיוון שכל אוטומט סופי דטרמיניסטי חסר מצבים מקבלים יתאר אותה.
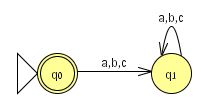
- השפה {}, המכילה את המילה הריקה ותו לא, היא רגולרית, (מעל הא"ב ) מאחר שהאוטומט הבא מקבל אותה (העיגול הכפול מסמן מצב מקבל)
- השפה שהמלים החוקיות שלה הן אלו שבהן האות a מופיעה לפחות שלוש פעמים, מתוארת על ידי האוטומט

לעומת זאת, השפה אינה רגולרית, מאחר שזיהוי מילים בשפה תדרוש מהאוטומט "לספור" מספר לא חסום של אותיות - משימה שאינה אפשרית עבור אוטומט סופי, שזכרונו מוגבל.
תכונות מרכזיות של שפות רגולריות[עריכת קוד מקור | עריכה]
אם ו- שפות רגולריות, אז האיחוד שלהן (השפה הכוללת את כל המלים שהן חוקיות באחת משתיהן) גם הוא שפה רגולרית. גם השרשור (השפה בעלת המלים , לכל ו- ) הוא שפה רגולרית. אם שפה רגולרית, גם השפה הנוצרת על-ידה (שהיא השפה שהמלים שלה מורכבות מקטעים ) היא שפה רגולרית.
הווה אומר, אוסף השפות הרגולריות סגור תחת פעולות האיחוד, השרשור, והיצירה. משפט Kleene (פורסם ב-1956) קובע שכל שפה רגולרית אפשר לקבל מן השפות הסינגלטוניות (שפות הכוללות מילה יחידה באורך 1), על ידי שלוש פעולות אלה. הוכחת המשפט היא קונסטרוקטיבית: ידוע אלגוריתם לבניית אוטומט המתאר שפה על-פי המבנה שלה כאיחוד, שרשור ויצירה מתוך שפות סינגלטוניות, ובכיוון ההפוך, יש אלגוריתם שיכול לתאר את השפה שאוטומט נתון מקבל, כאיחוד, שרשור ויצירה של שפות סינגלטוניות.
בכל אוטומט אפשר להפוך את המצבים המקבלים ללא מקבלים ולהפך, וכך להחליף את השפה שהוא מקבל, בשפה המשלימה (הכוללת את כל המלים שנדחו קודם לכן). מכאן יוצא שאוסף השפות הרגולריות סגור, בנוסף לפעולות שהוזכרו לעיל, גם תחת הפעולות של לקיחת משלים, חיתוך והפרש.
ידוע שלכל שפה רגולרית קיים אוטומט יחיד (עד כדי החלפת שמות המצבים), בעל מספר מצבים מינימלי, המתאר אותה.
משפט חשוב אחר, של Schulzenberger (מ-1965) מתאר את משפחת השפות המתקבלות מן השפות הסינגלטוניות על ידי פעולות האיחוד, השרשור והמשלים: אלו הן כולן שפות רגולריות, המתאפיינות בכך שבאוטומט המינימלי המתאר אותן אין מעגלים (למעט, אולי, לולאות באורך 1). פירושו של דבר הוא שהחבורה למחצה הצמודה לאוטומט מקיימת את הזהות , כאשר n הוא מספר המצבים.
משפט זה מספק גם קשר ללוגיקה מתמטית: השפות המתקבלות מפעולות איחוד, שרשור ומשלים, הן השפות הרגולריות שאפשר לתאר באופן פורמלי במסגרת שפה מסדר ראשון. את כל השפות הרגולריות אפשר לתאר במסגרת שפה מסדר שני. קיומה של שפה כדוגמת , שהיא רגולרית אבל אינה ניתנת לבניה בעזרת איחוד, שרשור ופעולת המשלים, מוכיח שהיכולת התאורית של שפות מסדר שני חזקה מזו של כל השפות מסדר ראשון.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- שמואל זקס ונסים פרנסיז, אוטומטים ושפות פורמליות א, האוניברסיטה הפתוחה, 2000
- שמואל זקס ונסים פרנסיז, אוטומטים ושפות פורמליות ב, האוניברסיטה הפתוחה, 2000
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- אוטומטים סופיים ושפות רגולריות, בבלוג "לא מדויק" של גדי אלכסנדרוביץ', 30 באוגוסט 2009


















