זרימה בצנרת

זרימה בצנרת^[1] הוא ענף במכניקת זורמים אשר דן במשוואות התנועה, פרופילי המהירות והכוחות הפועלים על זורם בלתי דחיס כאשר הוא מבצע תנועה בצינור סגור (לא בתעלה פתוחה).

זרימה בתעלה פתוחה איננה חלק מנושא זה, מכיוון שבתעלה פתוחה חשוף הזורם מצידו העליון ללחץ וטמפרטורת הסביבה.

זרימה בצנרת יכולה להתקיים במספר משטרי זרימה בהתאם למספר ריינולדס של הבעיה.

נושא הפסדי הלחץ בזרימה בא לידי ביטוי בזרימת דם בוורידים ועורקים, במכשור רפואי וכדומה.

משוואת ברנולי – חוק שימור האנרגיה^[1][עריכת קוד מקור | עריכה]

ערך מורחב – משוואת ברנולי

לצורך הבנת המגמות העיקריות בזרימה נתחיל בהזנחת החיכוכים בצנרת (הנחה בלתי סבירה אך שימושית בשלב זה).

בהזנחת החיכוך ניתן להניח שהאנרגיה של הזורם נשמרת בזמן תנועתו בצינור. על פי משוואת ברנולי: $P+\rho gh+{\frac {1}{2}}\rho {{v}^{2}}=const$

על פי משוואה זו ניתן לראות כי אם לא יהיו שינוי גובה בזרימה ו/או שינוי שטח החתך של הצינור אזי גם הלחץ יישמר לאורך הצינור.

לעומת זאת, שינוי כלשהו בגובה או בשטח החתך יחייב הפרשי לחצים בתוך הצינור:

דוגמה א': הצרת שטח החתך תגרום לעליית המהירות (נובע ישירות משימור מסה) ולפיכך הלחץ ירד בהכרח. דבר אשר יוצר הפרש לחצים בצינור.
דוגמה ב': עלייה אנכית בגובה הצינור h (עיקול צנרת כלפי מעלה) יגרום לירידת הלחץ, דבר היוצר, גם כן, הפרש לחצים בצינור.

בפועל, אפקטי החיכוך הם גורם משפיע מאוד והטיפול בהם יפורט לאורך הפרק הנוכחי.

משטר הזרימה בצנרת:^[1][עריכת קוד מקור | עריכה]

למעט זורמים צמיגים מאוד, לרוב הזרימה בצנרת היא טורבולנטית לחלוטין. המשטר ייקבע מתוך ערכו של מספר ריינולדס (מסומן Re, גודל חסר ממד אשר מייצג את היחס בין אינרציית הזורם וצמיגותו). מספר ריינולדס גבוה מעיד על זרימה בה האינרצייה שולטת בבעיה ומספר ריינולדס קטן מעיד על זרימה בה הצמיגות שולטת בבעיה.

בזרימה בצנרת:

$\operatorname {Re} \leq 2300$ - זרימה למינארית
$2300<\operatorname {Re} <4000$ - אזור מעבר בין זרימה למינארית לטורבולנטית.
$\operatorname {Re} \geq 4000$ - זרימה טורבולנטית

כאשר: $\operatorname {Re} ={\frac {\rho UD}{\mu }}={\frac {UD}{\nu }}$

זרימה למינרית מפותחת בצינור עגול^[1][עריכת קוד מקור | עריכה]

זרימה למינרית בצינור תתקיים עבור: $\operatorname {Re} \leq 2300$ והיא זרימה המונעת על ידי מפל לחצים מסוג זרימת פואסיל.

באיור מספר 2 בוצע מאזן כוחות על נפח בקרה אינפטיסימלי בזורם. סכום הכוחות הפועלים על הנפח בכיוון x חייב להתאפס כי הרי הזורם איננו מאיץ (הוא בשיווי משקל כי הזרימה מפותחת).

לאחר חלוקה ב $2\pi r$ מתקבל: ${\frac {\partial p}{\partial x}}={\frac {{\tau }_{rx}}{r}}+{\frac {d{{\tau }_{rx}}}{dr}}={\frac {1}{r}}\cdot {\frac {d\left(r{{\tau }_{rx}}\right)}{dr}}$

מאמץ הגזירה מוגדר להיות: ${{\tau }_{rx}}=\mu {\frac {\partial u}{\partial r}}$

ופתרון המשוואה הדפרנציאלית הואו: $\mu {\frac {du}{dr}}={{\tau }_{rx}}={\frac {r}{2}}\left({\frac {\partial p}{\partial x}}\right)+{\frac {{c}_{1}}{r}}$

מכיוון שמאמץ גזירה איסופי לא ייתכן, אזי $C_{1}=0$ ומכאן נקבל ביטוי למאמץ הגזירה: ${{\tau }_{rx}}={\frac {r}{2}}\left({\frac {\partial p}{\partial x}}\right)$

ולכן, על פי החוק השלישי של ניוטון, הגזירה שמפעילה הדופן על הזורם היא: ${{\tau }_{w}}=-{\frac {R}{2}}\left[{\frac {\partial p}{\partial x}}\right]$

זרימה טורבולנטית מפותחת בצינור עגול[עריכת קוד מקור | עריכה]

ערך מורחב – זרימה טורבולנטית

^[1]

זרימה טורבולנטית תתקיים עבור: $\operatorname {Re} \geq 4000$

בזרימה למינארית מאמצי הגזירה פרופורציונליים לצמיגות ולגרדיאנט המהירות. בזרימה טורבולנטית, מנגד, נוצרות מערבולות אשר פועלות על מנת להקטין את גרדיאנטי המהירות.

ניתן לחלק את המערבולות הללו למהירויות ממוצעות (לכן בנוסחה מופיע קו מעליהן) בזמן בכיוון x ובכיוון r .הפחתה זו של מאמץ הגזירה קיבלה את השם "מאמצי ריינולדס".

לכן, מאמצי הגזירה בזרימה טורבולנטית מפותחת הם: ${{\tau }_{rx}}=\mu {\frac {\partial u}{\partial x}}-\rho {\overline {{{u}_{x}}{{u}_{r}}}}$

מתוך ניסויים שנעשו במספרי ריינולדס שונים, התגלה כי תופעה זו מתאפסת בסמוך לדפנות הצינור. לכן על הדופן, על אף שהזרימה טורבולנטית: ${{\tau }_{rx}}=\mu {\frac {\partial u}{\partial r}}$ .

התופעה אינה זניחה בשכבות פנימיות בצינור.

קוטר אפקטיבי (הקוטר ההידראולי)^[1][עריכת קוד מקור | עריכה]

מכיוון שלרוב היישומים ההנדסיים משתמשים בצינורות עגולים, הניתוח יעשה בקואורדינטות גליליות ובחתך עגול. הפתרונות המתקבלים נכונים גם לצינורות מרובעים ומשולשים תחת הדרישה הבאה: ${\frac {height}{width}}\leq 4$ . כלומר, יחס גובה לרוחב לא גדול מ-4.

עבור כל צינור ניתן לחשב קוטר הידראולי: ${{D}_{h}}={\frac {4\cdot Area}{Perimeter}}$ . קוטר זה ישמש בתפקיד הקוטר בכל החישובים בהמשך.

החיכוך בצנרת[עריכת קוד מקור | עריכה]

^[1]

החיכוך הוא מנגנון של הפסד אנרגיה, כלומר אנרגיית הזורם יורדת ככל שהוא מתקדם לאורך הצינור ומושפע מהחיכוך עם דפנות הצינור.

החיכוכים בצנרת יחולקו לשני סוגים עיקריים:

הפסדים ראשיים – הפסדים הנובעים מזרימה מפותחת של הזורם לאורך הצנרת כאשר שטח החתך אחיד.
הפסדים משניים – הפסדים הנובעים מתנועת הזורם בשסתומים, פניות חדות ומהכניסה לצינור.

החלוקה תהיה נכונה רק עבור צנרת שרובה המכריע עשוי מצינורות אופקיים ללא שינוי שטח חתך, פניות, פיצולים ושסתומים.

בעזרת משוואת ברנולי ניתן לתאר את הפסדי החיכוך כך: $\left({\frac {{p}_{1}}{\rho }}+{{\alpha }_{1}}{\frac {{{\bar {V}}_{1}}^{2}}{2}}+g{{z}_{1}}\right)-\left({\frac {{p}_{2}}{\rho }}+{{\alpha }_{2}}{\frac {{{\bar {V}}_{2}}^{2}}{2}}+g{{z}_{2}}\right)={{h}_{{l}_{T}}}$

כאשר המהירויות שוות ותכונות הזורם נשארות קבועות ניתן לקבל את התוצאה המופשטת: ${\frac {{{p}_{1}}-{{p}_{2}}}{\rho }}=g({{z}_{2}}-{{z}_{1}})+{{h}_{l}}$

בנוסף, אם הצינור אופקי, אזי הגובה איננו משתנה ונקבל: ${\frac {{{p}_{1}}-{{p}_{2}}}{\rho }}={\frac {\Delta p}{\rho }}={{h}_{l}}$

הפסדים ראשיים – הנובעים מזרימה מתמדת בצינור אופקי ללא שינוי שטח החתך[עריכת קוד מקור | עריכה]

הפסדי לחץ הנובעים מחיכוך בזרימה למינרית[עריכת קוד מקור | עריכה]

^[2]^[1]

בזרימה למינרית, מכיוון ש ${\frac {\partial p}{\partial x}}=const={\frac {\Delta p}{\Delta x}}$ .

ניתן לתאר את הפסדי הלחץ בצורה פשוטה יחסית: $\Delta p=32{\frac {L}{D}}\cdot {\frac {\mu {\bar {V}}}{D}}$

ולכן: ${{h}_{l}}={\frac {\Delta p}{\rho }}=\left({\frac {64}{\operatorname {Re} }}\right){\frac {L}{D}}{\frac {{\bar {V}}^{2}}{2}}$ .

הפסדי לחץ הנובעים מחיכוך בזרימה טורבולנטית[עריכת קוד מקור | עריכה]

בזרימה טורבולנטית לא נוכל לקבל ביטוי אנליטי פשוט להפסדי הלחץ, אך על ידי ניסויים ואנליזה ממדית (אנליזה למציאת הגורמים השולטים והזניחים בבעיה הנדסית) נוכל לקבל קירוב טוב.

נתחיל בהגדרת הפרמטרים בהם תלוי הפסד הלחץ:

$\Delta p=f\left(L(length),D(diameter),e(roughness),\mu (viscosity),{\bar {V}}(average{\text{ }}velocity),\rho (density)\right)$

מאנליזה ממדית על פי עקרון $\pi$ של בקינגהם נקבל: $\left.{\begin{aligned}&{\frac {\Delta p}{\rho {{\bar {V}}^{2}}}}=f\left({\frac {\mu }{\rho {\bar {V}}D}},{\frac {L}{D}},{\frac {e}{D}}\right)\\&{\frac {\Delta p}{\rho {{\bar {V}}^{2}}D}}=\phi \left(\operatorname {Re} ,{\frac {L}{D}},{\frac {e}{D}}\right)\\&{\frac {{h}_{l}}{{\bar {V}}^{2}}}=\phi \left(\operatorname {Re} ,{\frac {L}{D}},{\frac {e}{D}}\right)\\&{\frac {{h}_{l}}{{\frac {1}{2}}{{\bar {V}}^{2}}}}=\phi \left(\operatorname {Re} ,{\frac {L}{D}},{\frac {e}{D}}\right)\\\end{aligned}}\right\}$

כעת הביטוי כתוב כיחס בין "הפסדי אנרגיה בצורת לחץ" ובין "האנרגיה הקינטית" של הזורם.

מניסויים עולה כי ההפסדים תלויים בצורה ישירה ליחס בין אורך הצינור וקוטרו ולכן נרשום: ${\frac {{h}_{l}}{{\frac {1}{2}}{{\bar {V}}^{2}}}}={\frac {L}{D}}\phi \left(\operatorname {Re} ,{\frac {e}{D}}\right)$

הפונקציה הנעלמת כאן מוגדרת כ"מקדם החיכוך" ותסומן כך: $f=\phi \left(\operatorname {Re} ,{\frac {e}{D}}\right)$ .

ולסיכום נרשום ביטוי פשוט יחסית: ${{h}_{l}}=f\cdot {\frac {L}{D}}\cdot {\frac {{\bar {V}}^{2}}{2}}$

את המקדם $f$ נמצא מתוך דיאגרמה אמפירית בשם: "דיאגרמת מודי". דיאגרמה זו (המופיעה באיור 3) היא בעצם, שרטוט הפונקציה $f$ עבור ערכי Re שונים כאשר $e/D$ ידוע.

לכן, על מנת להשתמש בה עלינו לחשב את ערכו של $e$ שאיננו ידוע עדיין.

את ערך $e$ נחשב מתוך טבלה מספר 1:

טבלה מספר 1 - Roughness^[1]

 $e[mm]$

Pipe Type

0.9 - 9

Riveted Steel

0.3 - 3

Concrete

0.2 - 0.9

Wood Stave

0.26

Cast Iron

0.15

Galvanized Iron

0.046

Commercial Steel or Wrought Iron

0.0015

Drawn Tubing

בשימוש ב"דיאגרמת Moody" יש צורך במספר ריינולדס אותו נחשב, כאמור, ע"י: $\operatorname {Re} ={\frac {\rho UD}{\mu }}={\frac {UD}{\nu }}$ .

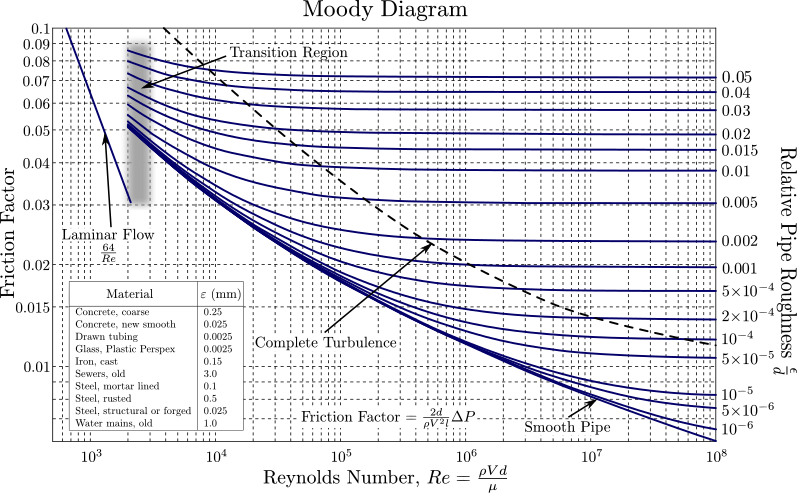
באזור הלמינארי ההפסדים הם: ${{h}_{l}}=\left({\frac {64}{\operatorname {Re} }}\right){\frac {L}{D}}{\frac {{\bar {V}}^{2}}{2}}$ . לכן, לפי הגדרת מקדם החיכוך נקבל כי כאשר הזרימה למינארית ערכו של $f$ פרופורציוני הפוך ל $Re$ בלבד וערכו: $f={\frac {64}{\operatorname {Re} }}$ .

השימוש בדיאגרמה פשוט ובכל זאת בוצעו ניסיונות רבים לתרגם את הדיאגרמה למשוואה שתייתר את השימוש בדיאגרמה.

Colebrook - משוואה סתומה (לא מפורשת ב- $f$ ) : ${\frac {1}{{f}^{0.5}}}=-2.01\cdot \log \left({\frac {e}{3.7\cdot D}}+{\frac {2.51}{\operatorname {Re} {{f}^{0.5}}}}\right)$ . המשוואה ניתנת לפתרון בפשטות בכל תוכנת חישוב בסיסית או על ידי איטרציות או על ידי פונקציית W של למברט(אנ').
Miller - הציע את הניחוש ההתחלתי למשוואה האיטרטיבית בעזרתו נקבל דיוק של אחוז בודד אחרי איטרציה בודדת בלבד. ${{f}_{o}}=0.25{{\left[\log \left({\frac {e}{3.7\cdot D}}+{\frac {5.74}{{\operatorname {Re} }^{0.9}}}\right)\right]}^{-2}}$
Blausius - הציע ביטוי למקדם החיכוך לזרימות טורבולנטיות בצינורות חלקים תחת התנאי $\operatorname {Re} \leq {{10}^{5}}$ : $f={\frac {0.316}{{\operatorname {Re} }^{0.25}}}$

על ידי שימוש ב: ביטוי זה של Blausius, הגדרת מקדם החיכוך ובביטוי לגזירה בדופן נוכל לקבל ביטוי פשוט למאמץ הגזירה בדופן הצינור: ${{\tau }_{w}}=0.0332\rho {{\bar {V}}^{2}}{{\left({\frac {\nu }{R{\bar {V}}}}\right)}^{0.25}}$

הפסדים משניים – נובעים משינוי שטח החתך, פניות, שינויי גובה וכדומה^[2]^[1][עריכת קוד מקור | עריכה]

באופן כללי מחושבים ההפסדים בצורה הבאה, כאשר הקבוע $\mathrm {K}$ נקבע בצורה שונה עבור כל סיטואציה: ${{h}_{{l}_{m}}}=\kappa {\frac {{\bar {V}}^{2}}{2}}$

כניסות ויציאות[עריכת קוד מקור | עריכה]

תכנון לקוי של הכניסה לצנרת, לדוגמה: פינות חדות אשר יאלצו את הזרימה להתנתק ולהאיץ, עלול לגרום להפסדי לחץ ניכרים.

ברור כי ככל שהפינות תהיינה מעוגלות יותר כך ההפסדים יקטנו. במידה ובכניסה הפינות תהיינה מעוגלת היטב $\left({\frac {r}{D}}\geq 0.15\right)$ ההפסד בכניסה יהיה זניח לחלוטין.

ערכו של $\mathrm {K}$ נקבע בניסויים עבור כל כניסה אך ככלל אצבע נשתמש במקדמים הבאים: (באיור 4^[1]):

שינויים חדים בשטח החתך[עריכת קוד מקור | עריכה]

שינויים בשטח החתך מאלצים את הזרימה לשנות את מהירותה על מנת לקיים שימור מסה. הדבר גורם להפסדי לחץ. נגדיר יחס שטחי חתך כך: $AR={\frac {{A}_{small}}{{A}_{big}}}$ . מקדם זה נע בתחום $0\leq AR\leq 1$ .

בעזרת הגרף (איור 5^[1]) נחשב את $\mathrm {K}$ בצורה דומה הן להצרה והן להרחבת שטח החתך.

שינויים מתונים בשטח החתך[עריכת קוד מקור | עריכה]

נשתמש בטבלה 2 אשר תגדיר את $\mathrm {K}$ עבור ערכי AR וזווית פתיחה שונים. הגאומטריה הרלוונטית מופיעה באיור מספר 6.

טבלה 2 - מקדם $\mathrm {K}$ לשינוי מתון בשטח החתך^[1]
Included Angle $\theta$ , Degrees
150	120	90	50-60	15-40	10	$A2/A1$
0.24	0.18	0.12	0.06	0.05	0.05	0.50
0.35	0.27	0.17	0.07	0.04	0.05	0.25
0.37	0.29	0.19	0.08	0.05	0.05	0.10

כיפופים בצינור[עריכת קוד מקור | עריכה]

על פניו, נרצה לומר שהפסדי חיכוך בצינור מעוקל דומים לאלו של צינור ישר כל עוד נלקח אורכו המלא של העיקול. בפועל, נוצרת בעיקול זרימה משנית אשר גורמת להפסדים נוספים. לכן נמצא אורך שקול מנורמל $L_{e}/D$ מתוך דיאגרמות מבוססות ניסויים ונציבו לנוסחה שקיבלנו להפסדים ראשיים: ${{h}_{l}}=f\cdot {\frac {{L}_{eq}}{D}}\cdot {\frac {{\bar {V}}^{2}}{2}}$

עבור כיפוף רציף של 90 מעלות ברדיוסים שונים האורך השקול המנורמל ייקבע על ידי איור 6^[1]:

עבור פניות חדות בזוויות שונות האורך השקול המנורמל $L_{e}/D$ ייקבע על ידי איור 7^[1]:

שסתומים ואביזרים[עריכת קוד מקור | עריכה]

שסתומים סגורים מהווים מחסום עבור הזורם. בבואנו לחשב הפסדים הנובעים מחיכוך נחשב אותם עם שסתום פתוח לרווחה. שוב נשתמש בנוסחה שקיבלנו להפסדים ראשיים : ${{h}_{l}}=f\cdot {\frac {{L}_{eq}}{D}}\cdot {\frac {{\bar {V}}^{2}}{2}}$

כאשר את האורך השקול המנורמל $L_{e}/D$ נוציא מטבלה מספר 3 או מקטלוג יצרן.

^[1]**טבלה 3 - אורך שקול מנורמל לחישוב הפסדי לחץ באביזרים שונים**
$L_{e}/D$ Equivalent Legth	Fitting Type
	Valves
8	Gate Valve
340	Globe Valve
150	Angle Valve
3	Ball Valve
600	Globe Lift Check Valve
55	Angle Lift Check Valve
30	Standart Elbow 90°
16	Standart Elbow 45°
50	Return Bend, Close Pattern

מקורות[עריכת קוד מקור | עריכה]

Fox, Robert W., and Alan T. Mcdonald. Introduction to Fluid Mechanics. 6th ed. N.p.: John Wilet & Sons, 2004
https://web.archive.org/web/20150218120914/http://www.efm.leeds.ac.uk/CIVE/CIVE1400/PDF/Notes/section_all2.pdf - An Introduction to Fluid Mechanics School of Civil Engineering, University of Leeds
http://www.codecogs.com/library/engineering/fluid_mechanics/pipes/head_loss/index.php - calculator for head loss

הערות שוליים[עריכת קוד מקור | עריכה]

^ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ ¹⁴ ¹⁵ ¹⁶ Fox, Robert W., and Alan T. Mcdonald, Introduction to Fluid Mechanics. 6th ed.:, John Wilet & Sons, 2004
^ ¹ ² code coges

[:1-1] ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ ¹⁴ ¹⁵ ¹⁶ Fox, Robert W., and Alan T. Mcdonald, Introduction to Fluid Mechanics. 6th ed.:, John Wilet & Sons, 2004

[:2-2] ¹ ² code coges

[1]

[2]

משוואת ברנולי – חוק שימור האנרגיה[1][עריכת קוד מקור | עריכה]

משטר הזרימה בצנרת:[1][עריכת קוד מקור | עריכה]

זרימה למינרית מפותחת בצינור עגול[1][עריכת קוד מקור | עריכה]