מישור פרויקטיבי סופי

בקומבינטוריקה, מישור פרויקטיבי סופי הוא מישור פרויקטיבי בעל מספר סופי של נקודות (זה שקול לכך שקבוצת הישרים סופית, וגם לכך שעל אחד הישרים יש מספר סופי של נקודות). כל מישור פרויקטיבי סופי הוא מערכת שטיינר מן הצורה $S(2,n+1,n^{2}+n+1)$.

בניגוד למקרה האינסופי, שבו המקרה המעניין ביותר הוא המישור הקלאסי המוגדר מעל שדה, במקרה הסופי יש עניין רב גם במישורים שאינם כאלה.

הסדר של מישור פרויקטיבי

במישור פרויקטיבי נתון, יש על כל ישר אותו מספר נקודות, וזה גם מספר הישרים העוברים דרך כל נקודה. למעשה, אם על ישר יש $n+1$ נקודות, אז מספר הנקודות במישור הוא $\ n^{2}+n+1$. מישור כזה הוא מסדר n.

את ההתאמה בין שני ישרים אפשר לראות באופן הבא.

• נניח שעל הישר $l$ נמצאות בדיוק $n+1$ נקודות. לכל ישר $l'\neq \ l$ אפשר לבחור נקודה $\ Q$ שאינה על שני הישרים, ולהגדיר העתקה מ-$l$ ל-$l'$ על ידי חיתוך הישר העובר דרך $Q$ ו-$p_{i}$ כלשהי, עם הישר $l'$. העתקה כזו היא הפיכה, ולכן מספר הנקודות על $l$ ועל $l'$ שווה. מכאן רואים, שבכל ישר במרחב ישנו אותו המספר של נקודות.
• בהינתן נקודה $P$ וישר $l$ שאינו עובר דרכה, כל נקודה $Q\in \ l$ משרה ישר יחיד העובר דרך $P$ ו-$Q$. מכאן שמספר הנקודות על $l$ שווה למספר הישרים העוברים דרך $P$. בפרט, דרך כל הנקודות במרחב עובר אותו מספר ישרים.
• נבחן את מספר הנקודות במרחב פרויקטיבי כלשהו מעל שדה סופי. נסמן ב-$n+1$ את מספר הנקודות הנמצאות על כל ישר (שהוא גם מספר הישרים העובר דרך נקודה כלשהי). נבחר נקודה $P$ כלשהי ונצייר את כל הישרים העוברים דרכה - ישנם $n+1$ כאלו. כאמור, בכל ישר כזה ישנן $n+1$ נקודות. מכיוון של-$n$ הישרים ישנה נקודה המשותפת לכולם, היא $P$, נקבל סה"כ $\ n^{2}+n+1$ נקודות. מכיוון שדרך כל נקודה במישור עובר ישר החותך את $\ P$, קבלנו שזהו מספר הנקודות במישור.
• שיקול דומה יראה כי מספר הישרים במישור שוה למספר הנקודות במישור.

המישור הפרויקטיבי מסדר 2

מישור פאנו (אינו ניתן לשיכון במישור האוקלידי)

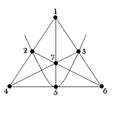
במישור הפרויקטיבי הקטן ביותר יש $2^{2}+2+1=7$ נקודות. יש רק מישור אחד כזה - מישור פאנו (ע"ש המתמטיקאי ג'ינו פאנו), המתואר בציור שמשמאל.

סדרים אפשריים

המישור הקלאסי מעל שדה סופי מספק מישור פרויקטיבי מסדר $n$, לכל $n$ שהוא חזקת-ראשוני (לכל סדר כזה יש מישור קלאסי אחד, משום שכל השדות מאותו סדר איזומורפיים). עד לסדר 8, זוהי הבנייה היחידה למישור פרויקטיבי; אבל יש 4 מישורים שונים מסדר 9, ולפחות 22 מסדר 16. משערים שהסדר של כל מישור פרויקטיבי הוא חזקת ראשוני. לפי משפט Bruck-Ryser, אם $n$ שקול ל-1 או ל-2 מודולו 4, אז n הוא סכום של שני ריבועים. בפרט, אין מישורים פרויקטיביים מסדר 6 או 14. הוכחה מפרכת באמצעות מחשב הראתה שגם מישורים מסדר 10 אינם קיימים. המקרה הפתוח הראשון הוא של מישורים מסדר 12.

השקילות למערכת אורתוגונלית של ריבועים לטיניים

זוג ריבועים לטיניים $(a_{ij}),(b_{ij})$, בגודל $n$-על-$n$, הם אורתוגונליים, אם הזוגות $(a_{ij},b_{ij})$ שונים זה מזה. נראה שמישור פרויקטיבי שקול למערכת של $n-1$ ריבועים לטיניים בגודל $n$-על-$n$ שהם אורתוגונליים בזוגות. כלומר, קיים מישור פרויקטיבי מסדר $n$ אם ורק אם קיימים $n-1$ ריבועים לטיניים מאונכים בזוגות מסדר $n$.

נניח שנתונה מערכת כזו של ריבועים לטיניים. הנקודות תהיינה המשבצות בלוח $n$-על-$n$, הריבועים הנתונים, וכן "נקודת השורות" ו"נקודת העמודות". עבור כל ריבוע לטיני, וכל ערך שמופיע בו, נגדיר "ישר" שיכלול את כל הנקודות שמייצגות את המשבצות בהן מופיע הערך, וכן את הנקודה שמייצגת את אותו ריבוע לטיני. עבור כל שורה או עמודה בלוח הריבועי, נגדיר "ישר" של כל המשבצות בה, ונקודת השורות או נקודת העמודות, בהתאמה. לסיום נגדיר "ישר" אחרון, שיכלול את כל הנקודות שמייצגות ריבועים לטיניים, יחד עם נקודת השורות ונקודת העמודות. קל לראות שנקודות וישרים אלה מהווים מישור פרויקטיבי סופי מסדר $n$.

מישורים סימטריים

מיון המישורים הפרויקטיביים נעשה בשכבות: ככל שמניחים סימטריות חזקה יותר, כך נעשה המיון מדויק יותר. מתברר שחבורת הסימטריות פועלת על קבוצת הנקודות במישור באופן טרנזיטיבי, 2-טרנזיטיבי או רגולרי (=טרנזיטיבי בחדות) אם ורק אם היא פועלת באותו אופן על אוסף הישרים. נסמן $N=n^{2}+n+1$.

תיאור לפי קבוצות הפרֶשים

יש משפחה רחבה של מישורים פרויקטיביים הנמצאים בהתאמה לקבוצות הפרשים של חבורות. קבוצה $D$ של איברים בחבורה $G$ נקראת קבוצת הפרֶשים אם כל איבר בחבורה אפשר להציג באופן יחיד כמנה $\ xy^{-1}$ עבור $\ x,y\in D$. כל חבורה $G$ (מסדר > 3) עם קבוצת הפרשים $D$ מגדירה מישור פרויקטיבי באופן הבא: הנקודות והישרים נמצאים בהתאמה לאברי $G$, והנקודה המתאימה ל-$a$ נמצאת על הישר המתאים ל-$b$, אם ורק אם $ab^{-1}\in D$. מן הבניה יוצא ש-$G$ פועלת רגולרית על הנקודות (והישרים) של המישור הזה. בכיוון ההפוך, אם $G$ פועלת רגולרית על הנקודות במישור $P$ (חבורה כזו נקראת חבורת זינגר), אז לכל נקודה $p$ וישר $\ \ell$, $\{g\in G:g(p)\in \ell \}$ מהווה קבוצת הפרשים של $G$; המישור המתאים לקבוצת ההפרשים הזו איזומורפי ל-$P$.

פעולה פרימיטיבית על הנקודות

נניח ש-$P$ הוא מישור לא קלאסי מסדר $n$, שיש חבורה $G$ הפועלת פרימיטיבית על הנקודות שלו. אז $n$ זוגי, $N$ ראשוני, וסדר החבורה מחלק את $nN$ או את $(n+1)N$.

פעולה טרנזיטיבית על הדגלים

נניח ש-$P$ הוא מישור לא קלאסי מסדר $n$, שיש חבורה $G$ הפועלת טרנזיטיבית על הדגלים שלו (דגל הוא זוג הכולל נקודה וישר העובר דרכה). זהו מקרה פרטי של המקרה הקודם, משום שכל חבורה הפועלת טרנזיטיבית על הדגלים פועלת פרימיטיבית על הנקודות. אז $n$ מתחלק ב-8 אבל אינו חזקה של 2, ו-$N$ ראשוני. נוסף לזה, פעולת $G$ על הדגלים היא חדה (לכן היא מסדר $(n+1)N$), ובפעולתה על הנקודות $G$ היא חבורת פרובניוס והיא מכילה תת-חבורה נורמלית (ציקלית) מסדר $N$ שפעולתה על הנקודות רגולרית. כך אפשר לתאר מישור כזה באמצעות קבוצת הפרשים, כפי שהוסבר לעיל.

פעולה 2-טרנזיטיבית על הנקודות

פעולה 2-טרנזיטיבית על הנקודות היא טרנזיטיבית על הדגלים. ההנחה שקיימת פעולה כזו היא חזקה ביותר: אם יש חבורה הפועלת 2-טרנזיטיבית על הנקודות, אז המישור הוא קלאסי (זוהי תוצאה של משפט דומה על מישורים אפיניים, בצירוף העובדה שכל מישור Moufang סופי הוא קלאסי). ואכן, חבורת הסימטריות של המישור הקלאסי פועלת על הנקודות באופן 2-טרנזיטיבי (פעולה 3-טרנזיטיבית אינה אפשרית משום ששלוש נקודות על ישר אחד מוכרחות להישאר על ישר אחד).