משתמש:אור ונעמי/נעמי

תמונה

pushout

pushout

שאלות

1. מוטיבציה של מורפיזם נאות: להבין בדיוק את ההקבלה לטופולוגיה
2. ישר עם שני אפסים - איך בדיוק זה נראה
3. הצגת מרחב פרוייקטיבי כהדבקה

מורפזים מופרד

מוטיבציה

המוטיבציה להגדרה היא הטענה הבאה:

מרחב טופולוגי $X$ הוא האוסדורף אם ורק אם העתקת האלכסון $\Delta :X\to X\times X$ היא העתקה סגורה.

המושג 'סכמה פרידה' אנלוגי למושג 'מרחב טופולוגי האוסדורף', והמושג מורפיזם פריד הוא המושג המתאים בגרסה היחסית.

מורפיזם נאות

מוטיבציה

בקטגוריה של מרחבים טופולוגיים (שבה כל מורפיזם הוא פונקציה רציפה) תת-מרחב קומפקטי עובר למרחב קומפקטי. הצד השני לא בהכרח מתקיים, אבל העתקה $f$ שמקיימת את הצד השני (תמונה הפוכה של תת-מרחב קומפקטי היא קומפקטית) נקראת העתקה נאותה. נאותות של מורפיזמים של סכמות היא תכונה אנלוגית. לדוגמה, יריעות נאותות (proper varieties) מעל $\mathbb {C}$ יהיו יריעות קומפקטיות כשמסתכלים בטופולגיה הרגילה של $\mathbb {C}$.

המוטיבציה להגדרה היא הטענה הבאה:

תהי $C$ הקטגוריה של מרחבי האוסדורף קומפקטיים מקומית בעלי בסיס בן מנייה לטופולוגיה. אז ההעתקה $f:X\to Y$ בקטגוריה $C$ היא סגורה אוניברסלית אם ורק אם היא העתקה נאותה (לכל תת-מרחב קומפקי $V\subseteq Y$ התמונה ההפוכה $f^{-1}(V)$ היא קומפקטית).

מוטיבציה נוספת להגדרה היא העובדה שמורפיזמים פרויקטיבים הם נאותים. מורפיזמים פרויקטיבים הם מורפיזמים מרכזיים ביותר בגאומטריה אלגברית, ואפשר לראות בנאותות תכונה נחמדה שהם מקיימים. אפשר אף להסתכל על מורפזמים נאותים כהרחבה של מורפיזמים פרויקטיבים.

טענות

בטענות הבאות נניח כי כל הסכמות נתריות.

• שיכון סגור הוא נאות.
• הרכבה של מורפיזמים נאותים היא מורפיזם נאות.
• מורפיזמים נאותים יציבים תחת הרחבת בסיס.
• אם $f:X\to Y,f':X'\to Y'$ מורפיזמים נאותים של סכמות מעל סכמת בסיס $S$, אז מורפיזם המכפלה $f\times f':X\times _{S}X'\to Y\times _{S}Y'$ גם הוא נאות.
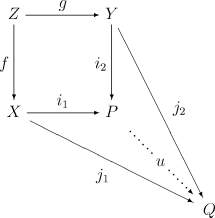
• אם $f:X\to Y,g:Y\to Z$ מורפיזמים כך ש-$g\circ f$ נאות, אזי $f$ נאות.
• מורפיזם $f:X\to Y$ נאות אם"ם $Y$ ניתן לכיסוי ע"י תת קבוצות פתוחות $V_{i}$ כך ש-$f^{-1}(V_{i})\to V_{i}$ נאות לכל $i$.

דוגמאות סכמה:

• כל סכמה אפינית היא סכמה (אנחנו מניחים כי כל החוגים הם קומוטטיביים).
• ${\text{Spec}}\mathbb {Z}$ הוא דוגמה חשובה שהרבה מתורת המספרים הוא מחקר שלה.
• יהי $k$ שדה. פולינום $f\in k[x_{1},..,x_{n}]$ מגדיר תת-סכמה סגורה במרחב האפיני $\mathbb {A} _{k}^{n}$: ${\text{Spec}}(k[x_{1},...,x_{n}]/(f))$. סכמה כזאת נקראת גם היפר יריעה. לדוגמה, הפולינום $f=x^{2}-y^{2}(y+1)$ מגדיר עקומה סינגולרית ב-$\mathbb {A} _{\mathbb {C} }^{2}$.
• עד כאן ערכתי
• לכל חוג $R$ אפשר לבנות את המרחב הפרויקטיבי ה-n ממדי מעל $R$ על ידי "הדבקת" n+1 עותקים של המרחב ${\text{Spec}}(R[x_{1},...,x_{n}])$ לאורך הקבוצות הפתוחות.
• הישר עם "שני" אפסים, ניקח שני עותקים של הישר האפיני (מעל שדה $k$ כלשהו) ונזהה את הנקודות בקבוצה הפתוחה $\mathbb {A} _{\mathbb {C} }^{1}-\{{\bar {0}}\}$ עם עצמן על ידי הזהות, פורמלית: $\left(\mathbb {A} _{\mathbb {C} }^{1}\coprod \mathbb {A} _{\mathbb {C} }^{1}\right)/\sim$ כאשר היחס שקילות הוא זה שתיארנו. זוהי דוגמה לסכמה לא פרידה, ובפרט לא אפינית.
• בהינתן פולינום הומוגני ממעלה חיובית ב-$R[x_{1},...,x_{n}]$ מגדיר תת-סכמה סגורה על ידי $f=0$ במרחב הפרויקטיבי $\mathbb {P} _{R}^{n}$ שנקרא היפר-יריעה פרויקטיבית, פורמלית, תת-הסכמה היא ${\text{Proj}}(R[x_{1},...x_{n}]/f(x))$. לדוגמה, תת-הסכמה המוגדרת על ידי $x^{3}+y^{3}=z^{3}$, זו עקומה אליפטית מעל הרציונלים.
• סיבה טובה להתעניין בסכמות ולא רק בסכמות אפיניות היא שקבוצה פתוחה של סכמה אפינית לא בהכרח תהיה אפינית. לדוגמה, $X=\mathbb {A} ^{n}-0$ למשל מעל המרוכבים; אז המרחב $X$ לא אפיני עבור $n\geq 2$ (עבור $n=1$ נקבל את הציר בלי הראשית וזה איזומורפי ל-${\text{Spec}}\mathbb {C} [x,x^{-1}]$ ובפרט לא אפיני.) כדי להראות שהמרחב שלנו לא אפיני, צריך להראות שכל פונקציה רגולרית על המרחב שלנו נוכל להרחיב על כל המרחב האפיני עבור $n\geq 2$ (הטענה דומה ללמה של הארטוגס מאנליזה מרוכבת אך קלה יותר להוכחה). ההכלה $i:X\to \mathbb {A} ^{n}$ משרה הומומורפיזם של חוגים $i^{\sharp }:{\mathcal {O}}_{\mathbb {A} ^{n}}(\mathbb {A} ^{n})\to {\mathcal {O}}_{X}(X)$. אם $X$ הייתה סכמה אפינית אז i הייתה מורפיזם של סכמות אך היא לא על ולכן לא איזומורפיזם.