פוליאומינו
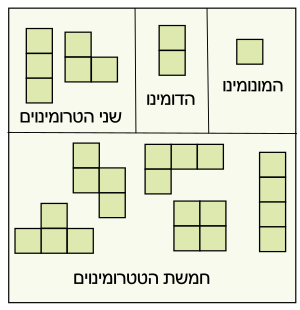

פוליאומינו (Polyomino) הוא אובייקט קומבינטורי המורכב מריבועים המחוברים זה לזה על ידי הצמדת צלעותיהם. האובייקט הוא הכללה של הדומינו, המורכב משני ריבועים המחוברים זה לזה, ומכאן שמו (פולי - רבים). דוגמה בולטת לאבני פוליאומינו הן אבני הטטריס, שמורכבות מארבעה ריבועים כל אחת. עיקר העיסוק בפוליאומינו הוא כשעשוע מתמטי ומקור לחידות, אך קיימות גם בעיות מתמטיות קומבינטוריות העוסקות בהן, שהחשובה שבהן היא שאלת מספרם של אבני הפוליאומינו מגודל נתון - שאלה שטרם נמצאה לה תשובה משביעת רצון.
היסטוריה[עריכת קוד מקור | עריכה]
בעיית הספירה העתיקה ביותר הידועה שניתן לשייך לפוליאומינו היא זו של ספירת התבניות השונות שניתן ליצור על לוח משחק הגו באמצעות חמש אבנים שיוצרות צורה "קשירה" - היה ידוע כבר מימי קדם כי מספר זה הוא 12. עם זאת, עיסוק מתמטי של ממש בפוליאומינו לא החל עד למאה ה-20. חידות העוסקות בפוליאומינו התפרסמו כבר בשנת 1907, ומספר מאמרים בנושא חידות פוליאומינו התפרסמו בשנות ה-30 וה-40 בכתב עת שעסק בעיקר בחידות שחמט.
השם "פוליאומינו" נטבע בידי סולומון גולומב בשנת 1953 בהרצאה שנשא במועדון המתמטיקה של אוניברסיטת הרווארד. גולומב תרם רבות לפרסום הפוליאומינו בקרב הקהילה המתמטית, בפרט בספרו "Polyominoes" משנת 1965 שסקר את המחקר שהתבצע בתחום עד אז. בנוסף אליו, פרסם מרטין גרדנר חידות פוליאומינו רבות בטורו בירחון "סיינטיפיק אמריקן" ותרם לפופולריזציה שלהם. מרבית החידות סבבו סביב בעיות ריצוף שונות - האם ניתן, בהינתן קבוצה מסוימת של פוליאומינו, לרצף באמצעותם שטח מסוים. החידה המפורסמת ביותר בהקשר זה היא האם ניתן לרצף לוח שחמט 8x8 שממנו הורידו את שתי הפינות הנגדיות, בעזרת חתיכות של דומינו בלבד.
בהדרגה, ועם התפתחות המחשב עבר עיקר המחקר בפוליאומינו לשאלה הקומיבנטורית של מנייתם. החל משנות ה-70 החלו להתפרסם אלגוריתמים לא טריוויאליים למטרה זו והיא יצרה עניין גם בקרב פיזיקאים.
הפרסום הגדול ביותר לו הפוליאומינו זכו (אם כי לא תחת שם זה) הוא במשחק המחשב טטריס משנת 1985 שבו "מככבים" פוליאומינו בעלי ארבעה ריבועים. המשחק עצמו הוא דוגמה לפאזל סטנדרטי של ריצוף באמצעות פוליאומינו, כשנוסף אליו מימד של זריזות מחשבה ואי ודאות (לא ידוע מה עומדת להיות סדרת האבנים שבאמצעותה יש לרצף).
ריצופים באמצעות אבני פוליאומינו[עריכת קוד מקור | עריכה]
החידות ה"קלאסיות" הנוגעות לפוליאומינו הן חידות של ריצוף שטחים סופיים באמצעות קבוצה נתונה של פוליאומינו. כך למשל נמכרים משחקים המורכבים מלוח ומספר אבני פוליאומינו שמסוגלות לרצף אותו, ועל השחקן לגלות את הריצוף.
לעיתים השאלה המעניינת יותר היא מתי לא קיים ריצוף שכזה. טכניקה סטנדרטית לפתרון בעיות כאלו מבוססת על צביעת האזור שאותו מעוניינים לרצף בצבעים שונים, ואז המחשה של תכונה הנוגעת לצבעים הגלויים שנשמרת גם כאשר מניחים אבני פוליאומינו על חלק מהאזור.
מבחינה חישובית, בעיות הריצוף הללו כולן כריעות, שכן קיים רק מספר סופי של דרכים שבהן ניתן לנסות ולרצף שטח באמצעות אבני פוליאומינו, אך מעבר על כל האפשרויות עשוי לדרוש זמן רב; אכן, הבעיה הכללית, של הכרעה האם שטח סופי ניתן לריצוף באמצעות קבוצת אבני פוליאומינו נתונה היא NP-שלמה, כלומר נמנית עם אוסף של בעיות שהקושי החישובי שלהן אינו מוכח, אך סביר מאוד להניח שהן אכן קשות.
הבעיה הופכת לקשה פי כמה כאשר עוברים לדבר על ריצופים אינסופיים - דהיינו, יש לרצף את כל המישור באמצעות אינסוף עותקים מתוך קבוצת אבני פוליאומינו נתונה. בשנת 1966 הוכיח גולומב כי לא קיים אלגוריתם הפותר את הבעיה הכללית (כלומר, שמסוגל להתמודד עם קבוצת אבני פוליאומינו מכל גודל שהוא), לאחר שהראה כי קיום אלגוריתם שכזה היה מאפשר לפתור את בעיית אריחי ואנג, שהוכחה קודם לכן כבלתי כריעה. עם זאת, בשנת 1984 התגלה כי עבור פוליאומינו בודד (כאשר לא מתירים סיבובים או שיקופים שלו), בעיית הריצוף כריעה ואף פתירה בזמן יעיל.
הכללות של פוליאומינו[עריכת קוד מקור | עריכה]
ישנם מספר הכללות של הרעיון של הפולינומינוים לצורות נוספות.
פוליאמונדים[עריכת קוד מקור | עריכה]
הפוליאמונדים (polyiamonds) הם צורות הבנויות מחיבור יחדיו של משולשים שווי צלעות:
-
המוניאמונד (moniamond)
-
הדיאמונד (diamond)
-
הטריאמונדים (triamond)
-
הטטרימונדים (tetriamonds)
-
הפנטיאמונדים
-
ההקסיאמונדים
פוליהקסים[עריכת קוד מקור | עריכה]
הפוליהקסים (polyhexes) הם צורות הבנויות מחיבור יחדיו של משושים משוכללים:
-
המונוהקס (monohex)
-
הדיהקס (Dihex)
-
הטריהקסים
-
הטטרהקסים
-
הפנטהקסים
-
ההקסהקסים
פולידלתונים[עריכת קוד מקור | עריכה]

הפולידלתונים (polykites) הם צורות הבנויות מחיבור יחדיו של דלתוני ריצוף. בכל הצורות הללו החידות הבסיסיות עוסקות בריצופים של המישור בעזרתן, וכן בריצופים של צורות ספציפיות בעזרתן.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- פוליאומינו, באתר MathWorld (באנגלית)
- פוליאומינו, באתר אנציקלופדיה בריטניקה (באנגלית)








