פונקציה חד-כיוונית
| בעיות פתוחות במדעי המחשב: האם קיימות פונקציות חד-כיווניות?
(בעיות פתוחות נוספות במדעי המחשב) |
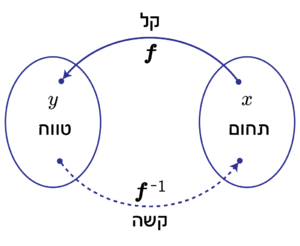
במדעי המחשב ובקריפטוגרפיה, פונקציה חד-כיוונית היא פונקציה שממירה קלט לפלט באופן שקשה מאוד מבחינה חישובית להפוך את הפונקציה, דהיינו לשחזר את הקלט בהינתן הפלט.
ביתר פירוט, בהינתן קלט כלשהו , קל לחשב את הפלט על ידי הפעלת הפונקציה החד-כיוונית בזמן פולינומי, דהיינו במהירות וביעילות אולם הפעולה ההפוכה שהיא בהינתן הפלט חישוב הוא משימה קשה חישובית. בניסוח פורמלי לא קיים אלגוריתם פולינומי הסתברותי המקבל את ומצליח למצוא כלשהו המקיים את אלא בהסתברות זניחה. הקושי החישובי בהיפוך הפונקציה מודד את כוח החישוב הדרוש כדי למצוא זוג של (קלט, פלט) מתאימים, אך אינו אומר דבר על מידע חלקי הזולג מהפונקציה. סיבית שהסיכוי לחשב אותה הוא זניח בהינתן נקראת סיבית קשה.
פונקציה חד-כיוונית היא מאבני הבניין של הקריפטוגרפיה המודרנית ומשמשת כפרימיטיב בפרוטוקולים קריפטוגרפיים רבים. שימוש נפוץ בפונקציה חד-כיוונית הוא כפונקציית גיבוב. אין הוכחה לקיומה של פונקציה חד-כיוונית מבחינה מתמטית - כי להוכחה כזו תהיינה השלכות מרחיקות לכת על תורת הסיבוכיות, אלא רק שקיימות מועמדות מעשיות לפונקציות חד-כיווניות שההשערה היא שקשה מאוד להפוך אותן. על בסיס השערה זו ניתן לבנות מערכת הצפנה שתהיה בטוחה כל עוד ההשערה נותרת בעינה. למעשה אפשר להוכיח שפונקציה חד-כיוונית היא תנאי הכרחי כמעט בכל משימה קריפטוגרפית. בהצפנה סימטרית וא-סימטרית כאחד. למשל צופן בלוקים מבוסס על תמורה פסאודו-אקראית שהיא פרימיטיב קריפטוגרפי המבוסס על ההשערה שפונקציה חד-כיוונית קיימת.
הפונקציות הקיימות כיום בשימוש מעשי נחשבות למועמדות טובות במובן שטרם נמצאה דרך קלה להפוך אותן. למשל AES נחשב לפונקציה חד-כיוונית אם כי לא הוכח תאורטית והוא אחד האלגוריתמים הנפוצים ביותר בהצפנה מודרנית. מהיבט תאורטי ניתן לבנות פונקציה חד-כיוונית מוכחת תחת מודל ביטחון אסימפטוטי או אחר אולם חסרונה הוא שיעילותה נמוכה בהשוואה לפונקציות הקיימות בשימוש מעשי. הבעיה העיקרית בקריפטוגרפיה מודרנית היא לגשר על הפער בין הוכחות תאורטיות לבין יישום מעשי יעיל.
הגדרה[עריכת קוד מקור | עריכה]
תהי פונקציה המקבלת קלט באורך כלשהו מבצעת חישוב מסוים ומחזירה פלט באורך כלשהו (המיוצג על ידי הכוכבית). הפונקציה תקרא חד-כיוונית אם מתקיימים התנאים הבאים:
- ניתנת לחישוב בזמן פולינומי.
- לכל מכונה הסתברותית פולינומית ופונקציה הנקראת פונקציית זניחות, עבור קלטים באורך כלומר , מתקיים:
| . |
הסבר[עריכת קוד מקור | עריכה]
התנאי הראשון קובע שהפונקציה קלה לחישוב. כלומר בעלת סיבוכיות פולינומית. התנאי השני מהווה את עיקר ההגדרה, הוא קובע שלכל יריב בעל עוצמת חישוב פולינומית לכל היותר, סיכויו זניח להצליח "להפוך" את הפונקציה. אם ליריב ידוע , הסיכוי שיימצא כלשהו כך ש- זניח. גם אם חושב במקור כתמונה של ערך , ייתכן שיהיו קלטים נוספים הממופים על ידי לאותו ערך. לכן היריב נדרש למצוא אחד מהם ולאו דווקא את הערך המקורי .
פונקציה שאינה חד-כיוונית אינה בהכרח קלה להפיכה בכל המקרים או ברוב המקרים. למעשה ההגדרה ההופכית להגדרת פונקציה חד-כיוונית היא שקיים אלגוריתם הסתברותי פולינומי ופונקציית זניחות כך שהאלגוריתם מצליח להפוך את הפונקציה בהסתברות שהיא לפחות כאשר הקלט נבחר באקראי. אם לדוגמה קיים אלגוריתם שמסוגל להפוך את הפונקציה בהסתברות מסוימת רק עבור קלטים זוגיים ולא עבור קלטים אי-זוגיים היא אינה נחשבת חד-כיוונית אפילו לא חלקית.
כל פונקציה ניתנת להפיכה, בהינתן מספיק זמן. למעשה אפשר להפוך את הפונקציה פשוט על ידי ניסוי כל האפשרויות או מחצית מהאפשרויות במקרה הממוצע, להתקפה כזו קוראים כוח גס. אולם סיבוכיות אלגוריתם כזה היא מעריכית. עובדה זו למעשה מוכיחה כי פונקציה חד-כיוונית נקראת כך רק ביחס לעוצמת המחשוב הדרושה כדי להפוך אותה.
תמורה חד-כיוונית[עריכת קוד מקור | עריכה]
לעיתים יש צורך בפונקציה חד-כיוונית עם תכונה מבנית נוספת. אם הפונקציה משמרת אורך כלומר עבור כל והפונקציה היא חד-חד-ערכית ועל היא נקראת פרמוטציה (תמורה). בניסוח פורמלי:
תהי פונקציה חד-כיוונית משמרת אורך, ונניח ש- מגבילה את התחום של כך ש- מזה נובע . היא תקרא פרמוטציה חד-כיוונית אם עבור כל הפונקציה היא חד-חד-ערכית ועל.
בניגוד לפונקציה חד-כיוונית בפרמוטציה חד-כיוונית עבור כל קיים רק מקור יחיד לכן . המשמעות היא ש- למעשה מכיל מידע לגבי ולמרות זאת עדיין קשה למצוא אותו.
משפחה של פונקציות חד-כיווניות[עריכת קוד מקור | עריכה]
ההגדרה של פונקציה או תמורה חד-כיוונית לא מטיבה לתאר את הפונקציות או התמורות החד-כיווניות המועמדות בפועל, כי היא מדברת על פונקציה יחידה מעל מקור ותמונה אין סופיים. הגדרה יותר קולעת היא שקיים אלגוריתם המפיק פרמטר כלשהו המגדיר פונקציה/תמורה כלשהי מעל מקור כלשהו , כך שהיא תהיה חד-כיוונית כמעט לגמרי למעט הסתברות זניחה מעל . מפני שכל ערך של מגדיר פונקציה אחרת אפשר להתייחס אליה כאל "משפחה" של פונקציות/תמורות חד-כיווניות. ההגדרה כעת בניסוח פורמלי היא, השלישייה המייצגת אלגוריתם פולינומי הסתברותי, נקראת משפחה של פונקציות אם:
- אלגוריתם ההכנה Gen מפיק פרמטר כך שמתקיים שמגדיר את המקור ותמונה של הפונקציה המוגדרת להלן.
- אלגוריתם הדגימה Samp פולט בהינתן אלמנט מתוך בהתפלגות אחידה למעט הסתברות זניחה ביחס ל-
- אלגוריתם ההערכה , בהינתן ו- פולט את האלמנט . מציינים זאת על ידי .
באופן דומה כדי לקבל הגדרה של משפחה של תמורות, ההבדלים הם שבתמורות והפונקציה היא חד-חד-ערכית ועל. היתר זהה. כעת הניסוי משתנה בהתאם:
- תחילה מריצים את Gen כדי להפיק את ואז את הפונקציה כדי לקבל את ואז מחשבים את .
- האלגוריתם מקבל את ואת ומפיק את .
- תוצאת הניסוי היא '1' אם .
פונקציה חד-כיוונית במובן החלש[עריכת קוד מקור | עריכה]
ניתן להגדיר פונקציה חד-כיוונית במובן חלש, שהא פונקציה הניתנת לחישוב בזמן פולינומי, והעונה לתנאי הבא:
- לכל מכונת-טיורינג מטילת מטבעות ולכל קבוע , עבור קלטים ארוכים מספיק , מתקיים, [1].
ניתן להראות שקיומה של פונקציה חד-כיוונית במובן החלש מעיד על קיומה של פונקציה חד-כיוונית במובן החזק, כלומר, בעזרת פונקציה חד-כיוונית במובן חלש, ניתן לבנות פונקציה חד-כיוונית במובן החזק[דרוש מקור].
פונקציה חד-כיוונית עם דלת צונחת[עריכת קוד מקור | עריכה]
פונקציה חד-כיוונית עם דלת צונחת (באנגלית: trapdoor one-way function), היא פונקציה חד-כיוונית שקל לחשבה בכיוון אחד אך קשה לחשבה בכיוון ההפוך אלא אם כן קיים מידע נוסף הנקרא "דלת צונחת" שמאפשר לחשב את הפונקציה ההופכית בקלות. בניסוח פורמלי, הפונקציה קלה לחשוב בעוד שהפונקציה קשה מאוד לביצוע ללא הרמז הנוסף. המידע הנוסף נקרא בהקשר זה מפתח פענוח.
דוגמה קלאסית לפונקציה עם דלת צונחת היא מציאת שורש ריבועי מודולו מספר פריק שהוא כפולה של שני ראשוניים גדולים. העלאה בריבוע של מספר גדול היא פעולה קלה במחשב, בעוד שהפעולה ההפוכה קשה, לא קיים אלגוריתם יעיל לחישוב שורש ריבועי מודולו מספר פריק. לעומת זאת קיימים אלגוריתמים לחישוב שורש ריבועי מודולו מספר ראשוני. אם ידועים הגורמים הראשוניים של המודולוס אפשר לחשב תחילה את השורשים הריבועים של המספר מודולו כל אחד מהגורמים ואז לחלץ מזה ארבעה פתרונות אפשריים מודולו המספר הפריק. במקרה זה, ידיעת הגורמים הראשוניים של המודולוס מאפשרת לבצע את הפעולה ההפוכה, קרי הוצאת שורש בקלות. לכן הגורמים הראשוניים של המודולוס נחשבים מהיבט זה דלת צונחת. רק מי שיודע מה הם הגורמים הראשוניים יכול לפתור את הבעיה בקלות.
המונח דלת צונחת הוטבע לראשונה על ידי ויטפילד דיפי ומרטין הלמן במאמרם משנת 1976 "כיוונים חדשים בהצפנה"[2]. מאז הוצעו מועמדים רבים לפונקציה חד-כיוונית עם דלת צונחת. קיים מגוון בעיות מתמטיות קשות לא בהכרח מתורת המספרים שאפשר לבסס עליהן פונקציה חד-כיוונית. לדוגמה בעיית מציאת הווקטור הקצר ביותר בתורת הסריגים. אולם המכשול העיקרי הוא שכאשר מוסיפים דלת צונחת, הבעיה הופכת בעצם למקרה פרטי של הבעיה הכללית ואין הוכחה שהיא נותרת קשה לפתרון כמו הבעיה הכללית ולא הוחדרו חולשות כלשהן מבלי משים. מקרה אחד מעניין הוא הצפנת תרמיל. לאחר מחקר של שנים הסתבר שכל הניסיונות לייצר פונקציה חד-כיוונית עם דלת צונחת המבוססת על בעיית התרמיל, כשלו. למרות חשיבותה הרבה בקריפטוגרפיה קשה מאוד למצוא פונקציה חד-כיוונית עם דלת צונחת שהיא גם יעילה וגם בטוחה.
קיימות כמה משפחות של מועמדים לפונקציות חד-כיווניות עם דלת צונחת שההשערה לגביהן שהן בטוחות:
- פונקציות מבוססות פירוק לגורמים כמו RSA ורבין.
- פונקציות מבוססות בעיית הלוגריתם הדיסקרטי.
- פונקציות מבוססות בעיות מתורת הסריגים.
מועמדים לפונקציה חד-כיוונית[עריכת קוד מקור | עריכה]
קיומן של פונקציות חד-כיווניות מחייב שקיימות בעיות חישוביות אשר שייכות ל-NP ואינן שייכות ל-BPP (מחלקת הבעיות אשר ניתנות לפתרון בזמן ריצה פולינומי עם אלגוריתמים אקראיים), מאחר שלא ידוע האם (שאלה חזקה יותר, ומפורסמת יותר, היא האם P=NP), לא ניתן להצביע על קיומן של פונקציות כאלה. יתר על כן, ייתכן ש-, ובכל זאת לא יהיו קיימות פונקציות חד כיווניות. (כיוון שנדרש מהן שהיפוכן קשה במקרה הממוצע ולא רק במקרה הקשה). דרך פרקטית להגדיר פונקציה חד-כיוונית היא פונקציה חד-כיוונית חישובית המבוססת על ההשערה שלא קיים אלגוריתם פולינומי המסוגל להפוך אותה ביעילות.
הדוגמה הטובה ביותר היא בעיית פירוק לגורמים ראשוניים של מספר שלם, שהיא מקור טוב לפונקציה חד-כיוונית בהנחה שפירוק לגורמים היא בעיה מעשית קשה. מצד אחד בהינתן שני מספרים שלמים פונקציית הכפל שלהם קלה, מצד שני בהינתן מספר אי-זוגי שהוא כפולה של שני מספרים ראשוניים גדולים, מציאת הגורמים הראשוניים שלו היא בעיה קשה. יש לשים לב שלא תמיד הבעיה קשה, אם זוגי או שגורמיו קטנים קל להפוך את הפונקציה. הצפנת RSA מבוססת על הנחה זו.
דוגמה אחרת היא בעיית תרמיל הגב שאינה קשורה ישירות לתורת המספרים שידועה כבעיה NP-קשה עליה מבוססת הצפנת תרמיל. נתונה סדרה של שלמים לא בהכרח בסדר עולה ונתון שלם כלשהו, בעיית התרמיל היא למצוא תת-סדרה של שסכומה הוא . החד כיווניות נובעת מהעובדה שבעוד שבחירת תת-סדרה וחישוב סכומה היא משימה קלה, הרי שבכיוון ההפוך בהינתן ערך כלשהו, מציאת תת-הסדרה שסכומה שווה לערך זה בדיוק, היא משימה קשה. אין זו הוכחה ש- וזה לא מעיד בהכרח שפונקציה חד-כיוונית קיימת, אלא שבעיית התרמיל לא ניתנת לפתרון במקרה הגרוע בזמן פולינומי, בעוד שפונקציה חד-כיוונית נדרשת שתהיה בלתי הפיכה "כמעט תמיד". הטענה שפונקציית תרמיל-הגב האמורה חד-כיוונית מסתמכת רק על כך שלא ידוע על אלגוריתם טוב הפותר את הבעיה בזמן פולינומי ולא על ההנחה שהבעיה הכללית היא NP-קשה.
כיום ידוע שלבעיית התרמיל קשר הדוק לתורת הסריגים. למעשה כל אלגוריתם שפותר את בעיית הווקטור הקצר ביותר יכול לשמש לפתרון בעיית התרמיל. למשל אלגוריתם LLL נחשב לאלגוריתם הטוב ביותר לפתרון בעיות בתורת הסריגים. אלגוריתם זה למעשה היה בסיס להתקפה קריפטוגרפית על כמה מערכות ההצפנה שהתבססו על בעיית התרמיל.
שימושים[עריכת קוד מקור | עריכה]
הצפנת מפתח ציבורי[עריכת קוד מקור | עריכה]
הצפנה בשיטת מפתח ציבורי שמכונה גם הצפנה א-סימטרית, היא בעצם פונקציה חד-כיוונית עם דלת צונחת. לפונקציות אלה התכונה שישנו מידע אשר ידוע רק לנמען המורשה של ההודעה (המפתח הפרטי) שבעזרתו קל לחשב את הפונקציה ההופכית, כלומר לבצע את פענוח ההודעה המוצפנת. מי שאין בידו המידע הזה ומנסה לפענח את ההודעה המוצפנת, עומדת לפניו משימה חישובית קשה מאוד. אלגוריתם RSA הנזכר לעיל עושה שימוש בפונקציה מסוג זה.
העברת סיסמה מוצפנת[עריכת קוד מקור | עריכה]
מקובל להשתמש בפונקציית גיבוב חד-כיוונית כדי להעביר סיסמה למחשב המאמת (השרת). דוגמה: השרת המאמת שולח משפט למחשב ברשת, זה האחרון לוקח את המשפט, מוסיף אליו את הסיסמה לאימות ומעביר אותם לפונקציית גיבוב חד-כיוונית. את הפלט (המהווה הסיסמה המוצפנת) הוא שולח לשרת. השרת מבצע את אותה הפעולה בדיוק. אם שני הפלטים זהים - יאשר השרת כי הסיסמה נכונה.
ראו גם[עריכת קוד מקור | עריכה]
- סיבית קשה של פונקציה חד-כיוונית
- פונקציית גיבוב קריפטוגרפית
- קריפטוגרפיה
- הנדסה לאחור
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Oded Goldreich (2001). Foundations of Cryptography: Volume 1, Basic Tools. Cambridge University Press. פרקים מהספר באתר המחבר
- Jonathan Katz and Yehuda Lindell (2007). Introduction to Modern Cryptography.
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ ההסתברות היא על כלל הקלטים ועל הטלות המטבע של המכונה A.
- ^ New Directions in Cryptography












![{\displaystyle \Pr _{x\in \{0,1\}^{n}}[{\mathcal {A}}(f(x))\in f^{-1}(f(x))]\leq {\text{negl}}(n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0a4f367b05db047d97c234a79d1834c924cb97d)























![{\displaystyle \Pr[A(f(x))=f^{-1}(f(x))]<1-{\frac {1}{n^{c}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a2d8d5ca7d437c410f1ec15425e8c81e310b82d)






