אלגוריתם דויטש-ג'וזה
אלגוריתם דויטש-ג'וזה הוא אלגוריתם קוונטי להבדלה בין פונקציה קבועה לבין פונקציה מאוזנת. האלגוריתם מהווה דוגמה ליתרון המתקבל משימוש של מחשב קוונטי על פני מחשב קלאסי. האלגוריתם פורסם על ידי ריצ'רד ג'וזה ודייוויד דויטש בשנת 1992, והניח את היסודות לפיתוח אלגוריתם גרובר ואלגוריתם הפיקטור של פיטר שור.
הגדרה[עריכת קוד מקור | עריכה]
תהי פונקציה המקבלת קלט באורך ביטים, ופולטת פלט באורך ביט יחיד, כך שמתקיים אחד מהשניים:
- היא פונקציה קבועה, כלומר, לכל מתקיים , או שלכל מתקיים ; או
- היא פונקציה מאוזנת, כלומר למחצית מה--ים מתקיים ולשאר
אלגוריתם דויטש-ג'וזה מקבל כקלט את הפונקציה [1], ומחזיר כפלט האם היא קבועה או מאוזנת. האלגוריתם עושה זאת על ידי הפעלה של הפונקציה פעם יחידה בלבד.
פתרון קלאסי[עריכת קוד מקור | עריכה]
באופן קלאסי, זיהוי האם פונקציה קבועה או מאוזנת מצריך לכל הפחות הפעלות של פונקציית הקלט עם ערכי שונים. אם בכלל הפעלות הפונקציה מתקבל אותו ערך אזי היא קבועה, ואם בשתיים מההפעלות מתקבלים ערכים שונים, אזי הפונקציה היא מאוזנת. לא קיים פתרון דטרמיניסטי המפעיל את הפונקציה פחות מ פעמים, שכן תמיד ייתכן מצב בו הערכים שעליהם נשאלה הפונקציה מקיימים ועדיין שאר הערכים מקיימים , כלומר הפונקציה מאוזנת.
מצד שני, קיימים פתרונות הסתברותיים לבעיה זו. לדוגמה, ניתן להגריל כמות של קלטים שונים ולבדוק את ערך הפונקציה עבור קלטים אלו בלבד. במידה ומתקיים קיימת הסתברות שהאלגוריתם יטעה, אך הסתברות זו נחשבת זניחה מכיוון שהיא קטנה מ-.
תיאור האלגוריתם[עריכת קוד מקור | עריכה]
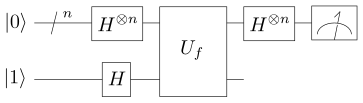
האלגוריתם הקוונטי מתואר בתרשים משמאל. המעגל מקבל כקלט אוגר קוונטי המכיל קיוביטים. ניתן להסתכל על הקלט כשני אוגרים המאותחלים ל . על כל אחת מהכניסות מופעל שער הדמר, ומצבם המשותף ניתן כעת לביטוי בתור . כעת מופעלת הפונקציה הקוונטית על האוגר, כאשר הכניסות הראשונות הן הקלט, ואילו הכניסה האחרונה משמשת עבור הפלט. לאחר הפעלת הפונקציה מצב האוגר הוא .
העיקרון עליו מבוסס האלגוריתם הוא הבא: אם קיוביט הפלט ניתן לרישום בתור ואילו עבור אותם -ים עבורם נקבל כלומר הסימן של האוגר משתנה בהתאם לערך הפונקציה , והאוגר ניתן לרישום בתור . נשים לב שהקיוביט האחרון אינו תלוי בערך של הפונקציה, ערכו תמיד וניתן להתעלם ממנו בהמשך.
כעת נפעיל בשנית שער הדמר על האוגר ונבדוק את שני המצבים האפשריים:
- אם הפונקציה הייתה קבועה לערך 0, אזי האוגר היה מהצורה . לאחר הפעלת השער יהיה ערכו ועל כן מדידתו בבסיס החישוב תתן את התוצאה בהסתברות 1.
- אם הפונקציה הייתה מאוזנת, אז חצי מהערכים הם בעלי פאזה חיובית ומחציתם בעלי פאזה שלילית. נשים לב שלאחר הפעלת שער הדמר על אוגר בעל ערך כלשהו, התוצאה היא סכום משוקלל של כלל הערכים האפשריים כאשר הפאזה של כל אבר נקבעת בהתאם לערך . כמו כן, נשים לב שהפאזה של האבר בסכום זה היא תמיד חיובית, ללא תלות בערכו של . לפיכך, כאשר נפעיל את השער הדמר על סופרפוזיציה של אברי הבסיס האפשריים כאשר הפאזה של חציים חיובית ושל חציים שלילית - במוצא השער האבר יתאפס, ומדידה בבסיס החישוב לעולם לא תפיק את התוצאה .
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ ליתר דיוק, האלגוריתם מקבל קופסה שחורה המממשת את הפונקציה

























