דיאגרמת פיינמן
דיאגרמת פיינמן היא ייצוג תרשימי של תהליכים המתרחשים בין חלקיקים בתורת השדות הקוונטית, על ידי מיפוי מסלוליהם והתופעות הקוונטיות הנלוות להם בתוך מרחב נתון ('שדה'). היא הומצאה על ידי הפיזיקאי האמריקאי-יהודי ריצ'רד פיינמן והוצגה לראשונה בשנת 1949. הדיאגרמה נתנה הסבר ויזואלי פשוט יותר להבנה של תופעה מורכבת יחסית בפיזיקת חלקיקים.
פיתוח הדיאגרמה[עריכת קוד מקור | עריכה]

ריצ'רד פיינמן קיבל את ההשראה לדיאגרמות אלה בעקבות הפלקסגון שאותו הציג לו ארתור סטון (אנ') בשנת 1939. הוא בנה דיאגרמה המראה כיצד ניתן לעבור בין צדדיו השונים של פלקסגון בעל שישה צדדים המכונה הקספלקסגון[1]. מקרה זה הוא דוגמה לדרך בה שעשועי מתמטיקה יכולים להוביל להתפתחויות בתחום המדע.
צורת הגרף[עריכת קוד מקור | עריכה]
הדיאגרמה מציגה את תנועת החלקיק, כאשר ציר אחד מסמן את הזמן והשני את המרחב. חלקיקים מיוצגים על ידי קווים, אשר עשויים להיות מפותלים או ישרים, עם חץ או בלי חץ, בהתאם לסוג החלקיק. נקודה בה הקווים מתחברים אחד לשני נקראת "צומת אינטראקציה", או פשוט "צומת". ישנם שלושה סוגים שונים של קווים: "קווים פנימיים" מחברים שני צמתים, "קווים נכנסים" נמתחים מ"העבר" אל תוך צומת ומייצגים את המצב הראשוני, ו"קווים יוצאים" נמתחים מצומת אל "העתיד" ומייצגים את המצב הסופי.

| משמעות | סימון בגרף |
|---|---|
| פרמיון | |
| אנטיפרמיון | |
| בוזוני W±, Z | |
| גלואון (g) | |
| בוזון היגס | |
| Terminator
(בוזון היגס שעובר תהליך של עיבוי בוז-איינשטיין) |
| בוזונים | לפטונים | ||
|---|---|---|---|
| משמעות | סימון בגרף | משמעות | סימון בגרף |
| פוטון | 
|
אלקטרון | |
| בוזון Z | 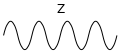
|
פוזיטרון | |
| בוזון W + | 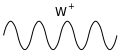
|
מיואון | |
| בוזון W - | 
|
נייטרינו | |
חוקי פיינמן[עריכת קוד מקור | עריכה]
ישנם מספר חוקים על מנת ליצור דיאגרמה המייצגת תהליך פיזיקלי:
- כל נקודת מפגש צריכה להיות מיוצגת על ידי נקודה.
- כל בוזון צריך להיות מיוצג על ידי קו גלי.
- פרמיון צריך להיות מיוצג על ידי קו ישר המחבר שתי נקודות.
- כל קו גלי חייב להיות מחובר בקצהו לנקודת מפגש של שני קווים מלאים. כלומר, אין אפשרות למגע בין קו גלי לקו ישר שלא בנקודת מפגש של שני קווים ישרים.
ייצוג פשוט של תהליכים פיזיקליים[עריכת קוד מקור | עריכה]

הדיאגרמה מאפשרת לראות תהליכים פיזיקליים בצורה ויזואלית, כשבלעדיה היו נדרשות נוסחאות רבות ומסובכות לתפישה מהירה שלהם. בנוסף, בדיאגרמה מתוארות האינטראקציות בצורה גרפית פשוטה כקווים וצמתים, כאשר גם בוזונים, המייצגים שדות, מיוצגים כחלקיקים לפשטות השרטוט.
תנועה נגד ציר הזמן[עריכת קוד מקור | עריכה]
בדיאגרמת פיינמן, האנטי-חלקיקים (לדוגמה הפוזיטרון) נעים בניגוד לציר הזמן וכביכול נעים אחורה בזמן. פיינמן פירש זאת ממשוואת דיראק לפיה לאנטי-חלקיקים יש מסה וספין זהים לזה של החלקיק הרגיל, אך המטען החשמלי שלהם הפוך. משוואה זו הובילה לתוצאה לפיה לאנטי-חלקיקים יש אנרגיה שלילית[2]. פיינמן השתמש בפרשנותו של המתמטיקאי והפיזיקאי ארנסט שטוקלברג (אנ') של הפוזיטרון כאלקטרון הנע אחורה בזמן.
בתרבות הפופולרית[עריכת קוד מקור | עריכה]
- בסיטקום הטלוויזיוני המפץ הגדול נעשה שימוש בדיאגרמה שלעיל המייצגת חלקיק וירטואלי ההופך לזוג קווארק - אנטי-קווארק, בפרק "The Bat Jar Conjecture".
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- "Space-Time Appxoach to Quantum Electxotiynamics" – מאמרו של ריצ'רד פיינמן משנת 1949, שבו הציג את רעיון הדיאגרמות לראשונה.
- Draw Feynman Diagram Online – אתר בו ניתן ליצור דיאגמות פיינמן בפשטות.
- דיאגרמת פיינמן, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Hilton, P.; Pedersen, J. & Walser, H. (1997). "The faces of the tri-hexaflexagon". Mathematics Magazine. 70 (4): 243–251. doi:10.1080/0025570X.1997.11996549..
- ^ Feynman, R. P. (1949). "The theory of positrons". Physical Review. 76 (6): 749–759. Bibcode:1949PhRv...76..749F. doi:10.1103/PhysRev.76.749..
