מיון מיזוג
מיון מיזוג (באנגלית: Merge Sort) הוא אלגוריתם מיון רקורסיבי המתבסס על מיזוגם של מערכים ממוינים.
סיבוכיות זמן ריצה של מיון מיזוג היא , וסיבוכיות הזיכרון היא . סיבוכיות זמן ריצה של מיון מיזוג נחשבת ליעילה ביותר בקרב אלגוריתמים מבוססי השוואות.
תיאור האלגוריתם[עריכת קוד מקור | עריכה]

האלגוריתם הומצא על ידי ג'ון פון נוימן בשנת 1945. אלגוריתם זה מתבסס על אלגוריתם הפרד ומשול: שמחלק את הבעיה לשתי תת-בעיות קטנות יותר. את מיון המערך הוא מחלק למיון חציו הראשון של המערך ומיון חציו השני, פותר כל אחד מהם באמצעות קריאה רקורסיבית (הפרד). בתום פתרון תתי-הבעיות, ממזג האלגוריתם את שני חצאי המערך, הממוינים כעת, למערך ממוין גדול המכיל את כל איבריהם (משול) וזהו בדיוק פתרון הבעיה הראשונית.
מימוש מילולי[עריכת קוד מקור | עריכה]
ברמה העקרונית, עובד מיון-מיזוג בצורה הבאה:
מיין-מזג n איברים
- אם n=1 (המערך של איבר אחד ממילא ממוין (באופן ריק)) חזור
- מיין-מזג את n/2 האיברים הראשונים
- מיין-מזג את n/2 האיברים האחרונים
- מזג את 2 תוצאות המיון
בפסאודו קוד, המזכיר את שפת C, יראה האלגוריתם כך:
mergesort(Array m)
{
if length(m) ≤ 1
return m
else
{
middle = length(m) / 2
for each x in m up to middle
add x to left
for each x in m after middle
add x to right
left = mergesort(left)
right = mergesort(right)
result = merge(left, right)
return result
}
}
מימוש המיזוג[עריכת קוד מקור | עריכה]
מיזוג שני מערכים ממוינים הוא מטלה פשוטה. נסתכל על האיבר הראשון בכל מערך (המערכים ממוינים ולכן זהו האיבר הקטן ביותר בכל מערך), האיבר הקטן מביניהם הוא האיבר הקטן ביותר שקיים (הוא קטן מכל איברי המערך שלו וקטן מהאיבר הראשון השני שקטן מכל איברי המערך שלו ולכן סה"כ הוא קטן מכל איברי המערכים) ולכן הוא יהיה האיבר הראשון במערך החדש. טיפלנו באיבר זה ולכן נסתכל על האיבר הבא באותו מערך, נמשיך להסתכל על האיבר הראשון במערך השני משום שבו עוד לא טיפלנו. כעת שוב אנו מסתכלים על שני האיברים הקטנים ביותר שקיימים ולכן הקטן מביניהם יהיה האיבר השני במערך החדש. נמשיך כך עד שנסיים את כל איבריו של מערך מסוים ואז נכניס ברצף את כל איברי המערך השני (הם כבר ממוינים כי המערך ממוין).
בשפה מקצועית יותר נאמר שאנו מצביעים על האיבר הראשון בכל מערך ואז מכניסים למערך החדש את האיבר הקטן יותר. אנו מקדמים את המצביע שהצביע על האיבר המוכנס באחד וחוזרים על התהליך. כאשר הגיע אחד המצביעים לסוף המערך, נכניס את יתר איברי המערך השני למערך החדש. מכיוון שעברנו על כל אחד מאיברי המערכים בדיוק פעם אחת וסה"כ קיימים איברים, סיבוכיות המיזוג .
בפסאודו קוד יראה המיזוג כך:
merge(left,right)
{
while length(left) > 0 and length(right) > 0
{
if first(left) ≤ first(right)
{
append first(left) to result
left = rest(left)
}
else
{
append first(right) to result
right = rest(right)
}
}
if length(left) > 0
append left to result
if length(right) > 0
append right to result
return result
}
להמחשה, נמזג את קבוצות המספרים הממוינות: 1,2,4,8,9,10,11 ו-3,7.
- האיברים הראשונים הם 1 ו-3. 1 קטן מ-3 ולכן נכניס את 1.
- כעת האיברים הראשונים הם 2 (1 הוכנס) ו-3 (לא טיפלנו בו עדיין). 2 קטן מ-3 ולכן נכניס את 2.
- כעת האיברים הראשונים הם 4 ו-3. 3 קטן מ-4 ולכן נכניס את 3.
- כעת האיברים הראשונים הם 4 ו-7. 4 קטן מ-7 ולכן נכניס את 4.
- כעת האיברים הראשונים הם 8 ו-7. 7 קטן מ-8 ולכן נכניס את 7.
- שים לב שלא נותרו עוד מספרים בקבוצת המספרים השנייה, נכניס את יתר קבוצת המספרים הראשונה: 8,9,10,11.
נראה כעת מהו המערך שהתקבל: 1,2,3,4,7,8,9,10,11. אלו הם בדיוק כל המספרים כאשר הם ממוינים כפי שציפינו.
דוגמה למימוש בשפת C++[עריכת קוד מקור | עריכה]
#include <iostream>
#include <time.h>
using namespace std;
const int ARR_LENGTH = 1000;
void merge (int arr [], int temp [], int left, int mid, int right)
{
int leftPlace = left, rightPlace = mid +1;
bool leftOver = false, //all the left data was merged
rightOver = false; //all the right data was merged
for (int place = left; place <= right; place++)
{
if (leftPlace > mid) leftOver = true;
if (rightPlace > right) rightOver = true;
temp [place] = (rightOver || !leftOver && arr [leftPlace] <= arr [rightPlace])? //the merge
arr [leftPlace ++] : arr [rightPlace ++];
}
for (int i = left; i <= right; i++) //return the merged data into the array
arr [i] = temp [i];
}
void mergeSort (int arr [], int temp [], int left, int right)
{
int mid = (right + left) /2;
if (mid > left) //more than one cell
mergeSort (arr, temp, left, mid);
if (right > mid +1) //more than one cell
mergeSort (arr, temp, mid +1, right);
merge (arr, temp, left, mid, right);
}
void sort (int arr [])
{
int temp [ARR_LENGTH]; //array aid
mergeSort (arr, temp, 0, ARR_LENGTH -1);
}
int main()
{
srand ( (unsigned int) (time(NULL))); //init the rand
int arr [ARR_LENGTH];
for (int i =0; i < ARR_LENGTH; i++)
arr [i] = rand () % 100; //insert data
for (int i =0; i < ARR_LENGTH; i++)
cout << arr [i] << " "; //print before sorting
cout << endl << endl;
sort (arr);
for (int i =0; i < ARR_LENGTH; i++)
cout << arr [i] << " "; //print after sorting
cout << endl;
return (EXIT_SUCCESS);
}
דוגמה למימוש בשפת C[עריכת קוד מקור | עריכה]
#include<stdio.h>
#define MAX 100
void mergeSort(int arr[], int low, int mid, int high);
void partition(int arr[], int low, int high);
int main()
{
int merge[MAX] = { 0 };
int i = 0;
int n = 0;
printf("Enter the number of elements in the array to sort (maximum %d elements): ", MAX);
scanf("%u", &n);
printf("Enter the value of the elements sort (type ENTER after each value): ");
for (i = 0; i < n; i++)
{
scanf("%d", &merge[i]);
}
partition(merge, 0, n - 1);
printf("After merge sorting elements are: ");
for (i = 0; i < n; i++)
{
printf("%d ", merge[i]);
}
return 0;
}
void partition(int arr[], int low, int high)
{
int mid = 0;
if (low < high)
{
mid = (low + high) / 2;
partition(arr, low, mid);
partition(arr, mid + 1, high);
mergeSort(arr, low, mid, high);
}
}
void mergeSort(int arr[], int low, int mid, int high)
{
int i = 0;
int m = 0;
int k = 0;
int l = 0;
int temp[MAX];
l = low;
i = low;
m = mid + 1;
while ((l <= mid) && (m <= high))
{
if (arr[l] <= arr[m])
{
temp[i] = arr[l];
l++;
}
else
{
temp[i] = arr[m];
m++;
}
i++;
}
if (l > mid)
{
for (k = m; k <= high; k++)
{
temp[i] = arr[k];
i++;
}
}
else
{
for (k = l; k <= mid; k++)
{
temp[i] = arr[k];
i++;
}
}
for (k = low; k <= high; k++)
{
arr[k] = temp[k];
}
}
דוגמה למימוש בשפת python 3[עריכת קוד מקור | עריכה]
def mergeSort(alist):
print("Splitting ",alist)
if len(alist)>1:
mid = len(alist)//2
lefthalf = alist[:mid]
righthalf = alist[mid:]
mergeSort(lefthalf)
mergeSort(righthalf)
i=0
j=0
k=0
while i < len(lefthalf) and j < len(righthalf):
if lefthalf[i] <= righthalf[j]:
alist[k]=lefthalf[i]
i=i+1
else:
alist[k]=righthalf[j]
j=j+1
k=k+1
while i < len(lefthalf):
alist[k]=lefthalf[i]
i=i+1
k=k+1
while j < len(righthalf):
alist[k]=righthalf[j]
j=j+1
k=k+1
print("Merging ",alist)
alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)
print(alist)
דוגמת הרצה[עריכת קוד מקור | עריכה]
השרטוט הבא מדגים כיצד ממיין האלגוריתם מערך בגודל 7 המכיל את הערכים: 38,27,43,3,9,82,10.
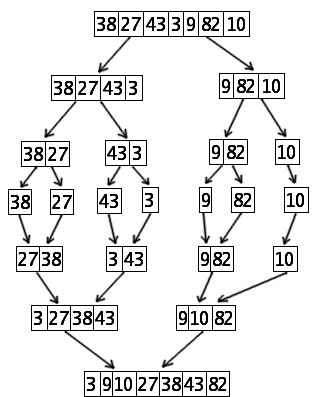
ניתוח סיבוכיות מיון-מיזוג[עריכת קוד מקור | עריכה]
פעולת ה"מיון" קוראת לפונקציה מחדש. הפעולה היחידה המתרחשת בפועל היא פעולת המיזוג. קל לחשב את סיבוכיות זמן הריצה של פעולה זו, בכל סיבוב של המיזוג מוכנס איבר אחד למערך, ומשום שקיימים איברים, מתבצעות פעולות. כעת נותר לחשב כמה פעמים פעולה זו מתבצעת, ובכל פעם לבדוק כמה איברים משתתפים בפעולה.
ננסה לחשב תחילה את מספר הפעמים שמתבצעת פעולת המיזוג. הפעולה מתבצעת בכל קריאה לפונקציה "מיון-מיזוג". הקריאה הראשונה תמזג בין שני חצאי מערכים בגודל (סה"כ איברים, סיבוכיות זמן ריצה . לפני-כן הקריאה הראשונה קוראת פעמיים למיון-מיזוג, פעם אחת עבור חצי המערך הראשון ופעם שנייה עבור חצי המערך השני. בכל קריאה יתבצע מיזוג של שני חצאי מערכים בגודל , סה"כ מדובר ב-4 מערכים ולכן יש סה"כ איברים שיתמזגו ושוב סיבוכיות זמן הריצה הכוללת היא . האלגוריתם ימשיך עד אשר כל המערכים יהיו בגודל 1 ואז נמזג אותם זוג-זוג, עדיין מדובר ב- איברים ולכן סיבוכיות זמן הריצה של כל פעולות המיזוג יחד היא .
נסתכל בכל פעם רק על חלק אחד של המערך המפוצל, נתחיל במערך הגדול ונשאר עם מערך בגודל ואז נמשיך להתבונן במערך בגודל וכן הלאה, עד אשר נגיע למערך בגודל 1. בכל שלב מתבצע מיזוג שזמן ריצתו , נותר רק לספור כמה שלבים כאלו יש.
בכל פעם נשלח למיון-מיזוג מערך שגודלו חצי מהמערך הקודם. לאחר קריאה אחת יהיה גודל המערך , לאחר שתי קריאות יהיה גודלו וכן הלאה. התהליך ייגמר כאשר גודל המערך הוא 1. אם התהליך כולו יימשך פעמים, יהיה גודל המערך . כדי שגודל זה יהיה 1 נדרוש . נוציא משני אגפי המשוואה ונקבל כי .
קבלנו שמתרחשות פעולות מיזוג שסיבוכיות זמן הריצה של כל אחת מהן היא .
סה"כ סיבוכיות זמן הריצה של האלגוריתם היא, אם כן, .
קיימת גם גרסה מקבילית של האלגוריתם המשתמשת ב מעבדים ופועלת בסיבוכיות של .
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- אוסף מצגות והדגמות אנימציה בנושא MergeSort
- מיון מיזוג בQueue
- מיון מיזוג, באתר MathWorld (באנגלית)
| אלגוריתמי מיון | ||
|---|---|---|
| רקע תאורטי | תורת הסיבוכיות • סימון אסימפטוטי • סדר מלא • רשימה • אלגוריתם תוך-מקומי • מיון יציב | |
| אלגוריתמי מיון | אקראי • בועות • בחירה • בסיס • הכנסה • מהיר • מיזוג • מנייה • מסרק • סלים • ערימה • רשת מיון • שייקר • של | |
| שונות | מיון טופולוגי • בעיית סידור הפנקייקים של גודמן | |
















