ערימת פיבונאצ'י
במדעי המחשב, ערימת פיבונאצ'י היא סוג של מבנה הנתונים ערימה שהומצא על ידי מייקל פרדמן ורוברט טרג'אן[1].
מבוא[עריכת קוד מקור | עריכה]
ערימה היא מבנה נתונים המשמשת למספר דברים, למשל, תור עדיפויות. היא מאפשרת לבצע במהירות הכנסה, מציאת מינימום, מחיקה והקטנת הערך. ערימה בינומית, הממומשת כאוסף עצים בינומיים, מאפשרת גם למזג במהירות שתי ערימות.
עם זאת, לעיתים נדרש שיפור נוסף בערימה: פעולת "הקטנת ערך" מבוצעת בזמן , בעוד שפעמים רבות פעולה זו נפוצה יותר מהאחרות ומבוצעת פעמים רבות. דוגמה לכך היא אלגוריתם דייקסטרה המשמש למציאת מסלול מינימלי בגרף ממושקל: אם בגרף יש n קודקודים ו-m קשתות, יש לשמור בערימה n איברים שייצגו את הקודקודים, ולבצע עליהם m פעולות הקטנת הערך ו-n פעולות מחיקה. משום כך זמן הריצה בערימה בינארית יהיה אך מאחר ש-m>n, היינו מעדיפים לחסוך בזמן העלות של פעולת הקטנת הערך.
ערימת פיבונאצ'י משמשת למטרה זאת. היא גמישה יותר והמבנה בה פחות קבוע ובשל כך פעולה בודדת יכולה לקחת יותר זמן מבערימה בינומית רגילה, אך יתרונה הוא בכך שהעלות לשיעורין שלה, כלומר זמן הריצה של סדרת פעולות - קטן יותר. כך לדוגמה זמן הריצה של n פעולות "הקטנת הערך", שכל אחת מהן לוקחת במקרה הגרוע, לוקח בלבד לכולן (בממוצע, לכל פעולה). וכך זמן הריצה של אלגוריתם דייקסטרה יורד ל- .
מימוש[עריכת קוד מקור | עריכה]
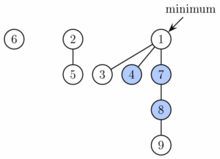
ערימת פיבונאצ'י ממומשת, בדומה לערימה בינומית, אוסף עצים. כל אחד מהעצים מקיים את "כלל הערימה" - ערך כל קודקוד לא גדול מערכי בניו. את השורשים של העצים מחזיקים ברשימה מקושרת דו כיוונית (כלומר עם מצביעים קדימה ואחורה) בנוסף שומרים מצביע לאיבר המינימלי, כדי לאפשר את החזרתו ב-.
יש מספר הגבלות שמבטיחות זמן ריצה מהיר: דרגת כל קודקוד (כלומר מספר ילדיו) היא לכל היותר , וגודל תת-עץ שדרגת השורש שלו היא k הוא לפחות כערך המספר ה-k+2 בסדרת פיבונאצ'י (ומכאן השם). כדי לשמור על כללים אלה, דואגים שאם "כורתים" שני תתי-עצים (כלומר הופכים את השורשים שלהם לעצים חדשים בערימה) כורתים גם את אביהם (אלא אם כן הוא שורש) בעזרת סימון קודקודים. שיטה זאת מבטיחה חסם תחתון על גודל העצים, אולם היא מביאה למספר גדול של עצים; כדי לתקן זאת, בפעולה "מחיקת מינימום" (שתתואר להלן) דואגים לאחד חלק מהעצים.
פעולות[עריכת קוד מקור | עריכה]



- הכנסה, מיזוג: בפעולות אלו בא לידי ביטוי המימוש ה"עצלני" של הערימה: הן ממומשות במהירות, במחיר של צעדים נוספים שידרשו לעשות פעולות אחרות. בפעולת ההכנסה פשוט מוסיפים את האיבר בהתחלה, ובפעולת המיזוג משרשרים את הערימות ליצירת ערימה שמורכבת משתיהן. פעולות אלו לוקחות .
- מחיקת מינימום: בפעולה זאת ראשית יש למחוק את האיבר המינימלי ולהפוך את ילדיו לעצים חדשים, אותם יש למזג עם הערימה. אולם, כעת יש למצוא את המינימום החדש, פעולה העלולה לקחת בזמן הגרוע . משום כך מוסיפים בפעולה זאת גם את "תיקון הערימה": מאחדים עצים בעלי דרגה זהה לעץ חדש, על ידי הוספת השורש בעל הערך הגדול יותר כבן נוסף לשורש הקטן יותר. ממשיכים בפעולה זאת עד שלא נותרים עוד שני שורשים מאותה דרגה (כדי לעשות זאת באופן יעיל, מחזיקים מערך עם מצביעים לשורשים מהדרגות השונות, ולאחר מכן עוברים על השורשים האחרים ומאחדים אותם עם הדרגה המתאימה כפי שתואר לעיל). בסופו של דבר יש למצוא את המינימום החדש - ואת זאת עושים על ידי ריצה על השורשים, ב- (מאחר שיש לכל היותר עץ אחד מכל דרגה, והדרגות גדלות באופן מעריכי כמו סדרת פיבונאצ'י).
- הקטנת ערך: בפעולה זאת מקטינים תחילה את הערך. אם הוא היה שורש, יש לבדוק האם מצביע המינימום עדיין נכון ואם לא - לתקן. אם לא, יש לבדוק האם אביו עדיין קטן ממנו או שווה לו. אם לא, "כורתים" את תת-העץ שזהו השורש שלו, כלומר הופכים אותו לעץ חדש בערימה. לאחר מכן, מסמנים את אביו (אלא אם כן הוא שורש). אם אביו כבר מסומן, גם הוא נכרת והופך לעץ חדש, ומסמנים גם את אביו. ממשיכים כך עד שמסמנים קודקוד שלא היה מסומן, או מגיעים לשורש.
- מחיקה: את המחיקה ניתן לבצע על ידי הקטנת הערך ל- (כלומר קטן יותר מכל הערכים) ולאחר מכן מחיקת המינימום.
ניתוח[עריכת קוד מקור | עריכה]
כדי לנתח את העלות לשיעורין של הפעולות, ננקוט בשיטת הפוטנציאל. פונקציית הפוטנציאל תהיה מספר העצים, ועוד פעמיים מספר האיברים המסומנים.
העלות הגרועה ביותר של פעולת מחיקת המינימום היא . נחשב את העלות לשיעורין: בפעולה היקרה ביותר, שהיא איחוד העצים, על כל איחוד עצים אנחנו מקטינים באחד את הפוטנציאל, ועל כן העלות בסופו של דבר היא (הנובע מחיפוש העצים המתאימים). עדכון המינימום גם הוא ב- ועל כן מקבלים שהעלות לשיעורין היא .
העלות הגרועה ביותר של פעולת הקטנת הערך היא . נחשב את העלות לשיעורין: נניח והיו k קודקודים שנכרתו ברצף, כלומר כולם (למעט אולי הראשון) היו מסומנים ועכשיו כבר לא, ובנוסף האבא של האחרון אולי סומן, לכן מספר המסומנים קטן במספר שבין k ל-k-2. לעומת זאת, מספר העצים גדל ב-k ולכן הפוטנציאל ירד ב-. בוצעו k פעולות. סה"כ הזמן לשיעורין הוא כלומר קבוע. לכן זמן הריצה לשיעורין הוא .
Quake Heap[עריכת קוד מקור | עריכה]
מבנה נתונים אשר משמש כחלופה לערימת פיבונאצ'י נקרא Quake Heap[2] בעל שלושת הפעולות הבאות:
- הכנסה: הכנסת איבר x אל ערימה S, פעולה זו לוקחת .
- מחיקת מינימום: מחיקת האיבר המינימלי בערימה והחזרתו, פעולה זו לוקחת .
- הקטנת ערך: שינוי ערכו של איבר מסוים לערך אשר בהכרח קטן יותר מערכו הנוכחי, פעולה זו לוקחת .
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Michal L. Fredman, Robert Endre Tarjan, Fibonacci heaps and their uses in improved network optimization algorithms
- ^ Timothy M. Chan, Quake Heaps: A Simple Alternative to Fibonacci Heaps
| מבני נתונים | ||
|---|---|---|
| מבנים מופשטים | רשימה • מחסנית • קבוצה • מולטי קבוצה • תור • דו-תור • תור עדיפויות • מילון • מחרוזת • איחוד קבוצות זרות | |
| מימושים ליניאריים | מערך • מערך משונן • טבלת גיבוב • רשימה מקושרת • רשימת דילוגים • חוצץ | |
| גרפים ועצים | ערימה (בינארית • בינומית • פיבונאצ'י) • עץ חיפוש (עץ אדום שחור • עץ 2-3 • עץ 2-3-4) • עץ סיפות • עץ B • עץ +B • עץ AVL • עץ Splay • עץ BSP • עץ kd • עץ R • Trie • טריי X מהיר • טריי y מהיר• עץ WAVL | |
| הסתברותיים | מסנן בלום | |








