גרף (תורת הגרפים)
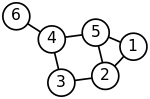

בתורת הגרפים, גרף הוא ייצוג מופשט של קבוצה של אובייקטים, כאשר כל זוג אובייקטים בקבוצה עשויים להיות מקושרים זה לזה.
האובייקטים הניתנים לקישור מכונים קודקודים או צמתים (באנגלית: vertex), וקבוצת הקודקודים מסומנת באות .
הקישורים בין הקודקודים מכונים צלעות או קשתות (באנגלית: edge), וקבוצת הצלעות מסומנת באות . מתקיים כי קבוצת הצלעות מקיימת: , כלומר: כל צלע היא זוג הקודקודים, אותם היא מקשרת (ללא חשיבות לסדר, נהוג לייצג באמצעות קבוצה).
גרף, אשר קבוצת הקודקודים שלו היא וקבוצת הצלעות שלו היא מסומן באופן הבא: .
גרפים זכו למחקר תאורטי נרחב במסגרת תורת הגרפים. הם משמשים גם לפתרון בעיות מעשיות, כגון בעיית הסוכן הנוסע, העוסקת בסוכן נוסע, שבמסגרת תפקידו עליו לעבור בערים רבות, המקושרות ביניהן ברשת כבישים, ויש למצוא את המסלול הקצר ביותר אשר מבקר בכל עיר פעם אחת בדיוק. בבעיה זו, הצמתים בגרף מייצגים את הערים, והקשתות מייצגות את הכבישים המקשרים בין הערים.
סוגי גרפים[עריכת קוד מקור | עריכה]
- גרף בלתי מכוון ולעיתים בפשטות גרף הוא קבוצה של צמתים וקבוצה של קשתות. כל קשת מקשרת בין שני צמתים. באופן פורמלי, גרף בלתי מכוון מוגדר על ידי כאשר היא קבוצת הצמתים ו־ היא קבוצת הקשתות. ניתן לראות בגרפים בלתי מכוונים מקרה פרטי של גרפים מכוונים (בהם עבור כל זוג צמתים ו־, הקשתות מ־ ל־ ומ־ ל־ קיימות שתיהן, או חסרות שתיהן).
- גרף מכוון הוא קבוצה של צמתים (גם: קודקודים או נקודות) וקבוצה של קשתות מכוונות. כאשר ישנה משמעות לכיוונה של קשת מכוונת – היא יוצאת מצומת אחד ונכנסת לצומת אחר. באופן פורמלי, גרף מכוון מוגדר על ידי כאשר היא קבוצת הצמתים ו־ היא קבוצת הקשתות. קשת יוצאת מ־ ונכנסת ל־.
- גרף תשתית של גרף מכוון הוא גרף בלתי מכוון, אשר מכיל אותה קבוצת צמתים כמו הגרף המכוון, ומכיל את הקשתות בין זוגות הצמתים אשר היו ביניהם קשתות בגרף המקורי (פורמלית, אם הוא גרף מכוון אז הוא גרף התשתית של ).
- גרף מעורב הוא קבוצה של צמתים, קבוצה של קשתות מכוונות וקבוצה של קשתות לא מכוונות. כל קשת, מכוונת או לא מכוונת, מקשרת בין שני צמתים.
- לולאה (גם: חוג עצמי) היא קשת (או קשת מכוונת) שמקשרת צומת עם עצמו.
- גרף פשוט הוא גרף לא מכוון ללא לולאות וללא קשתות מקבילות.
- גרף סופי הוא גרף שקבוצת הצמתים שלו סופית.
- גרף אינסופי הוא גרף שקבוצת הצמתים שלו היא אינסופית.
- גרף ממושקל הוא גרף שבו לכל קשת יש ערך, לרוב מספרי, המכונה משקל. באופן פורמלי, גרף ממושקל בלתי מכוון הוא שלשה , כאשר ו־ מוגדרים כמקודם, ו־ היא פונקציית המשקל מ־ לקבוצה כלשהי (למשל ).
- גרף בלתי מתויג הוא גרף שבו לא ניתן להבחין בין הצמתים. כלומר, אין אף מזהה ייחודי (כגון שם או מספר) לצומת בגרף.
תת־גרף[עריכת קוד מקור | עריכה]
תת־גרף של גרף הוא גרף המורכב משתי תתי־קבוצות של צומתי וקשתות G, דהיינו: וכן כך שהקשתות נפרשות על ידי .
או במילים אחרות: אם ו־ הם שני גרפים, אזי הוא תת־גרף של אם: וגם .
תת־גרף של גרף הוא תת־גרף מושרה אם לכל זוג של צמתים ו־ ב־, היא קשת של אם ורק אם היא קשת של . במילים אחרות, הוא תת־גרף מושרה של אם הוא מכיל את כל הקשתות של המתאימות לצמתים של ולא מכיל אף קשת נוספת.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
| נושאים בתורת הגרפים | ||
|---|---|---|
| הגדרות | צומת • קשת • דרגה • מסלול • מרחק | |
| מבנים | גרף • גרף ממושקל • מעגל • גרף מקרי • היפרגרף • מולטיגרף • עץ • קומפלקס | |
| בניות וטיפוסים | גרף משלים • גרף קיילי • גרף שלם • גרף תחרות • עץ פורש • רשת זרימה • שידוך | |
| תכונות | גרף n-צביע • גרף דו-צדדי • גרף מישורי • גרף מרחיב • גרף רגולרי • גרף קשיר • עץ בינומי • עץ פורש מינימלי | |





























