פרדוקס הסולם והאסם
פרדוקס הסולם והאסם (באנגלית: Ladder Paradox) הוא ניסוי מחשבתי המדגים כמה מן התוצאים של תורת היחסות הפרטית. הניסוי נעזר בחלק מן המסקנות של התורה כדי להביא לתוצאה שהיא לכאורה פרדוקסלית, אך מיושב שוב במסגרת התורה' באופן שממחיש את השלמות של התורה והתחזיות שלה. הניסוי נוגע לסולם, מקביל לקרקע, ולאסם שדלתותיו נסגרות ונפתחות פעם בכמה זמן. הסולם נע אופקית ולפיכך עובר התכווצות אורך. כתוצאה, הסולם מתאים בגודלו להיכנס לתוך האסם, שבמצב מנוחה יחסית היה קטן מדי בשביל להכיל אותו. מצד שני, מנקודת המבט של צופה הנמצא על הסולם, זהו האסם שנע, כך שזהו האסם שיתכווץ לגודל קטן אף יותר, ולכן לא יהיה מסוגל להכיל את הסולם.
הפרדוקס לכאורה נובע מההנחה המובלעת המוטעית של סימולטניות מוחלטת. בתורת היחסות, הסימולטניות היא יחסית לצופה, כך שבעוד בעבור מערכת ייחוס אחת שני מאורעות מתרחשים סימולטנית, במערכת הייחוס שנעה ביחס אליה מאורעות אלו מתרחשים בזמן שונה. במקרה של פרדוקס הסולם והאסם, אם במערכת המעבדה דלתות האסם נסגרות סימולטנית, במערכת הייחוס של הסולם יש הפרש זמנים קל ברגעי הסגירה והפתיחה של שתי הדלתות, כך שקיים משך זמן מסוים ששתי הדלתות פתוחות בעוד הסולם ממלא את האסם, וכך הפרדוקס נפתר, וחישוב יחסותי אכן מאשש שהדבר נכון.
תיאור הפרדוקס[עריכת קוד מקור | עריכה]



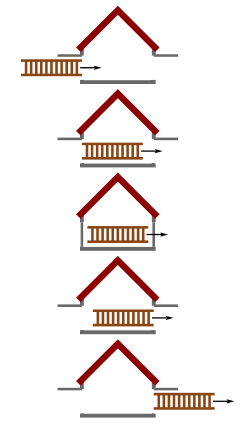
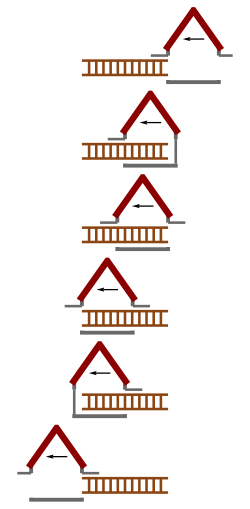
הגרסה הפשוטה ביותר של הבעיה נוגעת לאסם, עם דלת קדמית ודלת אחורית אשר פתוחות, וסולם אשר, כשהוא במנוחה יחסית לאסם, הוא ארוך מכדי להיכנס לתוכו. כעת אנו מזיזים את הסולם במהירות אופקית גבוהה דרך האסם הנייח. בגלל המהירות הגבוהה שלו, הסולם עובר את האפקט היחסותי של התכווצות האורך, ונהיה משמעותית קצר יותר. כתוצאה, כשהסולם עובר דרך האסם, הוא, למשך זמן קצר, מוכל כולו בתוך האסם. יכולנו, אם רצינו, לסגור סימולטנית את שתי הדלתות למשך זמן קצר, כדי להדגים שהסולם נמצא כולו בתוך האסם.
עד פה, התיאור עקבי. הפרדוקס לכאורה מופיע כאשר מתחשבים בסימטריה של המצב. כיוון שצופה שנע עם הסולם נע במהירות קבועה במערכת הייחוס האינרציאלית של האסם, צופה זה גם נמצא במערכת ייחוס אינרציאלית, ולכן, לפי עקרון היחסיות, אותם חוקי הפיזיקה תקפים עבורו. מנקודת המבט הזאת, הסולם הוא שכעת נייח, והאסם הוא שנע במהירות גבוהה. לכן זהו האסם שעובר התכווצות אורך, וניתן להסיק שהוא קטן בהרבה ממה שדרוש כדי להכיל במלואו את הסולם כאשר הוא (האסם) חולף על פניו: הסולם לא מתאים בגודלו, ולכן איננו יכולים לסגור את שתי הדלתות מבלי לשבור אותו. האם הסולם נשבר או לא? הסתירה לכאורה הזאת היא הפרדוקס.
פתרון הפרדוקס[עריכת קוד מקור | עריכה]
ניתוח מתמטי של הפרדוקס[עריכת קוד מקור | עריכה]
כדי להמחיש כיצד הפרדוקס נפתר באופן מלא, ניקח מקרי פרטי בו אורכו המקוצר של הסולם (שנצפה כאשר הוא נע) שווה בדיוק לאורכו של האסם. נסמן את אורך המנוחה של הסולם ב- ואת אורך המנוחה של האסם ב-. מתקיים : כאשר , כך שהסולם מתאים באורכו בדיוק לאסם. ממערכת הייחוס של הסולם, אורך האסם הוא . הסימולטניות של מאורעות הסגירה של הדלת הקדמית והאחורית (שנקרא להם מאורעות A ו-B) במערכת הייחוס של האסם לא נשמרת במעבר למערכת הייחוס של הסולם, והאינטרוול דמוי המרחב בין המאורעות A ו-B מומר בחלקו לאינטרוול דמוי זמן (עקרון שמירות האינטרוול) במערכת הייחוס של הסולם.
מטרנספורמציות לורנץ נקבל שהפרש הזמנים של המאורעות ו- (שהם מאורעות A ו-B כפי שנצפים במערכת הייחוס של הסולם) הוא . לעומת זאת הפרש הזמנים בין הרגע שבו חזית הסולם פוגשת את הדלת האחורית לרגע שזנב הסולם פוגש את הדלת הקדמית הוא : , כלומר , ובמילים אחרות במקרה פרטי זה זמני הסגירה של הדלתות מתוזמנים באופן מושלם עם זמני ההגעה של חזית הסולם.
במקרה הכללי יותר בו אורכו המקוצר של הסולם קטן מאורך האסם, השוויונות שתוארו מתורגמים לאי שוויונות שמראים באופן דומה כי הסולם לא נשבר בשתי מערכות הייחוס.
ניתוח גרפי של הפרדוקס[עריכת קוד מקור | עריכה]

את יחסיות הסימולטניות ניתן להבין גם כאילו ישרים המייצגים מאורעות סימולטניים במערכת ייחוס אחת (ישרים מקבילים לציר המקום) מיוצגים על ידי ישרים נטויים במערכת ייחוס אחרת, כמוראה בהמחשה משמאל. בפרט, אפילו הסדר של מאורעות עשוי להשתנות במעבר בין מערכת ייחוס אחת לאחרת.
הסיטואציה המוצגת בפרדוקס ניתנת להמחשה בתרשים מינקובסקי המופיע באיור למטה. התרשים הוא במערכת הייחוס של האסם. הפס הכחול האנכי מראה את האזור שהאסם תופס במרחב-זמן, והפס האדום בצורת מקבילית מראה את האזור שהסולם תופס במרחב זמן. צירי ה-x ו-t הם צירי המרחב והזמן של האסם, בהתאמה, בעוד צירי ה-'x ו- 't מייצגים את צירי המרחב והזמן של הסולם, בהתאמה. ראוי להבהיר שציר ה-t' אינו באמת מתלכד עם אחת מצלעות המקבילית, אף על פי שכך נראה באיור. בנוסף, האיור לא מתייחס למקרה המעניין ביותר בו אורכו המקוצר של הסולם שווה בדיוק לאורך האסם.
הקו האדום המודגש מקביל לציר ה-x', ומייצג את אוסף כל הנקודות (אירועים) במרחב-זמן של האסם שמתרחשות סימולטנית במערכת הייחוס של הסולם. כיוון שהקו האדום מוכל כולו בתוך המקבילית האדומה, הוא מייצג אירועים של חפיפה מרחב-זמנית של חלקי הסולם במערכת הייחוס של האסם, ולכן אם "מקבצים" את כל חלקי הסולם שנצפו במיקומים ובזמנים שונים, מקבלים למעשה את הסולם כפי שהוא נראה במערכת הייחוס של הסולם, ואורך הקו האדום המודגש הוא למעשה אורך המנוחה של הסולם (כלומר ).












