תהליך החלטה מרקובי
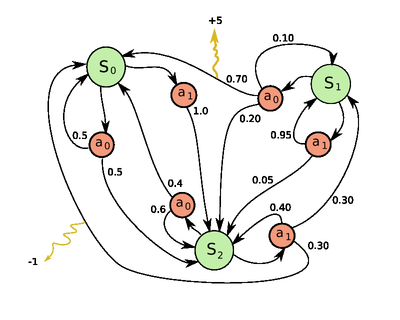
תהליך החלטה מרקובי (באנגלית: Markov Decision Process או MDP) הוא מודל מתמטי לתהליכי החלטה שבה פונקציית המעברים של המערכת מקיימת את תכונת מרקוב, קרי ההסתברות להגיע למצב כלשהו תלויה אך ורק במצב ופעולה נבחרת קודמת. המודל קרוי על שמו של אנדריי מרקוב והוא הרחבה של המודל של שרשרת מרקוב שנעשתה עם פיתוחו של ענף התכנון הדינאמי על ידי ריצ'רד בלמן בשנות ה-50 של המאה העשרים.
בצורתו הבסיסית מוגדר תהליך החלטה מרקובי באמצעות הפרמטרים כך ש:
- S הוא מרחב המצבים של המערכת.
- A הוא מרחב הפעולות.
- P היא פונקציית הסתברות למעבר בין מצבים מתוך S בהינתן ביצוע פעולה מתוך A המוגדרת
- R היא פונקציית התגמול המתאימה ערך מספרי לכל מצב (או לחלופין לכל צירוף של מצב ופעולה).
- הוא מקדם בתחום שתפקידו לקבוע עד כמה מדיניות הפעולה לגיבוש תהיה מושפעת מתגמולים שהתקבלו באינטראקציות מאוחרות בזמן.
במסגרת מודל זה, יש למצוא מדיניות פעולה כך שהתגמול הכולל לאורך זמן הניסוי עבור יהיה גבוה ככל שניתן. כדי לגבש מדיניות בחירת פעולות מתאימה תחת מודל זה, נעזרים באלגוריתמים מתחומי למידת חיזוק ובקרה אופטימלית. כמו כן קיימות גרסאות של המודל עבור מרחבי מצבים שניתנים לצפייה חלקית (Partially Observable MDP או POMDP) ועבור תהליכי החלטה לזמן רציף כשהקריטריון למיקסום הוא אינטגרל.
התהליך משמש במדעי המחשב בתחום של למידת חיזוק לשם יצירת תוכניות הלומדות לבד לפתור מערכת ולהגיע לאופטימיזציה בתהליכים בה[1].
אלגוריתמים[עריכת קוד מקור | עריכה]
קיימים אלגוריתמים שונים לפתרון בעיות של תהליך החלטה מרקובי, אלגוריתמים אלו מבוססים בדרך כלל על תכנון דינמי או על תכנון ליניארי.
בגישה של פתרון באמצעות תכנון דינמי מגדירים לרוב שני מערכים: אחד המגדיר את ערכי התגמול הממוצעים לכל מצב (), ואחד המגדיר את המדיניות () לכל מצב. ניתן להשיג פתרון באמצעות חזרה על שני השלבים הבאים:
- חישוב מדיניות:
- חישוב תגמול:
קיימות גרסאות שונות לאלגוריתם, כאשר בחלקן עוברים על כל המצבים ובחלקן עוברים על כל מצב בנפרד, או עוברים בשכיחות שונה על המצבים. דוגמאות לגרסאות נפוצות לאלגוריתם זה הן
- Value iteration - בה משלבים את חישוב המדיניות עם חישוב התגמול ומתקבל הכלל המאוחד:
- Policy iteration - בגרסה זו מחשבים את המדיניות פעם אחת, ולאחר מכן מחשבים את התגמול שוב ושוב עד להתכנסות. כאשר שלב חישוב התגמול מתכנס, מחשבים מחדש את המדיניות.


![{\displaystyle P:S{\times }S{\times }A\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc53f790348860a59632d5c123404da40b4455aa)









