אקסצנטריות (מתמטיקה)

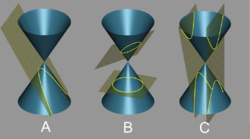
במתמטיקה, אקסצנטריות היא פרמטר המקושר עם כל חתך חרוט. ניתן לחשוב עליו כאמצעי מדידה למידת החריגה של חתך החרוט מלהיות עיגולי. בפרט,

חתכי חרוט

• האקסצנטריות של מעגל היא 0.
• האקסצנטריות של אליפסה גדולה מ- 0 וקטנה מ- 1 .
• האקסצנטריות של פרבולה היא 1.
• האקסצנטריות של היפרבולה גדולה מ- 1.
• האקסצנטריות של קו ישר היא אינסוף.

אליפסה

באליפסה, מגדירים אקסצנטריות כיחס בין מרחק המוקדים ($\ F_1$ ו- $\ F_2$) לבין הציר הראשי, כלומר: $\left ( \frac{\overline{F_1F_2}}{\overline{AB}} \right )$.

אם אורך הציר הראשי של האליפסה הוא a, ואורך הציר המשני שלה הוא b, האקסצנטריות נתונה על ידי: $e = \sqrt{1-\frac{b^2}{a^2}}$.

היפרבולה

אם אורך הציר הראשי של ההיפרבולה הוא a, ואורך הציר המשני שלה הוא b, האקסצנטריות נתונה על ידי: $e = \sqrt{1+\frac{b^2}{a^2}}$ .

קישורים חיצוניים

• אקסצנטריות (מתמטיקה), באתר MathWorld (באנגלית)