זרימה דחיסה
זרימה דחיסה היא תחום במכניקת זורמים העוסק בזורמים אשר צפיפותם משתנה באופן משמעותי, (ρ≠const), וזאת בניגוד לזרימה בלתי דחיסה שבה מניחים שצפיפות החומר קבועה. במציאות ידוע שכל זרימה ניתנת לדחיסה עד לרמה כזו או אחרת, כלומר זרימה בעלת צפיפות אחידה היא קירוב בלבד, אולם עבור רוב הזרימות שמערבות נוזלים, כמו גם זרימות של גזים תחת תנאים מסוימים, השינויים בצפיפות כל כך קטנים כך שניתן להניח שהצפיפות נשארת קבועה.
תופעות של דחיסות בדרך כלל נחשבות כמשמעותיות אם מספר מאך עולה על 0.3, או אם הזורם נמצא תחת שינויי לחץ משמעותיים. תופעות בולטות המתרחשות בזרימה דחיסה הן זרימה חנוקה (Choked flow) והנוכחות של גלים אקוסטיים, המכונים גם גלי התפשטות או גלי התכנסות, תלוי אם הם גורמים לעלייה או לירידה בלחץ. כמו כן מודלים של זרימה דחיסה מאפשרים את קיומם של גלי הלם.
הגדרה[עריכת קוד מקור | עריכה]
זרימת דחיסה מתארת את התנהגותם של נוזלים אשר חווים שינויים משמעותיים בצפיפות. עבור כל זורם הצפיפות אינה קבועה, אך עבור זורמים שבהם הצפיפות אינה משתנה באופן משמעותי אנו מבצעים "אידיאליזציה" אשר מובילה לתאוריה של זרימה בלתי דחיסה, אשר לעיתים פשוטה בהרבה מהתאוריה של זרימה דחיסה. עם זאת, במקרים רבים העוסקים בגזים (במיוחד במהירויות גבוהות) ובמקרים העוסקים בנוזלים עם שינויים גדולים בלחץ, שינויים משמעותיים בצפיפות יכולים להתרחש, וכדי להשיג תוצאות מדויקות יש לנתח את הזרימה כזרימה דחיסה.
כאשר מתחשבים בשינויי הצפיפות, מכניסים עוד משתנה למערכת -צפיפות. זאת בניגוד לזרימה לא דחיסה אשר בדרך כלל ניתן לפתור עם משוואת התנע, משוואת שימור המסה, ומשוואת האנרגיה. כאן יש להכניס משוואה נוספת למערכת, כדוגמת משוואת הגזים האידיאליים.
גלי הלם[עריכת קוד מקור | עריכה]
גלי הלם הם אחת הדוגמאות הנפוצות ביותר של זרימת דחיסה. גל הלם מאופיין בקפיצת אי-רציפות בתכונות תרמודינמיות לפני ואחרי הגל. עבור זרימה חד־ממדית, גלי הלם יכולים להיווצר כאשר סדרה של גלי התכנסות מתנגשים, או כאשר קרום המפריד בין שני אזורי לחץ שונים הוסר לפתע. זוהי הטכניקה המשמשת לעיתים קרובות כדי לייצר גלי הלם בצינורות הלם (Shock Tubes). בזרימה דו-ממדית ותלת-ממדית, גלי הלם אלכסוניים יכולים להתרחש כתוצאה משינויים בכיוון הזרימה. דוגמה קלאסית של גלי הלם הן אלו שנוצרים על אף של מטוס הטס במהירות על קולית.
זרימה דחיסה חד־ממדית[עריכת קוד מקור | עריכה]
 ערך מורחב – זרימה דחיסה חד-ממדית
ערך מורחב – זרימה דחיסה חד-ממדית
משוואות איזנטרופיות עבור זרימה דחיסה[עריכת קוד מקור | עריכה]
המשוואות האיזנטרופיות מתארות את היחס בין הפרמטרים של זרימה איזנטרופית לאורך קו זרם, כתלות במספר המאך (M). כלומר, עבור מספר מאך נתון ניתן למצוא את הפרמטרים כגון צפיפות, טמפרטורה, לחץ ומהירות הקול, כתלות בערך הסטגנציה שלהם- הערך שבו הגז נמצא במנוחה ומהירותו שווה ל-0. כל מה שנותר לעשות כדי לקבל את הפרמטרים זה למצוא את הערך של הזורם במצב של מנוחה, ולחלץ את הפרמטרים מהמשוואות האיזנטרופיות. זרימה דחיסה איזנטרופית (בעלת אנטרופיה קבועה, S=const) מאופיינת על ידי המשוואות הבאות:
טמפרטורה:
מהירות הקול בחתך:
צפיפות בחתך:
לחץ בחתך:
- - מס' מאך,
- - אינדקס אדיאבטי
- - טמפ', - טמפ' במצב סטגנציה (v=0)
- - מהירות הקול, - מהירות הקול במצב סטגנציה
- - צפיפות, - צפיפות במצב סטגנציה
- - לחץ, - לחץ במצב סטגנציה
זרימה דו־ממדית[עריכת קוד מקור | עריכה]
למרות שניתן לבצע ישירות אנליזה אנליטית עבור זרימה חד־ממדית, זאת רק מקרה פרטי של זרימה דו־ממדית. מכאן נובע כי אחת התופעות המאפינות של זרימה חד־ממדית, גל הלם ניצב, הוא גם רק מקרה פרטי השייך לקבוצה גדולה יותר של גלי הלם משופעים. גלי הלם משופעים הם הרבה יותר נפוצים ביישומים כגון: עיצוב אף של מטוסים, חפצים בטיסה על־קולית, וברמה בסיסית יותר נחירים ודיפיוזרים על־קוליים. בהתאם לתנאי הזרימה, גל הלם משופע יהיה מחובר או מופרד מהזרימה בצורה של גל הלם ניצב- BOW SHOCK.

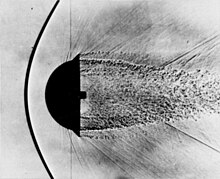
גלי הלם משופעים[עריכת קוד מקור | עריכה]
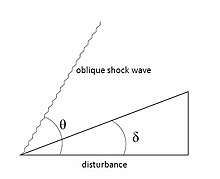
גלי הלם משופעים דומים לגלי הלם ניצבים, אבל הם מתרחשים בזוויות קטנות מ-90 מעלות עם כיוון הזרימה. כאשר הפרעה לזרימה מופיע בזווית שונה מאפסת (δ), הזרימה חייבת להגיב לתנאי השפה משתנים. לכן גל הלם משופע נוצר, וכתוצאה מכך משנה את כיוון הזרימה.
דיאגרמה פולרית של גל הלם[עריכת קוד מקור | עריכה]

עוצמת גלי ההלם המשופעים תלויה ברמת סטיית הזרימה δ. גלי הלם חזקים מאופיינים בסטייה מכיוון הזרימה המקורי ואובדן אנטרופיה גדולה יותר על פני גל ההלם מפני גלי הלם חלשים. על מנת להגיע לתובנה מהירה לגדלים אלו, ניתן להשתמש בדיאגרמה פולרית של הלם. עם הטמפרטורה הסטטית אחרי גל הלם, *T, ידוע אזי מהירות הקול אחרי הגל מוגדרת:
כאשר R קבוע הגזים ו- הוא יחס החום סגולי.
שדה הזרימה דו־ממדי ולכן ניתן לחלק את מספרי המאך לקואורדינטאות קרטזיות:
כאשר ו- הם הקואורדינטות בכיוון x ו-y של מהירות הזורם בהתאמה. כאשר מספר המאך לפני גל ההלם נתונה ניתן לחלץ מספר פרמטרים. עבור δmax הזרימה עוברת מגל הלם משופע חזק לחלש. ועבור δ = 0° נוצר גל הלם ניצב.
שיקוף של גל הלם משפוע[עריכת קוד מקור | עריכה]
כתוצאה מכיוון של גל ההלם, לאחר שגל הלם משופע נוצר, הוא יכול לקיים אינטראקציה עם גבול בשלושה באופנים שונים, הסבר של שני אופנים מוצג למטה.
גבול אחיד[עריכת קוד מקור | עריכה]
זרימה נכנסת במקביל לגבול אחיד ומוסטת ב- זווית δ על ידי הפרעה. גל ההלם משתקף מהגבול האחיד, והזרימה מוסטת שנית בזווית כדי שוב לזרום במקביל לגבול. חשוב לציין כי כל גל הלם עוקב מתחלש וזווית הגל גדלה.
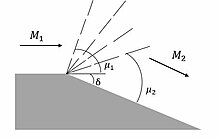
שיקוף אסימטרי[עריכת קוד מקור | עריכה]
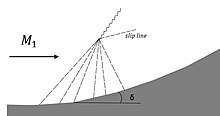
שיקוף אסימטרי הוא כמה המקרה המוצג לעיל רק שהפעם הרבה יותר גדול מזווית הסטייה המקסימלית. כתוצאה מכך גל הלם מנותק נוצר והשתקפות הרבה יותר מורכבת מתרחשת.
מניפות מתפשטות[עריכת קוד מקור | עריכה]
עד לשלב זה, תופעות הזרימה שהוזכרו הם גלי הלם, אשר מאטים את הזרימה ומגדילים את האנטרופיה שלה. ניתן להאיץ זרימה על־קולית על ידי מה שמכונה מניפה פרנדט-מאייר מתפשטת על שם לודוויג פרנדט ותיאדור מאייר. אופן ההתפשטות מוצג באיור משמאל.
מניפות פרנדט-מאייר[עריכת קוד מקור | עריכה]
ניתן לבטא מניפות פרנדט-מאייר כמניפות מתפשטות ומתכנסות ויכולים גם לחצות שכבות גבול אשר גם כן גורם לשינויים בשדה הזרימה. כאשר גל הלם פוגעת בגוף קשיח הוא המניפה הנוצרת או כהלם שמתכנס או כמניפה שמתפשטת בניגוד לסוג גל ההלם שפגע.
בניגוד לזרימת בא נתקלים במכשול קעור ומייצר גל הלם משופע, הזרימה מתרחבת מעבר לפינה קמורה ומהווה מניפה מתפשטת באמצעות סדרה של גלי מאך איזנטרופים. המניפה הנוצרת מורכבת מגלי מאך המתפרשים מזווית מאך ההתחלתית לזווית מאך הסופית. הזורם יכול להתרחב סביב פינה חדה או מעוגלת במידה שווה, והגידול במספר מאך פורפוציונלי לזווית הקמורה של הקטע (δ). הפינה המרחיבה שמייצרת את מניפת פרנדט-מאייר יכולה להיות חדה (כפי שמודגם באיור) או מעוגלת. אם זווית המניפה הכולל זהה,
אז גם פתרון זרימת ה-P-M (פרנדט-מאייר) זהה.
מניפת פרנדט-מאייר מתכנסת[עריכת קוד מקור | עריכה]
מניפת פרנדט-המאייר מתכנסת היא התופעה ההפוכה למניפת פרנדט-מאייר מתפשטת. אם הזרימה מוסטת בהדרגה דרך מחסום בזווית של δ, מניפה מתכנסת יכולה להיוצר. מניפה זו מהווה סדרה של גלי מאך שבסופו של דבר מתגבשים לגל הלם משופע. מכיוון שהזרימה מוגדרת על ידי אזור איזנטרופי (הזרימה שעוברת דרך מניפה) וכן על ידי אזור לא איזנטרופי (זרימה שעוברת דרך גל הלם משופע), נוצר קו החלקה בין שני אזורי הזרימה.
זרימה בנחיר אדיאבטי מתכנס[עריכת קוד מקור | עריכה]
נחיר מתכנס הוא מתקן שככל שמתקדמים לאורכו כך קטן שטח החתך שלו. משתמשים בנחיר מתכנס על מנת להגביר את מהירותו של הזורם על ידי יצירת "מפל-לחץ"- הפרש לחצים בין הכניסה ליציאה מהנחיר שגורם להגברת מהירות הזורם ובכך להגברת הספיקה המסית . זרימה דחיסה היא בעלת משמעות חשובה לגבי ההתנהגות של הזורם בנחיר, ומגיבה שונה לשינויים בשטח החתך כאשר הזורם הדחיס נע במהירות על-קולית או תת-קולית. בעוד שזרימה תת-קולית הזורמת דרך צינור מתכנס (הקוטר של הצינור משתנה מרחב יותר לצר יותר עם כיוון הזרימה) חווה עלייה במהירות, זרימה על-קולית דרך צינור זהה תחווה ירידה במהירות.
ערכים קריטיים (M=1)[עריכת קוד מקור | עריכה]
הערכים הקריטיים מתקבלים עבור מס' מאך השווה ל-1 (M=1), ויסומנו על ידי כוכבית (*) כך לדוגמה הלחץ הקריטי יסומן על ידי .
זרימה חנוקה[עריכת קוד מקור | עריכה]
זרימה חנוקה היא זרימת אשר משויכת לזרימה דחיסה, כאשר הפרמטר שהופך להיות "נחנק" או "מוגבל" הוא קצב זרימת המסה (ספיקה מסית) .
כאשר זורם דחיס (לדוגמה: אוויר), הזורם בלחץ ומהירות מסוימים, עובר דרך הגבלה (כמו נחיר אדיאבטי מתכנס או שסתום בצינור) הלחץ אליו הוא עובר קטן ואילו המהירות גדלה. עבור זרימה איזנטרופית אנו יודעים גם כי כלומר ניתן לראות שלמהירות הזרימה יש ערך עליון Vmax שאותו לא ניתן לעבור, ובעקבותיו גם יש הגבלה על הספיקה המסית. זרימה חנוקה היא מצב מגביל שמשמעותו שיש "רף עליון" עבור הספיקה המסית, ואפילו אם נמשיך ונגדיל את היחס בין הלחץ לפני הנחיר לעומת הלחץ מחוץ לנחיר , עדיין הספיקה המסית לא תשתנה.
יש להבדיל בין 2 מקרים:
- : במצב זה מתקבלת זרימה תת-קולית ביציאה מהנחיר, והלחץ ביציאה יהיה .
- : זוהי זרימה חנוקה. במצב זה מהירות היציאה מהנחיר היא מהירות הקול, והלחץ ביציאה הוא הלחץ הקריטי .
משוואות אקוסטיות[עריכת קוד מקור | עריכה]
המשוואות האקוסטיות מתארות את הקשרים המתמטיים הקיימים עקב הפרעות בזרימה דחיסה. במצב של בוכנה שנעה קדימה, ניתן לראות איך ההפרעות הנוצרות בזרימה כתוצאה מתנועת הבוכנה משפיעות על הצפיפות והלחץ בחומר הדחיס.
הנחות[עריכת קוד מקור | עריכה]
- תנועה חד-ממדית
- למהירות רק רכיב בכיוון האופקי
- הגז היה בהתחלה במצב של מנוחה, ללא הפרעות.
- בזרימה נוצרות הפרעות וכתוצאה מכך משתנים הלחץ המהירות והצפיפות:
- הם ההפרעה במהירות, בצפיפות ובלחץ, והם קטנים מאוד ביחס למהירות הקול, לצפיפות ההתחלתית והלחץ ההתחלתי בהתאמה.
המשוואות האקוסטיות[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Shapiro, Ascher H. (1953). The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press. ISBN 978-0-471-06691-0.
- Anderson, John D. (2004). Modern Compressible Flow. McGraw-Hill. ISBN 0-07-124136-1.
- Liepmann, H. W.; Roshko A. (2002). Elements of Gasdynamics. Dover Publications. ISBN 0-486-41963-0.
- von Mises, Richard (2004). Mathematical Theory of Compressible Fluid Flow. Dover Publications. ISBN 0-486-43941-0.
- Meyer, Richard E. (2007). Introduction to Mathematical Fluid Dynamics. Dover Publications. ISBN 0-486-45887-3.
- Saad, Michael A. (1985). Compressible Fluid Flow. Prentice Hall. ISBN 0-13-163486-0.
- Schreier, S. (1982). Compressible Flow. Wiley-Interscience. ISBN 0-471-05691-X.
- Lakshminarayana, B. (1995). Fluid Dynamics and Heat Transfer of Turbomachinery. Wiley-Interscience. ISBN 978-0-471-85546-0.


























![{\displaystyle {\frac {A_{0}}{A^{*}}}={\frac {1}{M}}[({\frac {2}{\gamma +1}})(1+{\frac {\gamma -1}{2}}M^{2})]^{\frac {\gamma +1}{2(\gamma -1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb9deea52be6a7f672422003c6a872ab8b6da517)










