זרימת פאנו
זרימת פאנו - זרימה אדיאבטית דרך תעלה בעלת שטח קבוע עם התייחסות להשפעת החיכוך.[1] לעיתים קרובות השפעת הדחיסות תילקח בחשבון ,אף על פי שמודל זרימת הפאנו בהחלט תקף גם לזרימה בלתי דחיסה. לצורך מודל זה מניחים כי שטח התעלה נשאר קבוע, הזרימה תמידית וחד־ממדית, ואין מסה שמתווספת לאורך התעלה. מודל זרימת הפאנו נחשב לתהליך בלתי הפיך עקב אפקט הוויסקוזיות (צמיגות).החיכוך הוויסקוזי (צמיגי) גורם לתכונות הזרימה להשתנות לאורך התעלה. השפעת החיכוך ממודלת כלחץ גזירה על דפנות התעלה ופועלת על הנוזל בתכונות אחידות לאורך כל חלק בתעלה. עבור זרימה עם מספר מאך הגדול מ 1.0 בתעלה ארוכה דיה, מתרחשת האטה והזרימה עלולה להיחנק (עלולה להתבצע תופעת החניקה). מאידך, עבור זרימה עם מספר מאך הקטן מ 1.0, תתרחש ההאצה והזרימה עלולה להיחנק בתעלה ארוכה דיה. ניתן להראות כי עבור זרימה של גז מושלם קלורית האנטרופיה המקסימלית מתרחשת כאשר מספר מאך שווה ל 1. זרימת פאנו קרויה על שם ג'ינו ג'ירולאמו פאנו ( Gino Girolamo Fanno).
תאוריה[עריכת קוד מקור | עריכה]
מודל זרימת הפאנו מתחיל במשוואה דיפרנציאלית שמקשרת בין השינוי במספר מאך לאורך התעלה,dM/dx. תנאים נוספים במשוואה הדיפרנציאלית הם יחס קיבולי החום, γ, מקדם החיכוך של פאנינג ,f והקוטר ההידראוליDh:
בהנחה שמקדם החיכוך של פאנינג קבוע לאורך כל קירות התעלה, המשוואה הדיפרנציאלית יכולה להיפתר בקלות..[2][3] לעומת זאת חשוב לזכור שהערך של מקדם חיכוך פאנינג עלול להיות קשה לקביעה במהירויות זרימה על-קוליות והיפר-קוליות. את תוצאת היחס ניתן לראות מטה כאשר L* הוא אורך התעלה הדרוש לחניקת הזרימה בהנחה שמאך הזרם סופר-סוני. צידה השמאלי של המשוואה נקראה קבוע פאנו
:
חשוב במידה שווה למודל זרימת פאנו הוא היחס חסר הממדים של: השינוי באנטרופיה ביחס לקיבול החום בלחץ קבוע, cp.
:
המשוואה מעלה יכולה להירשם מחדש בתנאים סטטיים ליחס טמפרטורת העצירה (סטגנציה), שעבור גז מושלם קלורית שווה ליחס אנתלפיה חסר ממד, H:
:
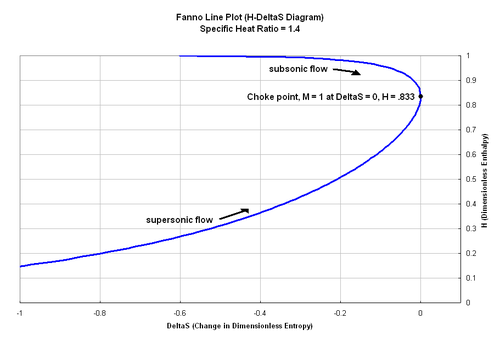
במשוואה מעלה ניתן להשתמש כדי לשרטט את קו פאנו, המיצג אוסף מצבים לתנאי זרימת פאנו על דיאגרמת H-ΔS.בדיאגרמה, קו פאנו מגיעה לאנטרופיה מרבית כאשרH = 0.833 והזרימה נחנקת. בהתאם לחוק השני של התרמודינמיקה, אנטרופיה לעולם תתגבר עבור זרימת פאנו. משמעות עובדה זו היא שזרימה תת-קולית הנכנסת לתעלה עם חיכוך מספר המאך יעלה עד לחנק הזרימה. מנגד, מספר המאך של זרימה על קולית יקטן עד שהזרימה תיחנק. כל נקודה על קו פאנו מתאימה למספר מאך אחר, והתנועה לחניקת הזרימה מוצגת בדיאגרמה. קו פאנו מגדיר את המצבים האפשריים עבור גז כאשר קצב זרימת המסה וסכום האנתלפיה נחשבים לקבועים, אך המומנטום משתנה. לכל נקודה על קו פאנו ערך מומנטום שונה, ואת השינוי במומנטום ניתן לייחס להשפעת החיכוך[4].
יחסים נוספים של זרימת פאנו[עריכת קוד מקור | עריכה]
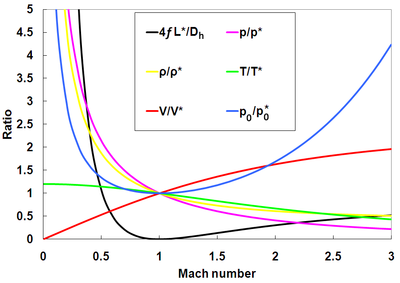
כפי שצוין קודם לכן, השטח ויחס זרימת המסה בתעלה נחשבים לקבועים בזרימת פאנו. נוסף על כן, טמפרטורת הסטגנציה נותרת קבועה. יחסים אלו ניתן לראות מטה כאשר הסימן * מייצג את נקודת צוואר הבקבוק, היכן שיכולה להיווצר החניקה. תכונת הסטגנציה מכילה מיוצגת על ידי האינדקס 0.
:
ניתן לפתח ולפתור משוואות דיפרנציאליות כדי לתאר יחסי תכונת זרימת פאנו בהתחשב בערכים בנקודות החניקה. היחסים עבור לחץ, צפיפות, טמפרטורה, מהירות ולחץ הסטגנציה מוצגים מטה בהתאמה. אלו מיוצגים בצורה גרפית בנוסף לקבוע פאנו .
:
יישומים[עריכת קוד מקור | עריכה]



במודל זרימת הפאנו נעשה שימוש לעיתים קרובות בתיכון וניתוח של נחירים. בנחיר השטח המתכנס או המתפזר ממודל עם זרימה איזנטרופית, בעוד שחלק השטח הקבוע שלאחר מכן ממודל בזרימת פאנו. עבור תנאי זרם נתונים בנקודה 1 כפי שמוצג באיורים 3 ו4 ניתן לבצע חישובים לקביעת מספר המאך בעת יציאה מהנחיר ואת מיקום גל הלם ניצב באזור השטח הקבוע בתעלה. נקודה 2 מתארת את צוואר הבקבוק של הנחיר, היכן ש M = 1 במידה והזרימה חניקה. נקודה 3 מציינת את סוף הנחיר היכן שהזרימה הופכת מזרימה איזנטרופית לזרימת פאנו. אם לחץ התחלתי גבוה דיו, ניתן לשמר זרימה על קולית בקטע התעלה בעל השטח הקבוע, בדומה לביצוע הנדרש ממנהרת רוח על קולית מסוג BLOWDOWN . לעומת זאת, איורים הלו מציגים את גל ההלם תרם עבר לאורך התעלה בשלמותו. אם גל ההלם קיים, תיאור הזרימה על קו הפאנו ישתנה מהחלק העל קולי לחלק התת-קולי לפני שהזרימה תמשיך לעבר M = 1. התנועה באיור 4 לעולם תהיה משמאל לימין על מנת לספק את החוק השני של התרמודינמיקה. מודל זרימת הפאנו בא לידי שימוש בצורה נרחבת גם עם מודל זרימת ריילי. שני מודלים אלו נחתכים בנקודות על עקומות האנתלפיה-אנטרופיה (h-s) ומספר מאך-אנטרופיה (M-h) ,עובדה משמעותית ביותר ביישומים רבים. לעומת זאת ערכי האנטרופיה עבור כל מודל אינם שווים במצב הקולי. השינוי באנטרופיה הוא 0 כאשר M = 1 עבור כל אחד מהמודלים, אך משמעות ההצהרה הקודמת היא שהשינוי באנטרופיה עבור מנקודה שרירותית אל הנקודה הקולית שונה עבור מודלי זרימת פאנו וריילי. אם הערכים ההתחלתיים של si ו Mi מוגדרים, ניתן להגדיר עבור כל אחד מהמודלים משוואה חדשה עבור אנטרופיה חסרת ממד אל מול מספר מאך. משוואות אלו מוצגות מטה עבור זרימות פאנו וריילי בהתאמה :
:
באיור 5 מוצגים קווי פאנו וריילי הנחתכים עבור תנאי התחלה : si = 0 וMi = 3. נקודות החיתוך מחושבות על ידי השוואה בין משוואות האנטרופיה חסרות הממד החדשות ( ), התוצאה מוצגת במשוואה מטה.
מעניין לצפות כי, נקודות החיתוך מתרחשות במספר המאך ההתחלתי ובערך ההלם הפוסט נורמלי שלו. עבור איור 5, ערכים הלו הם M = 3 ו M=0.4752 .כפי שניתן למצוא בטבלאות גלי ההלם הנורמליים הנמצאות ברוב ספרי הלימוד של זרימה דחיסה. זרם נתון עם שטח תעלה קבוע יכול לעבור בין מודל פאנו למודל ריילי בנקודות אלו.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- Purdue University Adiabatic and Isothermal Fanno flow calculators
- University of Kentucky Fanno flow Webcalculator
- Maurice W. Downey, Gino Fanno
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Shapiro, A.H., The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1, Ronald Press, 1953.
- ^ Zucker, R.D., Biblarz, O., Fundamentals of Gas Dynamics, John Wiley & Sons, 2002.
- ^ Hodge, B.K., and Koenig, K., Compressible Fluid Dynamics with Personal Computer Applications, Prentice Hall, 1995.
- ^ The Phenomena of Fluid Motions, R. S. Brodkey, p187, R. S. Brodkey (pub), 1995


![{\displaystyle \ {\frac {4fL^{*}}{D_{h}}}=\left({\frac {1-M^{2}}{\gamma M^{2}}}\right)+\left({\frac {\gamma +1}{2\gamma }}\right)\ln \left[{\frac {M^{2}}{\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d3400a03fe159951756769bd5df8f2607a20b8)
![{\displaystyle \ \Delta S={\frac {\Delta s}{c_{p}}}=\ln \left[M^{\frac {\gamma -1}{\gamma }}\left(\left[{\frac {2}{\gamma +1}}\right]\left[1+{\frac {\gamma -1}{2}}M^{2}\right]\right)^{\frac {-(\gamma +1)}{2\gamma }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c679a2d173adae85d4f6436444b15048ec999f8b)

![{\displaystyle \ \Delta S={\frac {\Delta s}{c_{p}}}=\ln \left[\left({\frac {1}{H}}-1\right)^{\frac {\gamma -1}{2\gamma }}\left({\frac {2}{\gamma -1}}\right)^{\frac {\gamma -1}{2\gamma }}\left({\frac {\gamma +1}{2}}\right)^{\frac {\gamma +1}{2\gamma }}\left(H\right)^{\frac {\gamma +1}{2\gamma }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dab1f349013744ebcf2e6ceefa006a98f85ee8b)

![{\displaystyle {\begin{aligned}{\frac {p}{p^{*}}}&={\frac {1}{M}}{\frac {1}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}}\\{\frac {\rho }{\rho ^{*}}}&={\frac {1}{M}}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\\{\frac {T}{T^{*}}}&={\frac {1}{\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}\\{\frac {V}{V^{*}}}&=M{\frac {1}{\sqrt {\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)}}}\\{\frac {p_{0}}{p_{0}^{*}}}&={\frac {1}{M}}\left[\left({\frac {2}{\gamma +1}}\right)\left(1+{\frac {\gamma -1}{2}}M^{2}\right)\right]^{\frac {\gamma +1}{2\left(\gamma -1\right)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caf30572891bf439a34e222c067d4f14b8e76ab0)
![{\displaystyle {\begin{aligned}\Delta S_{F}&={\frac {s-s_{i}}{c_{p}}}=\ln \left[\left({\frac {M}{M_{i}}}\right)^{\frac {\gamma -1}{\gamma }}\left({\frac {1+{\frac {\gamma -1}{2}}M_{i}^{2}}{1+{\frac {\gamma -1}{2}}M^{2}}}\right)^{\frac {\gamma +1}{2\gamma }}\right]\\\Delta S_{R}&={\frac {s-s_{i}}{c_{p}}}=\ln \left[\left({\frac {M}{M_{i}}}\right)^{2}\left({\frac {1+\gamma M_{i}^{2}}{1+\gamma M^{2}}}\right)^{\frac {\gamma +1}{\gamma }}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31b696ced22bb1df158e11d46ce5b9f5a19b64b5)
![{\displaystyle \ \left(1+{\frac {\gamma -1}{2}}M_{i}^{2}\right)\left[{\frac {M_{i}^{2}}{\left(1+\gamma M_{i}^{2}\right)^{2}}}\right]=\left(1+{\frac {\gamma -1}{2}}M^{2}\right)\left[{\frac {M^{2}}{\left(1+\gamma M^{2}\right)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1031340758891c29e5707e01def7e1c5983b548d)