חוק הפילוג
במתמטיקה ובעיקר באלגברה, חוק הפילוג הוא תכונה של פעולות בינאריות, שמכלילה את חוק הפילוג של החיבור והכפל המוכר מאריתמטיקה.
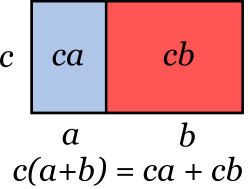
ניתן לראות דוגמה לתכונה זו במשוואה הבאה:
כאן באגף שמאל של המשוואה, 4 מוכפל בסכום של שני מספרים, 3 ו-2. לעומת זאת, בצד ימין 4 מוכפל בכל אחד מהאיברים בנפרד, ואת התוצאות מחברים. מכיוון שבשתי הדרכים מתקבלת אותה התוצאה, ולא משנה איזה מספרים יוצבו במשוואה, אומרים במקרה זה כי חוק הפילוג תקף, או כי הכפל דיסטריבוטיבי מעל החיבור.
נשים לב שהדבר אינו תמיד נכון לכל שתי פעולות בינאריות, למשל:
- .
כאן באגף שמאל התוצאה המתקבלת היא 10, ואילו באגף ימין מתקבל 42. על כן החיבור אינו דיסטריבוטיבי מעל הכפל.
הגדרה פורמלית[עריכת קוד מקור | עריכה]
תהא קבוצה ויהיו שתי פעולות בינאריות המוגדרות עליה. נאמר כי:
- הוא דיסטריבוטיבי משמאל מעל אם לכל מתקיים .
- הוא דיסטריבוטיבי מימין מעל אם לכל מתקיים .
- הוא דיסטריבוטיבי מעל אם הוא דיסטריבוטיבי מימין ומשמאל מעליו.
אם היא פעולה קומוטטיבית הרי ששלושת התנאים הללו שקולים.
דוגמאות[עריכת קוד מקור | עריכה]
- הכפל מתפלג מעל החיבור, וכן מעל החיסור. החילוק מתפלג מעל שתי הפעולות הנ"ל מימין.
- החזקה מתפלגת משמאל מעל הכפל.
- האיחוד והחיתוך מתפלגים זה מעל זה.
- באלגברה בוליאנית, פעולות ה"וגם" וה"או" מתפלגות זו מעל זו.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- חוק הפילוג, באתר MathWorld (באנגלית)









