משפט מנלאוס
מראה
בגאומטריה אוקלידית, משפט מנלאוס נותן תנאי הכרחי ומספיק לכך ששלוש נקודות על צלעות משולש או המשכיהן תהיינה מונחות על ישר אחד.
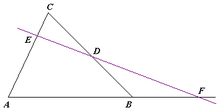

המשפט קובע (לפי הסימונים שבשרטוטים בצד שמאל) שהנקודות D,E,F על ישר אחד (בשרטוט - הישר הסגול) אם ורק אם מתקיים: (כאשר היחסים מסומנים על-פי הכיוון).
הוכחה
[עריכת קוד מקור | עריכה]נטיל את שלוש הנקודות לישר המאונך לישר DE; נסמן כל נקודה בהיטל באות של הנקודה המקורית עם תג ('). על-פי משפט תאלס, משפט מנלאוס שאנו רוצים להוכיח שקול לקביעה ש-D' ו-F' מתלכדות אם ורק אם: , ונוסחה זו שקולה ל , השקולה ל- . ברור שזה מתקיים אם ורק אם D',ו-F' מתלכדות.
ראו גם
[עריכת קוד מקור | עריכה]קישורים חיצוניים
[עריכת קוד מקור | עריכה]- משפט מנלאוס, באתר MathWorld (באנגלית)




