משתמשת:Ilor94/משפט טיילור

הפונקציה המעריכית y = e^x (העקומה באדום) ובמקביל פולינום טיילור שלו (המקווקו בירוק).

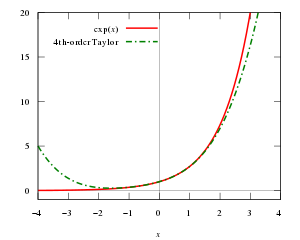
בחשבון דיפרנציאלי ואינטגרלי טיילור הוא משפט שנותן קירוב של פונקציה שגזירה k פעמים סביב נקודה מסוימת. קירוב זה נקרא פולינום טיילור

משפט טיילור קרוי על שם המתמטיקאי ברוק טיילור, אשר מצא את הגרסא הראשונה שלו בשנת 1712. באותם זמנים עדיין לא מצאו ביטוי מפורש לשגיאה, זה קרה מאוחר הרבה יותר על ידי ג 'וזף-לואי לגראנז'. גרסה מוקדמת יותר של התוצאה כבר הוזכרה בשנת 1671 על ידי ג ' יימס גרגורי.

משפט טיילור נלמד בקורסי מבוא במתמטיקה, וזה אחד המשפטים המרכזיים באנליזה מתמטית. במתמטיקה טהורה הוא נקודת המוצא של יותר כלים יותר מתקדמים כמו ניתוח איסמפטוטי, ומשולב במספרים נומרים בפיזיקה מתמטית. טיילור זה משפט שניתן להכליל גם לפונקציות רבות משתנים- פונקציות ${\displaystyle }$משפט זה הוא בסיס התאוריה של מה שנקרא מטוסים אשר מופיעים בגיאומטריה משתנה ובמשוואות דיפרנציאליות חלקיות.

מוטיבציה

הגרף של f(x) = e^x (כחול) עם קירוב ליניארי P₁(x) = 1 + x (אדום) ב- a=0.

       

  משום שפונקציה f גזירה בנקודה, יש לה קירוב לינארי בנקודה. משמעות הדבר היא שקיימת פונקציה h₁ מהצורה- 

${\displaystyle }$

לכן,

${\displaystyle }$

זה הקירוב הליניארי של  f בנקודה. הגרף של y=P1(x) הוא קו משיק על הגרף של f ב - x = a.      השגיאה בקירוב היא:

${\displaystyle }$

(שימו לב כי זה שואף לאפס קצת יותר מהר מאשר x − a)

הגרף של f(x)=e^x (כחול) עם הקירוב הריבועי של P₂(x) = 1 + x + x²/2 (אדום) ב - a = 0. נראה שיפור בקירוב.

אם אנחנו רוצים קירוב טוב יותר ל f, ניתן לנסות פולינום ריבועי במקום פונקציה לינארית. במקום לגזור את f רק פעם אחת ניתן לגזור את f יותר פעמים. למשל,

${\displaystyle }$

משפט טיילור זה משפט מבטיח קירוב ע"י פונקציה ריבועית בסביבה מנוקבת של הנקודה a, הוא הערכה טובה יותר מאשר הקירוב הלינארי. באופן ספציפי,

${\displaystyle }$

כאשר כאן שגיאת קירוב היא-

${\displaystyle }$

בהתחשב בכך שהגבול של h2 שואף מהר יותר ל0 מאשר ${\displaystyle }$

קירוב של f(x) = 1/(1 + x²) על פי פולינומי טיילור  P_k מסדר k = 1, ..., 16 סביב הנקודה x = 0 (אדום), x = 1 (ירוק). את הקירובים לא ניתן לשפר בכלל מחוץ לקטעים                       (1,1-) ו- (2√+2,1√-1) בהתאמה.

באופן דומה, נוכל לקבל קירובים טובים יותר ל -  f אם נשתמש בפולינומים מדרגה גבוהה יותר, שכן אז אנחנו יכולים להתאים אפילו יותר נגזרות ל f בנקודה מסויימת.

באופן כללי, שגיאת הקירוב של הפונקציה על-ידי פולינום מדרגה k תשאף לאפס מהר יותר מ- (x − a)^k כאשר x שואף ל a. אך זה לא תמיד קורה: יתכן מצב שנגדיל את דרגת הפולינום אך איכות הקירוב לא משתפר אפילו אם הפונקציה גזירה אינסוף פעמים. דוגמה להתנהגות כזאת ניתנת בהמשך, והיא קשורה לעובדה כי ישנם פונקציות כלליות  אבל אולי זה לא תמיד המקרה: זה גם אפשרי, כי הגדלת מידת הקירבה פולינום לא להגדיל את האיכות של קירוב כלל אפילו אם הפונקציה f כדי להיות מקורב הרבה פעמים גזיר. דוגמה של התנהגות זו ניתנת בהמשך, וזה קשור לעובדה כי בניגוד לפונקציות אנליטיות, ישנן פונקציות כלליות שערכיהן נקבעים לפי הנגזרת בנקודה בודדת.

טיילור זה משפט של asymptotic הטבע: זה רק אומר לנו שגיאה R_k ב. קירוב על ידי k-th סדר טיילור פולינום P_k נוטה לאפס מהר יותר מאשר כל nonzero k-th תואר פולינום כמו x → .. זה אינו אומר לנו מה גודל השגיאה בכל בטון השכונה של מרכז הרחבה, אבל לצורך זה יש מפורשת formulae עבור השארית טווח (כדלקמן), אשר תקפים תחת איזה נוספים סדירות הנחות על f. אלה גירסה משופרת של טיילור זה משפט בדרך כלל להוביל המדים הערכות על קירוב שגיאה בתוך שכונה קטנה של מרכז הרחבה, אבל ההערכות לא בהכרח להחזיק על שכונות שהן יותר מדי גדולות, אפילו אם הפונקציה f היא אנליטית. במצב כזה, אדם עשוי לבחור מספר פולינומי טיילור עם מרכזים שונים של התרחבות תהיה אמינה טיילור-קירובים של הפונקציה המקורית (ראה אנימציה בצד ימין.)

הוכחות

הוכחת משפר טיילור במשתנה יחיד ממשי

יהי${\displaystyle }$

לפי משפט טיילור,${\displaystyle }$

לכן מספיק להראות כי${\displaystyle }$

ההוכחה כאן מבוססת על יישום חוזר ונשנה של כלל לופיטל. נשים לב כי לכל j = 0,1,...,k−1, ${\displaystyle }$. לפיכך כל ה k−1 נגזרות ראשונות של המונה ב ${\displaystyle }$ נעלות כאשר ${\displaystyle }$ואותו דבר נכון לגבי המכנה. כמו כן, מכך שהפונקציה f גזירה k פעמים בכל נקודה, המונה שלה מכיל k-2 נגזרות בסביבת הנקודה a. ולכן, כל התנאים הנחוצים עבור משפט לופיטל מתקיימים, והשימוש בו מוצדק. אז,

${\begin{aligned}\lim _{x\to a}{\frac {f(x)-P(x)}{(x-a)^{k}}}&=\lim _{x\to a}{\frac {{\frac {d}{dx}}(f(x)-P(x))}{{\frac {d}{dx}}(x-a)^{k}}}=\cdots =\lim _{x\to a}{\frac {{\frac {d^{k-1}}{dx^{k-1}}}(f(x)-P(x))}{{\frac {d^{k-1}}{dx^{k-1}}}(x-a)^{k}}}\\&={\frac {1}{k!}}\lim _{x\to a}{\frac {f^{(k-1)}(x)-P^{(k-1)}(x)}{x-a}}\\&={\frac {1}{k!}}(f^{(k)}(a)-f^{(k)}(a))=0\end{aligned}}$

המעבר השני לפי האחרון השווין נובע מההגדרה של הנגזרת ב x = a.

ראה גם

• לורן סדרה
• Padé approximant
• ניוטון בסדרה

המלצות

• Apostol, Tom (1967), Calculus, Wiley, ISBN 0-471-00005-1
• Apostol, Tom (1974), Mathematical analysis, Addison–Wesley.
• Bartle, Robert G.; Sherbert, Donald R. (2011), Introduction to Real Analysis (4th ed.), Wiley, ISBN 978-0-471-43331-6
• Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer, ISBN 978-3-540-00662-6
• Kline, Morris (1972), Mathematical thought from ancient to modern times, Volume 2, Oxford University Press
• Kline, Morris (1998), Calculus: An Intuitive and Physical Approach, Dover, ISBN 0-486-40453-6
• Pedrick, George (1994), A First Course in Analysis, Springer, ISBN 0-387-94108-8
• Stromberg, Karl (1981), Introduction to classical real analysis, Wadsworth, ISBN 978-0-534-98012-2
• Rudin, Walter (1987), Real and complex analysis (3rd ed.), McGraw-Hill, ISBN 0-07-054234-1.