נקודת השוויון
נקודת שוויון היא מושג אסטרונומי שמשמעו הזמן בשנה שבו חצי כדור הארץ הדרומי והצפוני מוארים במידה שווה, ולפיכך אורך היום ואורך הלילה שווים. בצהרי היום לאורך קו המשווה בעת נקודת השוויון השמש נמצאת בזניט. גאומטרית, נקודת השוויון היא הזמן היחיד שבו יש זווית ישרה בין ציר הסיבוב של כדור הארץ לבין הקו הדמיוני המחבר את מרכז השמש עם מרכז כדור הארץ. נקודות השוויון מתרחשות בחודש מרץ ובחודש ספטמבר, בכל שנה.
ניתן להתייחס לנקודות השוויון גם כאל נקודות וירטואליות המונחות על מישור המילקה. מזלות האסטרולוגיה למשל, נמדדים בהתאם לנקודות שוויון אלו.
שוויון יום[עריכת קוד מקור | עריכה]
בעת מיקום השמש בנקודות השוויון, מספר שעות היום שווה למספר שעות הלילה. לצורך מדידת אורך יום, זריחת השמש מתרחשת כאשר מחצית מגוף השמש נצפה מעל לאופק המזרחי, ושקיעת החמה מתרחשת כאשר מחצית מגוף השמש נצפה יורד אל מתחת לאופק המערבי. בהתחשב בהגדרה זו, אורך היום (והלילה) הוא בדיוק 12 שעות בנקודת השוויון. עם זאת, שכיחה יותר הגדרת יום כמשך הזמן בו אור השמש מגיע אל האדמה בהיעדר מכשולים מקומיים. מאחר שהשמש אינה נקודה אלא עיגול, ואור השמש נשבר באטמוספירה ומשתקף בחזרה אל הארץ, היום בהגדרה זו יהיה ארוך יותר מהלילה בכמה דקות (כ-6 דקות בקו המשווה, ואף יותר מ-24 שעות בסמוך לקטבים), לכן השוויון הלכה למעשה מתרחש כמה ימים לפני נקודת השוויון האביבית וכמה ימים אחרי נקודת השוויון הסתווית.
בצהרי יום השוויון מצויה השמש בזווית ישרה מעל קו המשווה. ביום זה הזריחות והשקיעות מהירות מבשאר ימות השנה, ובקו המשווה כמעט שאין דמדומי בוקר או ערב.
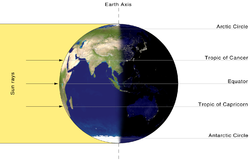
בין יום השוויון החל בחודש מרץ ליום השוויון החל בספטמבר, קווי הרוחב הצפוניים נוטים כלפי השמש עד לקו הרוחב 23.5° צפון הקרוי חוג הסרטן, הנקודה הצפונית ביותר שבה ניתן לצפות בשמש ישירות ממעל. הקו הדרומי המקביל נקרא חוג הגדי ומיקומו 23.5° דרום, ובו קווי הרוחב הדרומיים נוטים כלפי השמש בתקופה שבין ימי השוויון של ספטמבר ומרץ. האזור משני צדי קו-המשווה בין חוג הסרטן לחוג הגדי קרוי האזור הטרופי.
בחצי הכדור הצפוני, נקודת השוויון בחודש מרץ היא נקודת השוויון האביבית, ונקודת השוויון בחודש ספטמבר היא נקודת השוויון הסתווית. בחצי הכדור הדרומי המצב הפוך.
נקודת השוויון בחודש מרץ מתרחשת בדרך כלל בין היום ה-20 ליום ה-21 בחודש, ונקודת השוויון בחודש ספטמבר בין היום ה-22 ליום ה-23 בחודש. התאריכים משתנים משום שהשנה הטרופית אינה מורכבת ממספר ימים שלם, ומשום שמסלול כדור הארץ הוא אליפטי, לכן המועד בו מתרחשות נקודות השוויון אינו מחלק את השנה באופן שווה.
נדידה[עריכת קוד מקור | עריכה]
נדידתן האיטית של נקודות השוויון (Precession of the Equinoxes - "פרצסיה") קשורה ישירות לנקיפתו של ציר כדור הארץ סביב קוטבי מישור המילקה.
ציר כדור הארץ משלים מחזור נקיפה כל 25,800 שנים לערך. במשך זמן זה משתנים לאיטם מיקומי הכוכבים כפי שהם נמדדים במערכת הקואורדינטות השמימית המשוונית. שינוי הקואורדינטות נובע ישירות מנדידתה של מערכת הקואורדינטות עצמה. שינוי הקואורדינטות של נקודות השוויון הוא בקצב של כמעלה אחת מדי 72 שנים (בכיוון השעון במבט מלמעלה, כלומר מעל קוטבו הצפוני של כדור הארץ).
בתרבות המערבית, היה זה האסטרונום היפרכוס שגילה בשנת 130 לפנה"ס, את נדידת נקודות השוויון. כיום משערים כי תרבויות עתיקות יותר (כגון מצרים העתיקה ובבל) הקדימו אותו.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- למה היום ארוך מהלילה?
- ימי השוויון וימי ההיפוך – העובדות אל מול התכונות המיוחסות להם
- מדוע למרות שטכנית זה נכון, אין באמת שוויון בין היום והלילה הידען
- בר חיון, יום השוויון האביבי: היום הראשון של האביב, באתר סוכנות החלל הישראלית, 20 במרץ 2017
- יהונתן ברקהיים, הגלובוס בן שנות אלפיים, במדור "מדע במבט-על" באתר של מכון דוידסון לחינוך מדעי, 22 בספטמבר 2023
- נקודת השוויון, באתר אנציקלופדיה בריטניקה (באנגלית)
