מערכת הקואורדינטות המשוונית
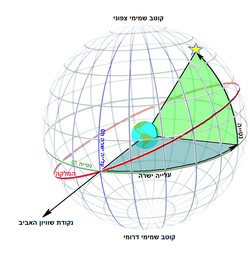
מערכת הקואורדינטות המשוונית היא מערכת הקואורדינטות השמימית הנפוצה ביותר לשימוש באסטרונומיה.
המערכת משמשת לתיאור מיקום גופים על כיפת השמים הכדורית כפי שתיראה לצופה היפותטי שיעמוד במרכז כדור הארץ, במקומו (כלומר, כדור הארץ לא יסתיר לו את השמים). זאת בניגוד למערכת הקואורדינטות ההוריזונטאלית שמתארת את מיקום הגופים על כיפת השמים שנראית לצופה אנושי מסוים הממוקם על קרום כדור הארץ. כדי שהמערכת תתאר את מיקומם הממשי של גופים בחלל, נהוג להוסיף פרמטר שיציין את המרחק שלהם מכדור הארץ.
במערכת זו מצוינים על כיפת השמים קווי אורך ורוחב המקבילים לקווי האורך והרוחב של כדור הארץ. במונחים של מערכות קואורדינטות שמימיות ניתן שקו המשווה של המערכת הוא קו המשווה השמימי שנוצר מהיטלו של קו המשווה של כדור הארץ על כיפת השמים. קו האורך 0 של המערכת מונח על נקודת שוויון האביב ומזרחית לו ערכי קווי האורך מקבלים ערכים חיוביים.
בגלל נקיפת ציר כדור הארץ מתרחשת נדידת נקודת שוויון האביב, דבר שגורם לשינוי מתמיד בערכים הניתנים במערכת זו. לכן יש לציין יחד עם נתוני המיקום גם את הזמן בו הם נמדדו. זמן זה נקרא "תקופת היחוס".
הקואורדינטות[עריכת קוד מקור | עריכה]
הקואורדינטות של מערכת זו הן קואורדינטות כדוריות, שמרכזן בכדור הארץ.
אם נסמן, - וקטור העתק במערכת הקואורדנטית המשוונית, אז ערכי הקואורדינטות של יהיו:
- - עלייה ישרה (right ascension) - הזווית בין נקודת השוויון האביבית של כדור הארץ לבין היטל על מישור המשווה של כדור הארץ, כאשר מישור המשווה הוא המישור העובר דרך קו המשווה של כדור הארץ. (מקביל לערך קו האורך)
- - נטייה או דקלינציה (declination) - הזווית בין ההיטל של על מישור המשווה לבין עצמו. (מקביל לערך קו הרוחב)
- r - גודלו של .
- t - קואורדינטת הזמן.
יחידות מקובלות[עריכת קוד מקור | עריכה]
היחידות בהן מקובל להשתמש כאשר מציינים מיקום במערכת הקואורדינטות המשוונית הן:
- היחידות של - מעלות (דקות ושניות), ואז ערכה של הוא בין 90- ל-90+ מעלות.
- היחידות של - מגדירים את היחידות הבאות: 15 מעלות=1 שעה, 1 שעה=60 דקות, 1 דקה=60 שניות. שעה דקה ושנייה במקרה הזה הן יחידות חסרות גודל של הזווית ומישור המשווה מחולק על ידי יחידות אלה ל-24 שעות, כלומר ערכו של הוא בין 0 ל-24 שעות.
- היחידות המקובלות לשימוש של קואורדינטה r הן יחידות האורך שנת אור, או פארסק.
- t - בדרך כלל מקובל לציין רק את תקופת הייחוס (epoch) של המערכת, כאשר תקופות היחוס המקובלות הן B1950 − 31 בדצמבר 1949, 22:09 (שעון גריניץ') או J2000 − 1 בינואר 2000, 12:00 (זמן אוניברסלי מתואם).
השפעות נקיפת ציר כדור הארץ[עריכת קוד מקור | עריכה]
כיוון ציר הסיבוב של כדור הארץ משתנה ביחס למישור המילקה עם הזמן וכתוצאה מכך גם הטרנספורמציה בין מערכת הקואורדינטות המשוונית למערכת הקואורדינטות האקליפטית תלויה בזמן. השינוי הדומיננטי ביותר של כיוון ציר הסיבוב של כדור הארץ ביחס למישור המילקה נובע מהתנועה האליפטית של כיוון ציר הסיבוב של כדור הארץ ביחס לכיוון מישור המילקה. תנועה זו נקראת הפרצסיה (נקיפה) הירחית-שמשית של כדור הארץ והיא מוסיפה לטרנספורמציה רכיב תלוי זמן בעל מחזור של 26,000 שנה בקירוב. ישנן גם השפעות אחרות על הטרנספורמציה כמו הנוטציה של ציר סיבוב כדור הארץ והשפעות אחרות שאינן מחזוריות כגון השפעת כוכבי הלכת האחרים במערכת השמש על כדור הארץ. אם רוצים לקחת בחשבון את כל ההשפעות האלו, אז לא ניתן לחשב בצורה אנליטית את השינויים הצפויים בעתיד (או בעבר) של תנועת ציר סיבוב הארץ. לכן יש לפעמים צורך להשתמש במדידות או בהערכות המבוססות על שיטות חישוב נומריות על מנת לבצע טרנספורמציה בין מערכת הקואורדינטות המשוונית למערכת הקואורדינטות האקליפטית בדיוק גבוה מספיק.
המרת נתונים מהמערכת האקליפטית למשוונית[עריכת קוד מקור | עריכה]
- יהיו λ ו-β קווי האורך והרוחב (בהתאמה) האקליפטיים.
- יהיו α ו-δ הנטייה והעלייה הישרה (בהתאמה).
- יהיה ε זווית הנטייה של ציר כדור הארץ, שהיא 23.439281°
מאקליפטי למשווני[עריכת קוד מקור | עריכה]
sin δ = sin ε sin λ cos β + cos ε sin β
cos α cos δ = cos λ cos β
sin α cos δ = cos ε sin λ cos β - sin ε sin β
ממשווני לאקליפטי[עריכת קוד מקור | עריכה]
sin β = cos ε sin δ - sin α cos δ sin ε
cos λ cos β = cos α cos δ
sin λ cos β = sin ε sin δ + sin α cos δ cos ε
הערה לגבי פתירת מערכות המשוואות[עריכת קוד מקור | עריכה]
על אף שנראה מתבקש "לפשט" את מערכות המשוואות ולהישאר עם ביטוי אחד לכל רכיב, אין הדבר כדאי שכן הפונקציות הטריגונומטריות אינן חד-חד ערכיות. לדוגמה, במערכת השנייה ניתן לחלק את שתי המשוואות האחרונות זו בזו ולקבל ביטוי יחיד ל-tan λ (), אולם צעד זה לא יהיה כדאי מאחר שפונקציית tan-1 "מניחה" שהזווית המבוקשת היא בין 0-180° בעוד ש-λ יכולה לקבל כל ערך בין 0-360°. כאשר מדובר ב-β הדבר לא משמעותי מאחר הערך שלה מוגבל מראש ל-90°- עד 90°+.
בפועל, כאשר מדובר בעצמים הקרובים למישור המלקה, מספיקה משוואה אחת כדי לקבוע את λ, משום שהיא באותו רביע כמו α.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- הערך "קורדינאטות שמימיות", באתר אסטרופדיה




