שכיח
בסטטיסטיקה, השכיח הוא הערך בעל השכיחות הגבוהה ביותר בקבוצת נתונים. במילים אחרות, זהו הערך שהופיע במדגם יותר פעמים מכל ערך אחר.
כמו הממוצע והחציון, השכיח משמש כאמצעי להבעת מידע חשוב על משתנה מקרי או אוכלוסייה באמצעות מספר בודד. יתרונו המשמעותי של השכיח על שאר מדדי המרכז, כמו הממוצע והחציון, הוא שהוא מוגדר גם למשתנה בעל ערכים שמיים.
אם כמה ערכים הם בעלי השכיחות הגבוהה ביותר במדגם, כל אחד מהם נחשב לשכיח. המקרה הקיצוני ביותר מתרחש בהתפלגויות אחידות, שבהן כל הערכים שכיחים באותה מידה. בהתפלגויות סימטריות יונימודליות ("חד-דבשתיות"), כמו ההתפלגות הנורמלית, החציון, השכיח והממוצע מתלכדים.
חישוב השכיח
[עריכת קוד מקור | עריכה]במדגם בדיד
[עריכת קוד מקור | עריכה]השכיח של מדגם הוא הערך המופיע בו בכמות הגבוהה ביותר. לדוגמה, השכיח של המדגם [1, 3, 6, 6, 6, 6, 7, 7, 12, 12, 17] הוא 6. לעומת זאת, ברשימת הנתונים [1, 1, 2, 4, 4] השכיח אינו ייחודי - קיימים שני ערכים בעלי אותה שכיחות, שהיא הגבוהה ביותר במדגם. ניתן לומר שההתפלגות היא דו-שיאית (דו-דבשתית), בעוד שקבוצה עם יותר משני שכיחים יכולה להיות מתוארת כרב-שיאית (רב-דבשתית).
במדגם רציף
[עריכת קוד מקור | עריכה]כאשר המדגם הוא התפלגות רציפה, כגון [... .935, 1.211 ..., 2.430 ..., 3.668 ..., 3.874 ...], המושג הוא בלתי שימושי בצורתו הגולמית, שכן אין בו שני ערכים זהים, ולכן כל ערך יופיע בדיוק פעם אחת. על מנת להעריך את השכיח, מקובל לסדר את הנתונים במחלקות שוות רוחב, כמו להכנת היסטוגרמה, ולחשב את שכיחותה של כל מחלקה. ניתן למצוא בקלות את המחלקה השכיחה - המחלקה שבה ההיסטוגרמה מגיעה לשיא - ואמצע מחלקה זו הוא השכיח. החיסרון בכך הוא שבדגימות קטנות או בינוניות, עלולה להיווצר הטיה בהתאם לרוחב המחלקה. דרך אחרת לחישוב השכיח במדגם רציף היא למצוא את נקודת המקסימום של פונקציית צפיפות ההסתברות אשר נאמדת בעזרת החלקה עם פונקציית גרעין (kernel density estimation).
הצגה גרפית
[עריכת קוד מקור | עריכה]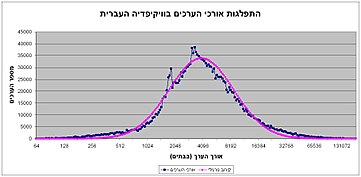
בסדרת ערכים, השכיח מוגדר כאמור על ידי ספירת ההופעות של הערכים השונים וניתן להציג את הרשימה כולה, אך דרך זו אינה נוחה. קיימות מספר דרכים להצגה גרפית של השכיח: ניתן לסדר את הערכים בטבלת שכיחויות- בה ליד כל ערך יופיע מספר הפעמים שבו נדגם. טבלה כזו יכולה לשמש לבניית דיאגרמת מקלות או גרף שבו מיקום נקודה מציין את הערך ושכיחותו. בהצגות כאלו, ניתן לאתר את השכיח בקלות: הערך השכיח הוא זה שהעמודה או הנקודה המייצגת אותו היא הגבוהה ביותר - בעל הצפיפות הגבוהה ביותר. כאשר מספר הערכים גדול ניתן לחלק את הערכים למחלקות ולהציג את שכיחותן בהיסטוגרמה. בצורת הצגה כזאת, השכיח הוא אמצע המחלקה השכיחה ביותר. במדגם רציף, שבו ניתן להציג את ההתפלגות בקו אחד, ניתן לאתר את השכיח בגרף על ידי מציאת נקודת המקסימום שלו.
השוואה למדדי מרכז אחרים
[עריכת קוד מקור | עריכה]
הטבלה הבאה מדגימה ששלושת מדדי המיקום המרכזיים אינם חייבים להסכים זה עם זה:
| סוג | תיאור | דוגמה | תוצאה |
|---|---|---|---|
| ממוצע חשבוני | סכום ערכי המדגם מחולק במספרם | 7/(1+2+2+3+4+7+9) | 4 |
| חציון | הערך האמצעי בסידור עולה של הערכים | 1,2,2,3,4,7,9 | 3 |
| שכיח | הערך הנפוץ ביותר במדגם | 1,2,2,3,4,7,9 | 2 |
בניגוד לממוצע ולחציון, המושג "שכיח" הגיוני וישים גם על ערכים שמיים. למשל, אם המדגם הוא של שמות משפחה בישראל, והשם "כהן" מופיע הכי הרבה פעמים, השכיח יהיה "כהן". מובן שבדגימה כזו לא ניתן לחשב ממוצע או חציון. במערכת בחירות שבה המנצח נקבע על פי הרוב, המנצח הוא השכיח. שני שכיחים ומעלה ידרשו תהליך שובר שוויון. בניגוד לחציון, שהגיוני להשתמש בו רק כאשר יש סדר ליניארי בין הערכים האפשריים, השכיח אינו דורש זאת- בכל מדגם יש משמעות למושג זה.
פונקציית ההפסד
[עריכת קוד מקור | עריכה]השכיח של מדגם מוגדר כערך שמספר הערכים השונים ממנו הוא הקטן ביותר. במילים אחרות, השכיח הוא הממזער של פונקציית ההפסד הבאה:
כאשר .
פונקציית ההפסד בעצם מתארת בכתיב מתמטי את המקרה הבא: בכל פעם בוחרים ערך אקראי מהרשימה. המטרה היא לנחש אותו, כאשר "ניצחון" הוא ניחוש נכון של הערך ו"הפסד" הוא כל ניחוש שאינו נכון. אנו מעוניינים "לנצח" כמה שיותר פעמים באמצעות שימוש באותו המספר. באיזה מספר עדיף לבחור? בשכיח כמובן. זהו הערך שאיתו נצא עם מספר ה"הפסדים" הקטן ביותר.



