עמוד טיילור

משפט טיילור-פראודמן מבטיח כי תנועת הזורם אחידה לאורך עמודה המוגדרת על ידי הכדור השקוע. בגלל תנאי השפה בתקרת המיכל, המהירות האנכית של פרודות הזורם חייבת להתאפס שם, ולפיכך המהירות האנכית של הזורם חייבת להתאפס לאורך כל העמודה. כתוצאה, התנועה של הזורם מעל ומתחת לעצם הנע נאלצת לבצע סירקולציה אופקית לחלוטין.

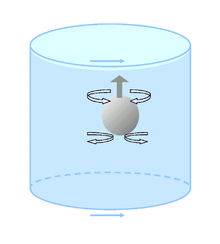
עמוד טיילור (באנגלית: Taylor column) הוא תופעה במכניקת הזורמים המתרחשת כתוצאה מאפקט קוריוליס. במסגרת התופעה, זורמים המסתחררים במהירות זוויתית גבוהה וסופגים הפרעה קלה בשדה המהירויות שלהם כפי שאלו נצפות ממערכת ייחוס המסתובבת ביחד עם הזורם, נוטים להסתדר בעמודים המקבילים לציר הסיבוב אשר מהירות הזורם לא משתנה לאורכם. עמודים אלה נקראים "עמודי טיילור", על שם ג'פרי אינגרם טיילור, מחשובי חוקרי מכניקת הזורמים במאה ה-20.

ההוכחה המתמטית לקביעה הזו מבוססת על פישוט משוואות נאוויה-סטוקס במערכת ייחוס מסתובבת באמצעות התייחסות להתנהגות הזורם במצב עמיד ובגבול של מספר ריינולדס, מספר רוסבי ומספר אקמן נמוכים. בגבול הזה, משפט טיילור-פראודמן מראה כי הנגזרת הכיוונית של שדה המהירויות של הזורם מתאפסת בכיוון ציר הסיבוב. כתוצאה מכך, רכיב מהירות הזורם בכיוון ציר הסיבוב חייב להתאפס כאשר הזורם מצוי במיכל סגור המגביל את תנועתו, מה שמבטיח כי תנועת הזורם היא דו-ממדית.

לעובדה הזאת יש השלכות מרחיקות לכת על השפעת זורמים על גופים הנתונים בתוכם. עצם הנע במקביל לציר הסיבוב של זורם מסתובב יחווה יותר כוח גרר לעומת כאשר היה נע בזורם לא מסתובב. לדוגמה, כדור בעל ציפה חזקה למדי (כמו למשל כדור פינג-פונג) המוצב בקרקעית מיכל מים מסתובב, יעלה אל פני השטח לאט יותר מאשר בזורם לא מסתובב. ניתן להסביר זאת בצורה מעט פשטנית על ידי כך שאודות לכוח קוריוליס, אלמנטי זורם הנקרים בדרכו של הכדור ונדחפים החוצה ממסלולו נוטים לבצע סירקולציה חזרה לנקודה ממנה הם הוסטו. בזורם לא מסתובב חלקי הזורם נפרדים בחזית הכדור הנוסק, נעים מסביבו (קווי הזרם מראים תנועה אנכית של פרודות הזורם), ונפגשים חזרה בחלק האחורי שלו, תוך שהם מפעילים מעט גרר על הכדור. בזורם מסתובב, לעומת זאת, נטייתם הטבעית של אלמנטי הזורם לחזור לנקודת ההתחלה גורמת להיערמות לחץ סטטי גבוה בחזית הכדור, בעוד שהסירקוציה ההפוכה בחלקו האחורי גורמת לנפילת הלחץ הסטטי. ככל שתדירות סיבוב המיכל גבוהה יותר, כך קטן יותר רדיוס המעגל האינרציאלי שמתווה חתיכת הזורם, וגדול יותר הפרש הלחצים בין חזית הכדור וצדו האחורי.

עובדת קיומם של "עמודי טיילור" ריתקה את בני זמנו של טיילור, בין היתר משום שהיא מתארת סוג של "פעולה מרחוק" הקיימת בזורמים מסתובבים - במהירות סיבוב גבוהה מאוד, הזורם מציג דרגה מסוימת של קשיחות; כלומר, פרודות הזורם המרכיבות עמודה נתונה מסונכרנות ומתנהגות כגוף אחד.

מעגל אינרציאלי שמתווה אלמנט זורם (הנקודה השחורה).

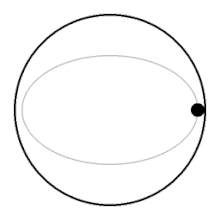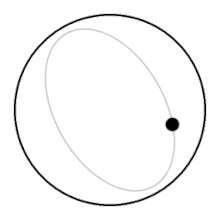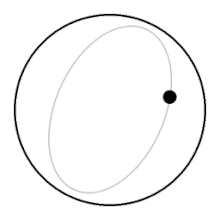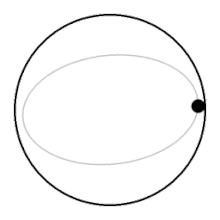
היסטוריה

עמודי טיילור נצפו לראשונה על ידי לורד קלווין ב-1868. תצפיותיו מתועדות במכתב ששלח אליו אחיו של קלווין, ג'יימס תומסון:

"אני פגשתי את פרופ' טייט בבלפסט בשבוע שעבר והוא ציין בפניי ניסוי אשר ערכת, במסגרתו הצבת חתיכת שעם על הציר של מערבולת מים בעלת מהירות זוויתית אחידה בכל חלקיה, וקיבלת את התוצאה שחתיכת השעם נותרה במפלס קבוע מבלי לצוף מעלה; והוא ציין גם שכאשר הצבת שתי חתיכות כאלה במפלסים שונים על ציר הסיבוב, שניהם נשארו איפה שהצבת אותם, ושאם דחפת את העליון מעט מטה אז גם התחתון זז מעט מטה, ממש כאילו הייתה מסה קשיחה של מים ביניהם."

התופעה מוסברת דרך משפט טיילור-פראודמן והיא נחקרה על ידי טיילור וחוקרים נוספים. טיילור ערך סדרת הדגמות ניסוייות מרהיבות לתופעה: הוא הדגים אותה בעזרת כדור שנע לאורך ציר הסיבוב, והראה שגליל הנע בניצב לציר הסיבוב האנכי במערכת הייחוס של הזורם גורר איתו מערבולת גלילית אנכית הנמתחת לאורך כל הזורם. כמו כן חקר באופן מעמיק ומתמטי יותר את התופעה מקודמיו. כהוקרה לתרומותיו אלו, עמוד הערבוליות הגלילי שנוצר מעל עצם המתקדם בתוך זורם מסתובב נקרא "עמוד טיילור".

המנגנון הפיזיקלי מאחורי הגדלת הגרר

אודות לתנועת הכדור במהירות קבועה בכיוון ציר הסיבוב, מתפתחת בחזית הכדור סירקולציה במגמה הפוכה למגמת סיבוב מיכל הזורם, בעוד שמאחורי הכדור מתפתחת סירקולציה במגמה זהה לסיבוב המיכל. ההסבר לכך לא יכול לנבוע מפרק הזמן בו הכדור נע במהירות קבועה, אלא מפרק הזמן שקדם לו, במהלכו הכדור האיץ עד שהגיע למהירות הטרמינלית שלו. בפרק הזמן הזה הנחת עמידות הזרימה של משפט טיילור-פראודמן אינה תקפה, וישנה גם תנועה אנכית של הזורם מסביב לכדור. מכיוון שהזרימה מסביב לכדור אינה דחיסה, הדיברגנץ של שדה המהירויות חייב להתאפס בכל נקודה. לכן, מהירות אנכית של פרודות הזורם המשתנה לאורך ישר המקביל לציר הסיבוב האנכי ($\partial u_{z}/\partial z\neq 0$) גוררת התכנסות או התבדרות של קווי הזרם במישור האופקי. אפקט קוריוליס גורם לזרימה שבנקודות התבדרות של הזרימה במישור האופקי (שניתן להסתכל עליהן כעל "מקור" של שדה הזרימה) לפתח ערבוליות במגמה הפוכה לסיבוב הזורם, ולזרימה בנקודות התכנסות לפתח ערבוליות במגמה זהה לסיבוב המיכל, בדומה לזרימה הציקלונית או האנטי-ציקלונית המתפתחת מסביב לשקע ברומטרי ורמה ברומטרית, בהתאמה.

מכיוון שפרודות הזורם הנקרות בדרכו של הכדור בשלב ההאצה נפרדות בחזית שלו ונפגשות שוב בחלקו האחורי, ניתן להסיק שבשלב ההאצה חזית הכדור משמשת כמקור דו-ממדי בעוד שחלקו האחורי משמש כבור דו-ממדי. כתוצאה, עם הגעתו של הכדור למהירות הטרמינלית שלו, ערבוליות הזרימה מסביב לכדור מתייצבת באופן שתואר מקודם. כוח קוריוליס פועל רדיאלית החוצה עבור תנועת סיבוב המתואמת עם סיבוב מערכת הייחוס כולה, ופנימה עבור תנועת סיבוב המנוגדת לסיבוב מערכת הייחוס כולה. לכן, הלחץ הסטטי במרכז מעגל אינרציאלי בכל אחד מהמקרים צריך להיות קטן או גדול בהתאמה, מהלחץ על שפת המעגל הזה. כלומר, משהתעצבה התפלגות הערבוליות והלחץ הסטטי מסביב לכדור, הלחץ הסטטי בחזית חייב לגדול משמעותית בעוד שהלחץ בחלק האחורי חייב לפחות משמעותית. מידת ההגדלה של הלחץ בחזית נמצאת ביחס ישר למהירות הזוויתית של סיבוב המיכל, $\Omega$.

תיאור התופעה באמצעות גלים אינרציאליים

גלים אינרציאליים הם ההתגלמות של פרטורבציות במהירויות הזורם המתקדמות בתוכו באמצעות אפקט קוריוליס. הגלים הללו ניחנים בתכונות הייחודיות הבאות:

• מהירות החבורה שלהם ניצבת למהירות המופע שלהם (כלומר ${\vec {C_{g}}}\cdot {\vec {C_{p}}}=0$).
• תדירות הגל $\omega$ תלויה אך רק בכיוון וקטור הגל שלו ${\vec {k}}$; היא מרבית כאשר וקטור הגל מצביע באותו כיוון כמו ציר הסיבוב (אז ערכה הוא $2\Omega$), ומתאפסת כאשר הוא נח במישור הניצב לציר הסיבוב. במסגרת התאוריה של גלים אינרציאליים, ניתן להראות גם שמהירות החבורה, שהיא גם המהירות האמיתית של העברת האנרגיה, גדלה ככל שתדירות הגל $\omega$ קטנה.

אחת מהנחות היסוד של המודל של עמוד טיילור היא שהעצם המשוקע נע לאט מספיק כך שמספר רוסבי יהיה קטן מספיק. נקודת המבט של גלים אינרציאליים מספקת לפיכך זווית הסתכלות נוספת על התופעה: עצמים הנעים בתוך זורם מסתובב מייצרים גלים אינרציאליים בתדירות אופיינית שהיא מסדר גודל של מהירות התנועה שלהם U חלקי האורך האופייני שלהם d (למשל רדיוס הכדור במקרה של עצם כדורי). אילו התדירות הזאת מקיימת:

$f\propto U/d<<\Omega$

אז ניתן לומר שהעצם יוצר גלים אינרציאליים בתדירות נמוכה. משמעות הדבר היא שוקטור הגל "כמעט" ונח במישור הניצב לציר הסיבוב, ומהירות החבורה תהיה גדולה מאוד ותכוון לאורך ציר הסיבוב. כתוצאה, מופע הגלים האינרציאליים כמעט שלא ישתנה בכיוון ציר הסיבוב, מה שאומר שמהירות הזורם תהיה אחידה לאורך עמודות המקבילות לציר הסיבוב (ואלו הם "עמודי טיילור"). כמו כן, מהירות החבורה של הגלים מאפשרת לחלק את הזורם לאזור ש"יודע" על הימצאות הגוף הנע ואזור ש"לא יודע" עליו; גובה עמוד טיילור שמעל העצם יקיים: $l\propto C_{g}t$.