צידוד (סטטיסטיקה)
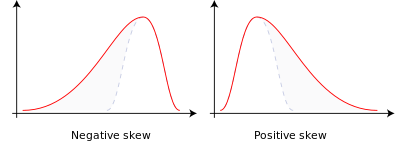
בסטטיסטיקה, צידוד (באנגלית: Skewness) הוא מדד מקובל לחוסר הסימטריה של פונקציית צפיפות או התפלגות של משתנה מקרי ממשי. למשתנה בעל צידוד חיובי יש נטייה לקבל ערכים גבוהים ורחוקים מן הממוצע, יותר מאשר ערכים נמוכים הרחוקים ממנו, ובגרף של פונקציית הצפיפות ניכר שהזנב הימני ארוך ועבה יותר מן השמאלי. כאשר הצידוד שלילי, הצדדים מתהפכים. בפונקציה סימטרית ביחס לתוחלת, הצידוד הוא אפס.
הצידוד של משתנה X, המסומן ב- מוגדר מתוך המומנט השלישי לפי הנוסחה , כאשר הוא המומנט השלישי הממורכז סביב התוחלת , ו- היא סטיית התקן של X.
אחרי הפרמטרים החשובים ביותר של פונקציית התפלגות, התוחלת והשונות, המבוססים על המומנט הראשון והשני, ולצד הצידוד, נמצאת בשימוש הגבנוניות, המבוססת על המומנט הרביעי.
צידוד של מדגם[עריכת קוד מקור | עריכה]
צידוד מוגדר לא רק עבור התפלגות תאורטית, אלא גם עבור מדגם סופי. הצידוד של מדגם מחושב לפי הנוסחה , כאשר הוא הממוצע, הוא המומנט השלישי הממורכז של המדגם, ו- היא שונות המדגם.
כאשר מבקשים לאמוד את הצידוד של ההתפלגות מתוך הצידוד של מדגם, הוא מהווה אומד מוטה. מקובל לתקן אותו לפי הנוסחה , שבה הוא אומד חסר הטיה למומנט המרכזי השלישי ו- אומד חסר הטיה למומנט המרכזי השני, אלא שאפילו תיקון זה אינו מספק אומד חסר הטיה, ובמקרים מסוימים התוחלת שלו הפוכה בסימנה מן הצידוד האמיתי.
צידוד של משתנים קרובים[עריכת קוד מקור | עריכה]
- הצידוד אינו מושפע מהזזה: .
- הצידוד אדיש לכפל בקבוע ותלוי רק בסימן.
- אם 0<a קבוע חיובי: .
- אם 0>a קבוע שלילי:.
- הצידוד של סכום משתנים מקריים בלתי תלויים עם אותם מומנטים שני ושלישי הוא:
; בפרט, הצידוד של ממוצע משתנים בלתי תלויים הולך וקטן כאשר המדגם גדל.
שימושים[עריכת קוד מקור | עריכה]
ביישומים סטטיסטיים מקובל להניח במקרים רבים שההתפלגות בה עוסקים היא התפלגות נורמלית, שהיא התפלגות סימטרית. המציאות אינה תמיד סימטרית, וזוהי סטייה שחשוב לכמת כדי להעריך עד כמה הנחת הנורמליות פגומה. הצידוד מאפשר להסיק לאיזה כיוון יהיו רוב הסטיות הגדולות מן הממוצע.
דוגמאות[עריכת קוד מקור | עריכה]
צידוד חיובי: המשכורות במשק מתאפיינות בכך שהסטייה מהמשכורת השכיחה כלפי מטה מוגבלת, מכיוון שלא ניתן לקבל משכורת שלילית ובנוסף קיים חוק שכר מינימום, ומנגד - משכורות של קבוצה קטנה חורגות בצורה קיצונית כלפי מעלה. כתוצאה מכך, השכר החציוני נמוך מהשכר הממוצע.
כך גם לגבי מדידת זמנים, למשל בביצוע מטלות: לא ניתן לחרוג מתחת לזמן השכיח בהרבה, כי זמן הביצוע אינו יכול להיות 0. לעומת זאת, תפקוד לקוי או חוסר מיומנות יובילו לזמנים ארוכים בהרבה מהשכיח.
צידוד שלילי: החציון בציונים במבחן צפוי להיות בסביבות 70–80. לא ניתן לחרוג הרבה מעבר לכך כי הציון המקסימלי הוא 100, אך ניתן לחרוג כלפי מטה במידה רבה ולקבל 0. כתוצאה מכך נצפה שהממוצע בבחינה יהיה נמוך מהשכיח ומהחציון.
חלופות[עריכת קוד מקור | עריכה]
הסטטיסטיקאי הנודע קרל פירסון הציע שני מדדים אחרים למדידת חוסר הסימטריה של התפלגות או מדגם:
מדדים אלו שימושיים בעיקר במדגמים גדולים, ולא כאשר עוסקים בהתפלגויות תאורטיות. בנוסף, אין ערובה לכך שהם יהיו בעלי אותו סימן כמו הצידוד.






















