גרף של פונקציה

בערך זה |
גרף של פונקציה הוא אוסף כל הזוגות הסדורים של משתנה מסוים עם ערך הפונקציה המתאים לו, כלומר גרף הפונקציה אמור להתבסס על פי שתי אותיות [X+Y] המסמנות את הגרף עצמו. בתרגיל מסוים של משוואות ה - x תקדים את ה - y. עבור פונקציה מסוימת. לרוב הכוונה היא לציור של אוסף זה בתור נקודות במישור לפי מערכת צירים קרטזית, אולם צורת הצגה זו אפשרית רק עבור פונקציות ממשיות במשתנה יחיד; עם זאת, מושג הגרף קיים גם עבור פונקציות במספר משתנים.
במערכת צירים דו־ממדית את ציר איברי תחום הפונקציה לרוב נהוג לסמן כ- ואת ציר איברי הטווח נהוג לסמן כ-. בנקודה (זוג סדור) בגרף במערכת צירים דו־ממדית, האיבר הראשון (שיעור X של הנקודה) בזוג נקרא גם אבסציסה (Abscissa) והשני (שיעור Y) נקרא גם אורדינטה (Ordinate).
הגדרה פורמלית[עריכת קוד מקור | עריכה]
בהינתן פונקציה שתחומה , גרף הפונקציה היא הקבוצה של הזוגות הסדורים .
נשים לב כי עבור פונקציה ממשית ב- משתנים, גרף הפונקציה הוא תת-קבוצה של המרחב האוקלידי . המקרה הפרטי המוכר הוא זה של פונקציה במשתנה יחיד, אז הגרף הוא תת-קבוצה של המישור - .
דוגמאות[עריכת קוד מקור | עריכה]
- ישר - גרף שמייצג פולינום ממעלה ראשונה () שיפועו, כלומר טנגנס הזווית שלו עם ציר ה-, הוא והוא חותך את ציר ה- בנקודה .
- פרבולה - מייצגת פולינום ממעלה שנייה. נראית כמעין קשת מתרחבת ( כאשר a אינו אפס) אם חיובי הפרבולה פתוחה כלפי מעלה (כלומר קמורה) ואם הוא שלילי, אז היא פתוחה כלפי מטה (קעורה).
- היפרבולה - מייצגת פונקציה מהסוג
נקודות מיוחדות על גרפים של פונקציות ממשיות:
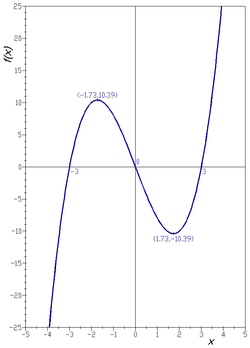
- מינימום ומקסימום - הנקודות הגבוהות והנמוכות ביותר בסביבה כלשהי של הנקודה, כלומר ערכי ה- הגדולים והקטנים ביותר יחסית לסביבתם בהתאמה. אם הפונקציה גזירה בנקודות אלו - הנגזרת תתאפס.
- נקודת פיתול - נקודת מעבר מקמירות לקעירות.
- נקודות אפס -
- כאשר הגרף חותך את ציר ה-X. כדי למצוא אותו משווים את הפונקציה ל-0.
- כאשר הגרף חותך את ציר ה-Y. כדי למצוא אותו מציבים בפונקציה X=0.
- נקודת שאיפה- נקודה ב-X שלא מוגדר לה Y ולכן הפונקציה שואפת אליה משני צדדיה (כגון אסימפטוטות בהיפרבולה), או נקודה ב-Y שהפונקציה לא תגיע אליה מעולם אבל שואפת אליה.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- יישום ג'אווה שמאפשר לשרטט גרפים של פונקציות
- מציאת נקודות על גרפים, באתר לרגו (LerGO)
- גרף של פונקציה, באתר MathWorld (באנגלית)

















