תורת התנודות
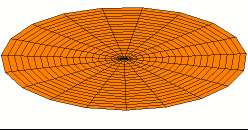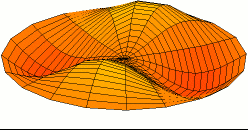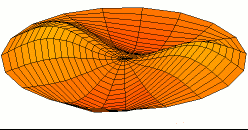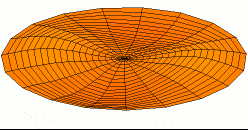
בפיזיקה ובניתוח מערכות, תנודה היא שינוי במצב של מערכת לאורך זמן. בדרך כלל המונח מתאר שינוי מחזורי בקירוב. המונחים "ויברציה", "רעידה" או "רטט" משמשים כדי לתאר תנודה מכנית ולעיתים אף משמשים כשם נרדף לתנודה. תנודה מתרחשת לא רק במערכות פיזיקליות אלא גם במערכות ביולוגיות ובמערכות חברתיות.
הגורמים הבסיסיים לניתוח תנודות הם תגובת המערכת (אלסטיות למשל), כוח מאלץ (מתחיל ומקיים את התנודה) וריסון (משכך את התנודה).
ניתן לראות דוגמאות לתנודות בתחומים רבים מאוד. החל מתנודות הגלים בים ועד לתנודות מיתרי הגיטרה. תנודות אלה הן תנודות מרוסנות - כלומר דועכות עם הזמן, ומעבירות את האנרגיה שלהם לאנרגיה תרמית, כלומר לחום. משוואת הגלים היא אחת המשוואות הפשוטות המתארות התקדמות של תנודה במרחב.
אחת התופעות המוכרות בתורת התנודות היא התהודה, שבה מופעל כוח בתדירות השווה לתדירות הטבעית של המערכת. ללא ריסון כלשהו (חיכוך למשל), המערכת מתנודדת יותר ויותר חזק עד להתמוטטות.
במכניקה הקלאסית[עריכת קוד מקור | עריכה]
תנודות חופשיות - ריסון ויסקוזי[עריכת קוד מקור | עריכה]
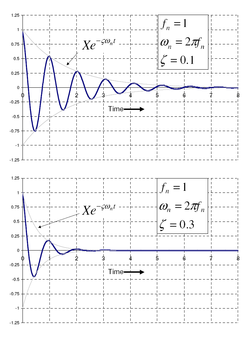
במערכת בעלת דרגת חופש אחת[1], כאשר הכוח F שווה לאפס, ניתן לתאר את משוואת התנועה של המערכת בצד שמאל כך: .
בתורת התנודות נהוג להגדיר שלושה ערכים המבטאים את השפעת התנודה על המערכת:
1. התדירות הטבעית של המערכת המתוארת על ידי ושווה ל-.
2. ריסון קריטי המתואר על ידי ושווה ל-.
3. יחס הריסון המתואר על ידי ושווה ליחס בין ל-.
למשוואת התנועה, אם כן, ישנם שלושה פתרונות המבטאים התנהגות שונה של המערכת מבחינת תנודות:
1 ו- 2. כאשר - ריסון על קריטי וקריטי. פתרונות משוואת התנועה הם:
כאשר (ריסון על קריטי)
כאשר (ריסון קריטי)
3. כאשר - ריסון תת-קריטי - כלומר יש תנודות.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- תורת התנודות, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ במערכת בעלת מספר דרגות חופש, משוואת התנועה זהה, אך מיוצגת על ידי הפרמטרים כמטריצות: M - מטריצת המסה, K - מטריצת הקשיחות ו-C - מטריצת הריסון, כך שהמשוואה היא אוסף של מטריצות כפול וקטורי ה-X













