חידה מתמטית
חידה מתמטית היא חידה שפתרונה מצריך יכולת מתמטית ושימוש בכלים מתמטיים.
הספר הידוע הראשון שנושאו חידות מתמטיות הוא ספרו של קלוד באשה, Problèmes plaisans et délectables, שיצא לאור בצרפת בשנת 1612. בעבר החידות המתמטיות, במובן בעיות מתמטיות שעוסקות במקרה פרטי במקום בעיקרון הכללי, היו מרכז המתמטיקה בתרבויות מסוימות.
הגבול בין חידה מתמטית לבין בעיה מתמטית אינו חד וברור, ולעיתים משמשת החידה להמחשה של בעיה כללית יותר. מאפיינים להבחנה בין חידה מתמטית לבעיה מתמטית:
- חידה מוצגת בצורה של סיפור מעשה, בעוד שבעיה מנוסחת בצורה טכנית-פורמלית.
- חידה עוסקת במקרה פרטי, בעוד שהבעיה המקבילה לה עוסקת בחקירת המקרה הכללי. דוגמה להבדל זה מוצגת בבעיית יוספוס.
- חידה מצריכה פתרון אד-הוק, כזה שיפה לחידה זו בלבד, ואילו לבעיה יש פתרון שבלוני, במסגרת רחבה יותר.
חידה מתמטית נראית לעיתים כחידה רק עקב ניסוחה המיוחד או משום שהיא מתבססת על ידע שחסר לנשאל. החידה "בקבוק בלי פקק עולה 20 שקלים יותר מהפקק, ושניהם יחד (הבקבוק והפקק) עולים 21 שקלים - מה מחיר הבקבוק?", היא בפירוש חידה כאשר היא מוצגת לילד, אך מי שלמד אלגברה יזהה בה מיד בעיה פשוטה בנעלם אחד או בשני נעלמים.
חידות מתמטיות נודעות[עריכת קוד מקור | עריכה]
כיום החידות משמשות ללימוד המתמטיקה, להדגמתה ולשעשוע, אולם בעבר הן הוצגו בספרי המתמטיקה החשובים ביותר. המתמטיקה המצרית העתיקה, הבבלית והסינית התבססו במידה רבה על חידות ופתרונן (ראו הרחבה בערך היסטוריה של המתמטיקה). לדוגמה, הספר תשעת הפרקים של אמנות המתמטיקה, אחד הספרים המשפיעים ביותר היסטוריה של המתמטיקה, מורכב כל כולו מחידות מעשיות, מהן ניתן ללמוד על עקרונות התחום. כדוגמה אפשר להביא את בעיה 26 מהפרק החמישי בספר, שחידות מסוגה נפוצות עד ימינו, אך רק כאתגר ללומדי מתמטיקה ברמת בית הספר:
מקווה מוזן על ידי חמש תעלות. דרך התעלה הראשונה לבדה יוזן המקווה בשליש יום, דרך השנייה לבדה ביום, דרך השלישית לבדה ביומיים וחצי, דרך הרביעית לבדה בשלושה ימים ודרך החמישית לבדה בחמישה ימים. לו תחוברנה כל התעלות בו-זמנית למקווה, כמה זמן ייקח לו להתמלא?[1]
— "תשעה פרקים של אמנות המתמטיקה"
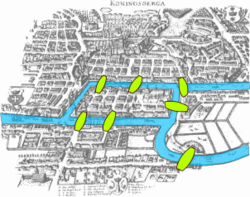
חידה מפורסמת במיוחד מספרת על הגשרים של קניגסברג. תושביה של העיר קניגסברג האמינו שלא ניתן לחצות את כל שבעת הגשרים בעיר ולחצות לנקודת המוצא מבלי לחצות גשר כלשהו יותר מפעם אחת. לאונרד אוילר פתר את החידה העממית הזאת בעזרת תיאור סכמטי של הגשרים, והבין מהם המקרים (מבחינת מספר הגשרים ומיקומם) בהם משימה כזו תהיה אפשרית, דבר שהיווה פריצת דרך עצומה בתורת הגרפים.
חידות מפורסמות נוספות:
ספרי חידות מתמטיות[עריכת קוד מקור | עריכה]
- אמיל פוירשטין, יגעת ומצאת, הוצאת א. זלקוביץ, 1976.
- משה ד. כספי, מי חושב?, הוצאת מסדה, 1978.
- בן-ציון ארז, לתפוס ראש, הוצאת תמר, 1983.
- עמי בירנבוים, מספר חזק, הוצאת תמר, 1996.
- דייוויד וולס, ספר החידות הגדול, הוצאת מי-אן, 1998.
- יורי צ'רניאק ורוברט רוז, התרנגולת ממינסק, הוצאת אחיאסף, 1999.
- כפיר כהן, אוסף החידות הגדול, הוצאת רקפת, 2001.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- אתרי חידות מתמטיות בעברית
- דוד שי, המשפט האחרון של פרמה - חידות מתמטיות
- אלף אפס - חידות
- סבינה סגרה, המעגל המתמטי, במדור "מאגר המדע" באתר של מכון דוידסון לחינוך מדעי, 24 פברואר 2008 (הקישור אינו פעיל)
- חידה מתמטית, באתר MathWorld (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ הפתרון לשאלה זו הוא ימים. הוכחת הפתרון: נגדיר את ההספק P של כל צינור כך שה"עבודה" W תמדד ביחידות של "מקווה" והזמן t ביחידות "יום". כיוון שהעבודה קבועה עבור כל צינור ושווה למקווה אחד, הספקו של כל צינור יהיה הגודל ההופכי לזמן בו לוקח לו להתמלא. כך, הספקו של הצינור הראשון ביחידות מקווה/יום יהיה 3, השני 1, השלישי 2/5, הרביעי שליש והחמישי חמישית. כאשר כולם מחוברים ביחד מתקבלת, על ידי ההגדרה , המשוואה הבאה:. תוצאת המשוואה היא .





